引入名词

首先引入几个名词。

BP神经网络

BP（Back Propagation）网络是1986年由Rumelhart和McClelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断调整网络的权值和阈值，使网络的误差平方和最小。BP神经网络模型拓扑结构包括输入层（input）、隐层(hide layer)和输出层(output layer)。

简单的来说，

BP的传播对象就是“误差”，传播目的就是得到所有层的估计误差。

它的学习规则是：使用梯度下降法，通过反向传播（就是一层一层往前传）不断调整网络的权值和阈值，最后使全局误差系数最小。

NaN

NaN（Not a Number，非数）是计算机科学中数值数据类型的一类值，表示未定义或不可表示的值。常在浮点数运算中使用。首次引入NaN的是1985年的IEEE 754浮点数标准。

独热码

独热码，在英文文献中称做 one-hot code, 直观来说就是有多少个状态就有多少比特，而且只有一个比特为1，其他全为0的一种码制。通常，在通信网络协议栈中，使用八位或者十六位状态的独热码，且系统占用其中一个状态码，余下的可以供用户使用。

Nabla算子

向量微分算子，Nabla算子（nabla operator），又称劈形算子，倒三角算子，哈密顿算子，是一个微分算子。

当应用于在一维域上定义的函数时，它表示其在微积分中定义的标准导数。 当应用于场（在多维域上定义的函数）时，del可以表示标量场（或者有时是矢量场，如在Navier-Stokes方程式中）的斜率（局部最陡坡度），发散度的矢量场，或矢量场的旋度（旋转），这取决于它的应用方式。

严格来说，del并不是一个特定的算子，而是一个方便的使用的数学符号，这使得许多方程易于书写和记忆。nabla算符可以解释为向量的偏导数运算符，其三个可能的含义 - 梯度，散度和旋度 - 可以被正式地视为具有标量，点积和交叉乘积的乘积。详细描述如下 [1] ：
梯度：

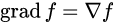
散度：

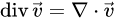
旋度：

---

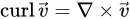
1神经网络

1.1 神经元模型

神经元模型是模拟生物神经元结构而被设计出来的。典型的神经元结构如下图1所示：
神经元大致可以分为树突、突触、细胞体和轴突。

树突为神经元的输入通道，其功能是将其它神经元的动作电位传递至细胞体。其它神经元的动作电位借由位于树突分支上的多个突触传递至树突上。神经细胞可以视为有两种状态的机器，激活时为“是”，不激活时为“否”。神经细胞的状态取决于从其他神经细胞接收到的信号量，以及突触的性质（抑制或加强）。当信号量超过某个阈值时，细胞体就会被激活，产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。（内容来自维基百科“感知机”）

同理，神经元模型就是为了模拟上述过程，典型的神经元模型如下：

这个模型中，每个神经元都接受来自其它神经元的输入信号，每个信号都通过一个带有权重的连接传递，神经元把这些信号加起来得到一个总输入值，然后将总输入值与神经元的阈值进行对比（模拟阈值电位），然后通过一个“激活函数”处理得到最终的输出（模拟细胞的激活），这个输出又会作为之后神经元的输入一层一层传递下去。

1.2 神经元激活函数

激活函数(Activation functions)，将非线性特性引入到网络中。如下图，在神经元中，输入的 inputs 通过加权，求和后，还被作用了一个函数，这个函数就是激活函数。

引入激活函数是为了增加神经网络模型的非线性。没有激活函数的每层都相当于矩阵相乘。就算你叠加了若干层之后，无非还是个矩阵相乘罢了。

1.2.1 为什么要使用激活函数？

• 激活函数对模型学习、理解非常复杂和非线性的函数具有重要作用。
• 激活函数可以引入非线性因素。如果不使用激活函数，则输出信号仅是一个简单的线性函数。线性函数一个一级多项式，线性方程的复杂度有限，从数据中学习复杂函数映射的能力很小。没有激活函数，神经网络将无法学习和模拟其他复杂类型的数据，例如图像、视频、音频、语音等。
• 激活函数可以把当前特征空间通过一定的线性映射转换到另一个空间，让数据能够更好的被分类。

1.2.2为什么激活函数需要非线性函数？

• 假若网络中全部是线性部件，那么线性的组合还是线性，与单独一个线性分类器无异。这样就做不到用非线性来逼近任意函数。
• 使用非线性激活函数 ，以便使网络更加强大，增加它的能力，使它可以学习复杂的事物，复杂的表单数据，以及表示输入输出之间非线性的复杂的任意函数映射。使用非线性激活函数，能够从输入输出之间生成非线性映射。

1.2.3常用的激活函数

• sigmoid 激活函数

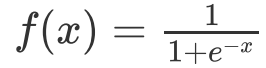
其值域为 (0,1) 。函数图像：

• 特点：

能够把输入的连续实值变换为0和1之间的输出，特别的，如果是非常大的负数，那么输出就是0；如果是非常大的正数，输出就是1.

• 缺点：
  • sigmoid函数曾经被使用的很多，近年来，用它的人越来越少了。主要是因为它固有的一些缺点。
• 缺点1：
  • 在深度神经网络中梯度反向传递时导致梯度爆炸和梯度消失，其中梯度爆炸发生的概率非常小，而梯度消失发生的概率比较大。首先来看Sigmoid函数的导数，如下图所示：

• 缺点2：
  • 不是以0为对称轴（这点在tahn函数有所改善）

• tanh激活函数

tanh读作Hyperbolic Tangent，它解决了Sigmoid函数的不是zero-centered输出问题，然而，梯度消失（gradient vanishing）的问题和幂运算的问题仍然存在。

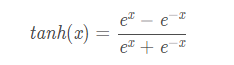
其值域为 (-1,1) 。函数图像：

导数：$f^{\prime }(x)=1-(f(x){)}^2$
导函数图像：
优点和缺点

• 优点：
• 解决了Sigmoid的输出不关于零点对称的问题
• 也具有Sigmoid的优点平滑，容易求导
• 缺点： 激活函数运算量大（包含幂的运算）
• Tanh的导数图像虽然最大之变大，使得梯度消失的问题得到一定的缓解，但是不能根本解决这个问题

• Relu激活函数

它保留了 step 函数的生物学启发（只有输入超出阈值时神经元才激活），不过当输入为正的时候，导数不为零，从而允许基于梯度的学习（尽管在 x=0 的时候，导数是未定义的）。使用这个函数能使计算变得很快，因为无论是函数还是其导数都不包含复杂的数学运算。然而，当输入为负值的时候，ReLU 的学习速度可能会变得很慢，甚至使神经元直接无效，因为此时输入小于零而梯度为零，从而其权重无法得到更新，在剩下的训练过程中会一直保持静默。函数的定义为：$f(x)=max(0,x)$,值阈$[0,+\infty ]$。函数图像如下：

导数：

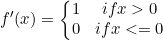
导函数图像：

• 优点：

  • 相比起Sigmoid和tanh，ReLU在SGD中能够快速收敛，这是因为它线性（linear）、非饱和（non-saturating）的形式。

  • Sigmoid和tanh涉及了很多很expensive的操作（比如指数），ReLU可以更加简单的实现。

  • 有效缓解了梯度消失的问题。

  • 在没有无监督预训练的时候也能有较好的表现。

• 缺点：
  • ReLU的输出不是zero-centered
  • Dead ReLU Problem，指的是某些神经元可能永远不会被激活，导致相应的参数永远不能被更新。有两个主要原因可能导致这种情况产生:
    (1) 非常不幸的参数初始化，这种情况比较少见 (2) learning
    rate太高导致在训练过程中参数更新太大，不幸使网络进入这种状态。解决方法是可以采用Xavier初始化方法，以及避免将learning
    rate设置太大或使用adagrad等自动调节learning rate的算法。
    尽管存在这两个问题，ReLU目前仍是最常用的activation function，在搭建人工神经网络的时候推荐优先尝试！

1.3 神经网络结构

http://t.cn/RBCoWof
使用如下神经网络结构来进行介绍，第0层是输入层（3个神经元）， 第1层是隐含层（2个神经元），第2层是输出层：

每一列都表示一个样本，从样本1到m
$w^l$的含义和原来完全一样，$Z^l$也会变成m列，每一列表示一个样本的计算结果。

2.损失函数和代价函数

损失函数（Loss Function）和代价函数（Cost Function）并没有一个公认的区分标准。

损失函数主要指的是对于单个样本的损失或误差；代价函数表示多样本同时输入模型的时候总体的误差——每个样本误差的和然后取平均值。

3.反向传播

反向传播链接
详细过程链接

参考：
https://zhuanlan.zhihu.com/p/38006693
https://www.jianshu.com/p/67393ddc2af2
https://blog.csdn.net/u014303046/article/details/78200010
https://www.sohu.com/a/235924191_633698
https://blog.csdn.net/ft_sunshine/article/details/90221691