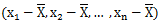转自: http://www.d2school.com/bhcpp_book/5_8.php
5.8.1 十六进制
说到十六进制,首先会问:总共只有10个阿拉伯数字:0、1、2、3、4、5、6、7、8、9,如何表达“逢16进1”的概念呢?方法是用英文字母(大小写均可):A、B、C、D、E、F表达10~15。所以,如果我告诉你:这是一个数:“17FCA0”,你肯定能猜到它是一个十六进制的数,不过如果我说的是:“12390”,就不好区分是什么进制了。
在C++语言中,并不支持直接在代码中写一个2进制数(后面谈为什么),但倒是支持直接写一个十六进制的数,为了能和十进制数区分,C++规定十六进制数需要一个前缀:“0x”(数字0和小写字母x),比如:
int a = 0x17FCA0;
为什么已经有十进制数了,还要再搞出个十六进制数呢?是不是现实生活中有这个需求,比如有什么东西的计数特别适合用“十六进制”呢?生活中确实不仅仅只有十进制。比如“袜子”就很像二进制计数:没有袜子是0只袜子,1只袜子是1只袜子,2只袜子……逢二进一:成1双袜子,果然只需要0和1。
〖小提示〗:生活中的各种进制
时间是60进制,角度也是60进制。说到“一打东西”时,用的是12进制。请各位课后可以想想还有什么进制。
其实十六进制的存在,纯粹是为了二进制。二进制是肯定必定以及一定要存在的,因为机器用的就它。但二进制数实在太“占位置”了,虽然最直观,但读写都不方便。如果用十进制呢——当然,编程序我们最常用还是十进制,仅当要需要表达和机器相关的数据,一些内存地址时,才会考虑二进制——十进制数和二进制转换比较复杂,十六进制就不一样了,它和二进制的之间的转换非常简单快速。
一个数用二进制表达,实际就是由多个“2的N次方的数”相加。因为16是2的4次方,因此非常这两个进制之间的转换特别容易(想想10是2的几次方呢?)。
或许还会问:还有很多数是2的整数次乘方啊,比如8是2的3次方,32是2的5次方,为什么偏偏是16呢?原来。一个字节(byte)是8位,但用“2的8次方”作为进制,显然太大了。另外,我们还会有把一个字节分为“高字节(高4位)”和“低字节(低4位”的需要,所以,用16(2的4次方)来作为进制最方便。说千道万,试一试会更清楚些:下面就让我们做一些二进制数与十六进制数的互换运算。
- 二进制数 -> 十六进制数
我们首将就以“半个字节(4位)”为例,看看4位的二进制数如何转换成十六进制。因为是刚开始,所以我们先保留转换到十进制的中间步骤,但慢慢的,我们要学会直接转换。
1000(2) => 8+0+0+0 = 8 => 0x8
1001(2) => 8+0+0+1 = 9 => 0x9
1010(2) => 8+0+2+0 = 10 => 0xA
1111(2) => 8+4+2+1 = 15 => 0xF
最后一个例子最说明问题:转换二进制数,请以4位为一组,然后从高位看到低位,各位的权值依次是:“8、4、2、1”。如果该位是1,就加上权值,否则不加,就可以得到一个十进制数,然后再快速换算成十六进制(要求你熟记A~F对应的十进制值)。
真正能体现十六进制的方便,在于位数更多时,比如当面对一个完整的一个字节时,比如(为了不引起眼花,我们每4位加一个空格): 0101 1110。这个二进制数如何转换成十六进制呢?
第一种方法:转换成十进制数,再转换为十六进制:
先换算成十六进制:0101 1110 = 0 + (2的6次方) + 0 + (2的4次方) + (2的3次方) + (2的2次方) + (2的1次方:2) + 0 = 94。
还得把十进制的94换算成十六进制,如何算?我们还没教呢,这里先给出答案:94 = 0x5E。
![]() 〖课堂作业〗:体验二进制数换算至10进制的“笨方法”
〖课堂作业〗:体验二进制数换算至10进制的“笨方法”
请拿起笔,立即用以上方法中步骤一,将以下二进制数换算成十进制数:
8位数:11011100、01110110、10010101、11011101;
16位数:1101101000110101
第二种方法:每4位直接换算成十六进制数,得到的就是结果:
高4位:0101(2) -> 4+1 -> 0x5
低4位:1110(2) -> 8+4+2 -> 0xE
结果就是:0x5E。
来一个难点的:16位的二进制数:1101101000110101,如何换算成十六进制呢?
首先,每4位拆成一组:1101 1010 0011 0101
1101 -> 13 -> 0xE
1010 -> 10 -> 0xA
0011 -> 0x3
0101 -> 0x6
结果就是:0xEA36。
- 十六进制数 -> 二进制数
十六进制数的换算成二进制数,也有两种方法,不过我们直接学习“聪明”的方法, “笨”的方法,留到后面“进制换算”时再提。
前面给出“8、4、2、1”口诀,现在只需要学会给出一个16以内的数,你能拼出它的二进制数即可,比如:
0xA -> 10 = 8 + 2 -> 1010(2)
0xD -> 13 = 8 + 4 + 1 -> 1101(2)
0xF -> 15 = 8 + 4 + 2 + 1 -> 1111(2)
再如:
0xC9D5 要换算成进二进制,类似:
0xC -> 12 = 8 + 4 -> 1100(2)
0x9 -> 8 + 1 -> 1001(2)
0xD -> 1101(2)
0x5 -> 4 + 1 -> 0101
结果是:11001001 11010101。请特别注意最后0x5的转换,不足4位,前面补0。
有关十六进制的内容,我们就一直讲它如何与二进制制互换?没错,因为在我们编程时,我们绝大多数要把十六进制就当成是二进制的一个马甲——二进制数穿上这马甲,图的就是让人类看起来舒服一些,仅此而已。
5.8.2. 八进制
八进制,二进制的另一个小尺寸的马甲。不过我们用得并不多。关于它,首先要说的就是:在C++程序中,当一个数字以0开始时,它就是八进制。这是一件不太直观的事情。
int a = 010; //对不起,这不是4,也不是10,它是8。
八进制,使用了0~7这8个阿拉伯数字。逢8则进1,所以看到八进制的“10”,你应该可以换算出它其实是一个十进制的8。八进制各位的权值,以8为基数。下面的算式演示了八进制的173如何换算成十进制的123。
173(8) -> 1×(8的2次方:64) + 7×(8的1次方:8) + 3 -> 123(10)
我们再看看:一个二进数,如何换成八进制:“11101111” 是一个8位的二进制数。我们从低位往高位,每三位分一组(想想,为什么是每三位),得到:11、101、111,然后每仿效换成十进制(但3位的二进制数,肯定不会超过7,所以,说是换算成八进制,或许更好理解):
11(2)-> 3
101(2) -> 5
111(2) -> 7
结果是:357(8)。
八进制数换算成二进制数,应该是张口就来。请熟记八进制数,每个数的二进制值:
| 7 -> 111(2) | 3 -> 011(2) |
| 6 -> 110(2) | 2 -> 010(2) |
| 5 -> 101(2) | 1 -> 001(2) |
| 4 -> 100(2) | 0 000(2) |
(表格 4 八进制数与二进制数速换表)
或许,你头脑里闪现出一个,八进制数与十六进制数互换的方法了,没有吗?
5.8.3. 进制换算
先说一下前小节的答案吧。八进制数与十六进制数互换的方法之一,就是用二进制做桥梁。
以下是我们已经学会的换算过程:
二进制 -> 八进制、十六进制
十六进制、八进制 -> 二进制
二进制、八进制、十六进制 -> 十进制
本节我们主要学习,十进制数,如何换算成其它进制,它们都有一个统一的方法,称为“连除法”。
- 十进制数 -> 二进制数
将十进制数除以2,得到商和余数,将商再除以2,直到商为0;然后将本过程中得到的余数(肯定不是0就是1),先得到的排后边,后得到的排前边,就是结果了。
例子:将6换算成二进制数:
| 表达式 | 商 | 余数 |
| 6÷2 | 3 | 0 |
| 3÷2 | 1 | 1 |
| 1÷2 | 0 | 1 |
表格 5 十进制数6换算成二进制过程表
将余数按得到的先后,倒序排列,得到“110”,正是6的二进制表达。
如果要应付考试,慢腾腾地画上面那张表,显然会急死人,所以通常是在草稿纸上如下图所示进行演算:
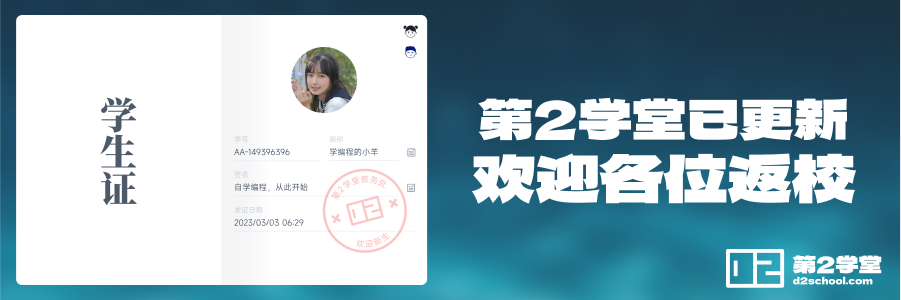
图 5-22 连除法演算过程草图
- 十进制数 -> 八进制数
方法类似换算成二进制数,只不过除数变成8。
例子:将289换算成八进制数:
| 表达式 | 商 | 余数 |
| 289÷8 | 36 | 1 |
| 36÷8 | 4 | 4 |
| 4÷8 | 0 | 4 |
表格 5-6 十进制转八进制示例
将余数按得到的先后,倒序排列,得到“441”,正是289的八进制表达。
- 十进制数 -> 十六进制数
方法类似换算成二进制数,只不过除数变成16。
例子:将872换算成十六进制数:
| 表达式 | 商 | 余数 |
| 874÷16 | 36 | 1 |
| 54÷16 | 4 | 4 |
| 3÷16 | 0 | 4 |
表格 5-7 十进制转十六进制示例
将余数按得到的先后,倒序排列,得到“0x36A”,正是874的十六进制表达。
5.8.4. 浮点数
在C++程序中,以“位”的形式访问一个整数(尤其是无符号整数),比较常见,比如“位移”操作(将一个二进制数中的每一位,同时向左向右移动若干位)、或者按位“与”、“或”、“异或”等。但我们很少对一个“非整数”进行此类操作。
“浮点数/floating point numbers”是计算机用来“近似”表达实数的一种方法。中学时学习的“科学计数法”,就有点类似。另外,并不能将“浮点数”和“N进制”二者可以是表达同一个数的两上不同切入点,换句话说,存在十进制的浮点数,也存在二进制的浮点数。要不,我们就来看一个十进制数的浮点表示法:
9.57 × (10的2次方)
这个数是什么?其实它就是实数“957.0”的浮点表示法。
一个规范的“浮点数”表达方式,需要满足如下特征.
表达式:d.dd...d × (B 的 e 次方)。
其中,d.dd...d 称为“尾数”(更通俗的说法是:“有效数字”),B 称为“基数”,e称为“指数”。
对于不同进制,则首先表现在B的值,B是2,就是二进制,是10,就是十进制。当然,“尾数”中每一个d的取值范围,也要随进制变化而变,当为十进制数,d就是0~9,为二进制数时,d就只能是0~1。
再者,“尾数”中的整数部分(即小数点的左部),不能为0。因此,类似下面的数,它们都不是规范的浮点数:
10.123 × (10的2次方)
2.0101 × (2的3次方)
0.0134 × (10的-1次方)
![]() 〖课堂作业〗:浮点数的规范表达
〖课堂作业〗:浮点数的规范表达
请指出三个浮点数表达式的错误,并以正确方式写出(数值大小必须保持一致)。
如果明确使用二进制表达的话,则是:d.dd...d × (2 的 e 次方)。其中每一位d都只能是0或1,同样,整数部分不能是0。
第一个规范的浮点数,都可以通过以下表达式计算得到:
±(d0 + d1×(B的-1次方) + d2×(B的-2次方) + d3×(B的-3次方) + ... + dn×(B的-n次方))×(B的e次方)
别被这个长长和式子吓倒!它不过是让我们回想起小学时光而已。我们举一个例子,假设有一个十进制的浮点数:3.456×(10的3次方)
我用“0.1”表示“10的-1次方”,则有:
则有:3.456 = 3 + 4×0.1 + 5×0.01 + 6×0.001
所以:3.456×(10的3次方) = (3 + 4×0.1 + 5×0.01 + 6×0.001)×(10的3次方)。
没错,小学时,我们都会念:“小数点之后第一位,表示0.1,第二位,表示0.01,第三位,表示0.001……”那二进制呢?假设也用最直观的方式表示一个带小数的二进制:
1111.1111
2的0次方(=0),1次方(=1),2次方(=4),3次方(=8)……
小数点往右,则是——
2的-1次方(=0.5),-2次方(=0.25),-3次方(0.125)、-4次方(=0.0625)……
![]() 〖课堂作业〗:0.1 如何表达?
〖课堂作业〗:0.1 如何表达?
不需要写出“尾数”、“指数”,请以前述内容为例,请尝试写出十进制数0.1的小数部分,如何二进制表达:0.000______。
显然,小数点后面三位,必须都为0,因为它们权值,都比0.1大,然后大概可以这样拼凑:
首先我们让2的-4次方,加上2的-5次方:
0.0625 + 0.03125 = 0.09375。
很接近了,但后面不能再加上2的-6次方(0.015625),加上就超出0.1了,加2的-7次方(0.0078125)也不行……加上2的-8次方(0.00390625),得到0.09765625,越发逼近,但它终究还不是0.1。没关系,这样一直拼凑下去,或许就能刚好凑出一个0.1。如果一直凑不出来呢?也没关系嘛,让我们用上高中的数学知识,假如允许我们这样无限地——注意,是无限地——凑下去,那么什么数都可以逼近逼近,直到在数学被认为相等。
〖小提示〗:0.9999999…… 等于1吗?
高中在学习“极限”时,数学老师一定告诉过你了,当0.9999……后面有无穷尽个9时,那么0.9999999……就等于1。
可惜,“极限”存在于数学世界中,在现实中,计算机的内存容量不仅不是“无穷尽”的,而且是宝贵的,所以,再说一次:“浮点数是计算机用来‘近似’表达实数的一种方法”。如果以四个字节来存储,那么总共才32位。
当然,似乎也并不是所有数字,都无法精确地用浮点表达,比如,0.5,那就是2的-1次方,非常精确。但是,这也只是说,你直接在代码里,写一个0.5时,它是精确的,如果它是通过一个“算式”计算得到,而该算式中又存在一些个无法精确表达的浮点数,比如:0.01×10.0÷0.2,谁也不好保证,它能在计算机中得到一个精确的0.5。这就是比较浮点数时,所需要注意的精度问题,请看下面代码:
if (0.01f * 10.0f / 0.2f == 0.5f){cout << "yes!" << endl;}else{cout << "no." << endl;}
C++程序用*代表乘号,/代表除号。而“0.01f”末尾的f,表示这是一个单精度的浮点数。上面程序运行时,将输出“no.”。也就是说,此时“0.01×10.0÷0.2”并不等于0.5。这种问题如何解决呢?我们并不急于在此处提出答案,重要的是,你必须记住这一问题,并理解它的原因。
〖小提示〗:计算机不可信了吗?
曾经有学生问我,我一直以为,计算机计算比人类精确多了,可是今天看起来计算机的计算也很不可信啊?连小学生都会的题,它也能算错?放心吧,尽管浮点数不精确,但它也是一种“非常精确的不精确”,问题完全可溯可查可解决。另外,我看到一些不知其所以然的程序员,认为写一个这样的判断: “if (0.1 == 0.1) ...”,也要担心个半天,放心吧,如果这样的判断出错,那计算机真的可以扔了。
计算机通常提供两种精度的浮点数表达方法,其中一种不太精确,另一种则更不精确——噢,这样说有点消极,重来:“其中一种不太精确,另一种则比较精确。”。不太精确的,就是“单精度浮点数”,比较精确的,就是“双精度浮点数”。
- 单精度浮点数
C++用float类型表示单精度浮点数。它占用4个字节,合32位。其中符号、指数、尾数各自占用的位域如下图所示:
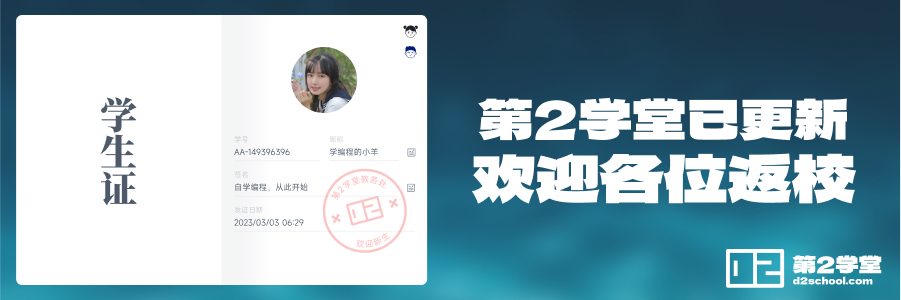
图 5-23 单精度浮点数位域
如果代码中写一个字面常量的浮点数,需要在数字尾部,加上字母f,比如:0.1f,或10f,默认情况下,C++将字面上的一个带小数字,当成双精度浮点数。
- 双精度浮点数
C++用double类型表示双精度浮点数。它占用8个字节,合64位。其中符号、指数、尾数各自占用的位域如下图所示:
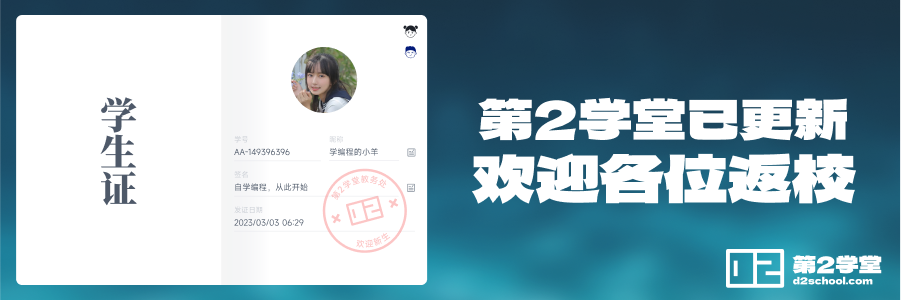
图 5-24 双精度浮点数位域
当在代码中写一个数字,如果不带小数,则默认是整型数,比如:10,如果加上小数点,比如:10.0,并且没有尾随字母f,则C++将之当成double类型。
以上并不是有关浮点数表达的全部知识,要表达一个浮点数,还需要很多约定。考虑到编写C++程序时,我们只会(也只允许)对整数类型(包括int, long, char等)的数据进行按位操作,浮点数的基础知识,我们暂时只讲到这里。
![]() 〖课堂作业〗:浮点数精度练习
〖课堂作业〗:浮点数精度练习
请将前述有关“0.01×10.0÷0.2”判断是否等于0.5代码,写成一个控制台测试项目。并且分别针对float类型和double类型进行测试,看看结果是否有区别。