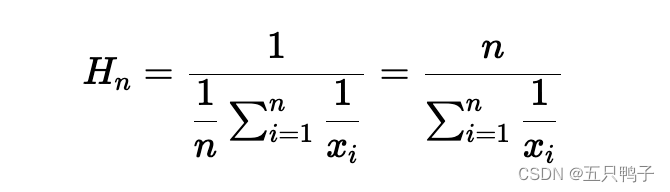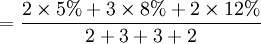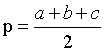本文内容

• 算术平均
• 几何平均
• 调和平均
• 平方平均
• 移动平均

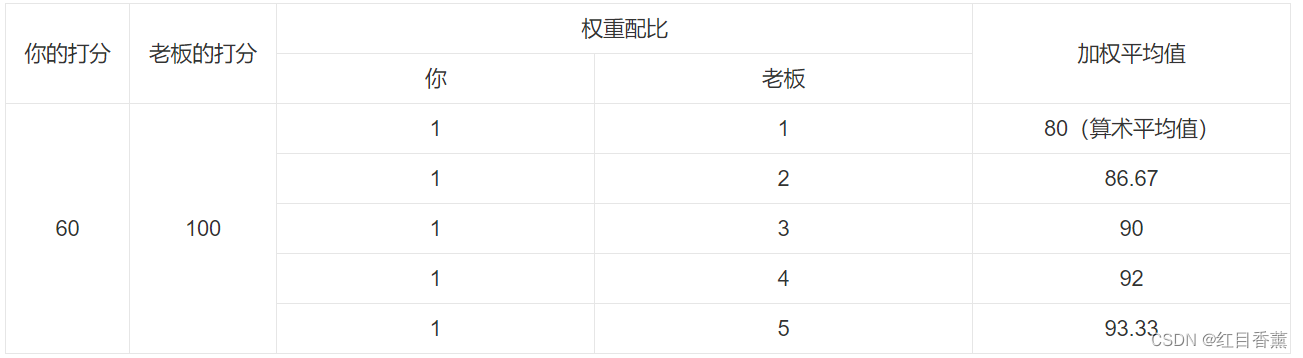
算术平均、几何平均、调和平均、平方平均和移动平均跟计算编程有什么关系：Just One Word，不能只会算术平均数，还有其他很多选择，以及不同场景使用不同的平均数。

算术平均

---

算术平均（Arithmetic mean）是最基本、最常用的一种平均指标，描述数据集中趋势的一个统计指标。

计算公式为：

即，n 个数据相加后除以 n。0 也记入。

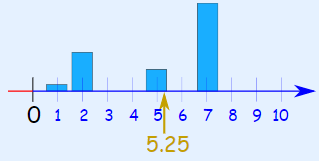
统计学上，算术平均较中位数和众数更少受到随机因素影响， 但缺点是它极易受到极大极小值的影响。例如，有数组 (5, 7, 5, 4, 6, 7, 8, 5, 4, 7, 8, 6, 20)，平均值是 7.1，但实际上大部分数据（10个）都不超过7，如果去掉 20，平均数为 6。

上面是简单算术平均，它只是加权算术平均的一种特殊形式。若原始数据，被分成 k 组，各组的值为 (x1，x2，...，xk)，各组频率分别为 (f1，f2，...，fk)，则加权算术平均数的计算公式为：

由公式可以看出，加权算术平均数同时受到两个因素的影响，一个是各组数值的大小 xi，另一个是各组分布频数 fi。在数值不变的情况下，某组的频数越多，该组数值对平均数的作用就大，反之，越小。

算术平均可以用来反映一组数据的一般情况，也可以对不同组的数据进行比较。平均数可以直观、简明的表示一组数据，所以，在日常生活中经常用到，如平均速度、平均身高、平均产量、平均成绩等等。算术平均主要适用于数值型数据，不适用于品质数据。

几何平均

---

几何平均（Geometric mean），是另一种计算平均值的方法。对几何平均，也可以像算术平均一样，做加权的几何平均。

简单几何平均的计算公式为：

即，n 个数据相乘后开 n 次方。其中，xi 都是正实数。

几何平均适用于对比率、指数等进行平均，主要用于平均增长（变化）率，对数正态分布。

算术-几何平均数

若有两个正实数 x 和 y，则它们的算术-几何平均数为，先计算这两个数的算术平均数，称为 a1；再计算它们的几何平均数，称为 g1。

重复这个步骤，便得到了两个数列 (an) 和 (gn)：

这两个数列都收敛于一个相同的数，这个数称为 x 和 y 的算术-几何平均数，记为 M(x, y) 或 agm(x, y)。

示例：

• 计算 a0 = 24和 g0 = 6的算术-几何平均数 M(24, 6) 如下表所示：

 

n	an	gn
0	24	6
1	15	21
2	13.5	13.41640786500...
3	13.45820393250...	13.45813903099...
4	13.45817148175...	13.45817148171...

 

a0 = 24和 g0 = 6的算术-几何平均数  。

• 1 和 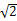 的算术-几何平均数的倒数，称为高斯常数。

调和平均

---

调和平均（Harmonic Mean），也分简单和加权的形式。加权调和平均数是加权算术平均数的变形。多数多情况下，我们只掌握每组某个标志的数值总和（m），而缺少总体单位数（f）的资料，因此，不能直接采用加权算术平均数法计算平均数，而则采用加权调和平均数。

先由加权算术平均数公式推到加权调和平均公式，最后推到简单调和平均公式，它是加权调和公式的特殊形式。加权算术平均的计算公式为：

即，加权调和平均公式为：

当 mi=1 时，则公式退化成简单调和平均公式：

即，n 个数据的倒数取算术平均，再取倒数。

调和平均一般用于计算平均速率。

示例：某工厂购进材料三批，每批价格及采购金额资料如下表：

	价格x（元/千克）	采购金额 m（元）	采购数量 m/x（千克）
第一批	35	10000	286
第二批	40	20000	500
第三批	45	15000	330
合计	——	45000	1116

 

 

每千克 40.32 元。

二个数的调和平均数

最常用的是二个正数值 x1 和 x2 的调和平均数 H：

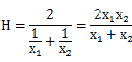
而 x1 和 x2 的算术平均数 A 与几何平均数 G 分别为：

那么，它们存在如下关系：

应用

• 可以用在相同距离，但速度不同的平均速度，如一段路，前半段时速 60 公里，后半段时速 30 公里〔两段距离相等〕，则其平均速度为两者的调和平均数 40 公里。

• 两个电阻 R1 和 R2 并联后的等效电阻 Req 为调和平均数的一半。

• 物理学中的减缩质量也为调和平均数的一半。

毕达哥拉斯平均是算术平均数（A）、几何平均数（G）及调和平均数（H），这三种平均数的总称。

平方平均

---

平方平均（Quadratic mean），简称方均根（Root Mean Square，RMS），是平方根的广义平均（generalized mean），计算公式为：

即，n 个数据的平方取算数平均，再开平方根。

利用柯西不等式，平方平均与算术平均的关系是：平方平均不小于算术平均。

应用

• 平方平均数常用来计算一组数据和某个数据的“平均差”。像交流电的电压、电流数值以及均匀加速直线运动的位移中点平均速度，都是以其实际数值的方均根表示。例如，交流电 220V 表示电压信号的均方根（又称为有效值），即 220V，为交流电瞬时值（瞬时值又称暂态值）的最大值的。
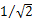• 统计中的标准差 s：

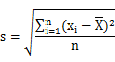
即，所有数据  与算术平均值  相减 ，取它们的平方平均数。

移动平均

---

移动平均（Moving Average，MA），又称“移动平均线”简称均线，是一种简单平滑预测技术，它的基本思想是：根据时间序列资料、逐项推移，依次计算包含一定项数的序时平均值，以反映长期趋势的方法。因此，当时间序列的数值由于受周期变动和随机波动的影响，起伏较大，不易显示出事件的发展趋势时，使用移动平均法可以消除这些因素的影响，显示出事件的发展方向与趋势（即趋势线），然后依趋势线分析预测序列的长期趋势。

移动平均法适用于即期预测。当产品需求既不快速增长也不快速下降，且不存在季节性因素时，移动平均法能有效地消除预测中的随机波动，是非常有用的。移动平均可抚平短期波动，反映出长期趋势或周期。最常见的是利用股价、回报或交易量等变量计算出移动平均。

数学上，移动平均可视为一种卷积（卷积是通过两个函数 f 和 g 生成第三个函数的一种数学算子，表征函数 f 与经过翻转和平移的 g 的重叠部分的累积。如果将参加卷积的一个函数看作区间的指示函数，卷积还可以被看作是“移动平均”的推广）。

移动平均法可以分为：简单移动平均和加权移动平均。

参考地址：https://www.cnblogs.com/liuning8023/p/3525920.html