“ RFM分析,是用户精细化运营中比较常见的分析方法了。”
今天和大家分享一篇历史文章,内容做了微调。是数据分析中比较常用的一个分析框架:RFM分析。该模型用的很多,说明有模型自身的优势;但同时也存在很多的问题。今天和大家一起探讨。
01
—
什么是RFM分析
RFM分析,其实是一种将用户分层、进而针对不同用户群体进行精细化运营的方法。
RFM的三个字母,分别代表了一个维度:
R(Recency):最近一次消费时间。反映了用户最近消费的热度,用以衡量用户是否流失。理论上,最近一次消费时间越长,流失概率越高
F(Frequency):用户的消费频率。反映了用户对于产品、品牌的忠诚程度。理论上,一定时间内的购买频率越高,用户忠诚度越高
M(Monetary):消费金额。反映了用户的购买力。
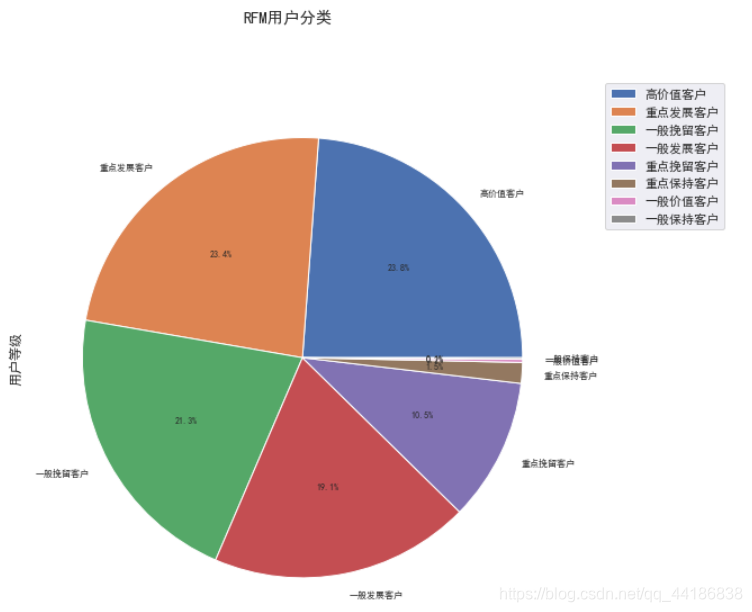
通常来讲,是针对每个维度设定一个阈值,将用户群体划分为二(高于阈值、低于阈值),三个维度齐下,则可以将用户整体划分为2^3=8个用户细分群。如下图:
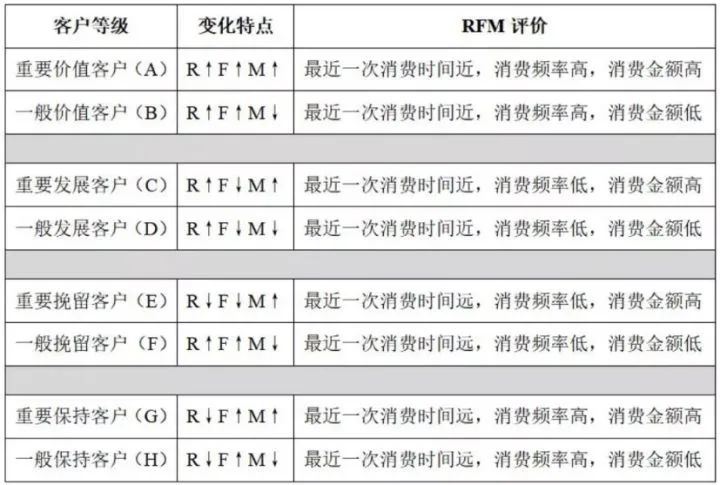
有了用户的细分,可以针对细分用户进行精细化的营销。比如针对【重要价值客户】应该做好用户的权益维系,针对【重要保持客户】做好客户的流失挽回。
关于模型的大体含义和应用价值,就简述一二,详细的请继续。
02
—
如何进行RFM建模
RFM模型的建立,总结起来一般可以分为以下几步。
(1)关于原始数据
从定义中我们可以看出来,R、F、M其实都是和消费相关的。因此,关于RFM模型的搭建,使用的原始数据很明确:订单表交易表。
而且,使用的维度其实并不需要很复杂,只要有以下的维度就足够了:
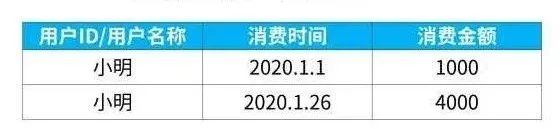
即我们只要有用户唯一标识、消费时间、消费金额,这三个字段的明细,就可以来搭建RFM的分析模型了。
当然,对于原始数据有一些数据清洗的工作,这里就不赘述了。比如选取的是成交的订单,而不是下单未支付的;比如选取的是排除大机构的订单……等等。
(2)三个维度的加工计算
基于上面的原始订单数据,下一步就是RFM三个维度的加工。这里面,有很多细节的问题。
首先,关于最近一次消费时间的计算。这个指标的定义比较明确,直接取最近一次消费的时间和当前时间做差就好。
关于消费频率的计算,必须有时间范围的设定。那具体是设置最近一年的消费频率(即购买了几次),还是最近1个月的消费频率呢?这是有很大差别的。通常来讲,这个范围的设定和分析用户的行业有很大关联。比如快消品,统计用户的几个月的时间就够了,但耐消品,显然不是。统计一年的,可能用户都没有复购。
关于消费金额。这里和消费频率一样,也是要有时间范围设定的,道理也是一样的。确定好了时间范围,直接做sum就行,没有太多的疑惑。
因此参数的设定,没有固定的标准,要多结合自己所处的行业规律。加工完是这样的表:

(3)阈值的划分
加工好了基础的三个维度的统计指标,接下来就是进行划分阈值的确定。即确定基于多大的数值,将每个维度的用户进行分段划分。
通常来讲,每个维度只需要确定一个阈值即可,这样可以将总体用户划分为8个分段。但现在还有一种套路是每个维度划分为5段,将总体划分为5^3共计125个分层,美其名曰【细分】。但我个人是不认可的。我觉得RFM分析的重要意义就是用户细分的可解释及可落地性,划分成125个用户群体,你该如何精细化运营呢?最终还是要进行合并。
OK,我们还是按照正常8分层来讲。我们看到上面的统计聚合表了,往往分布是下图的样子(以R为例):
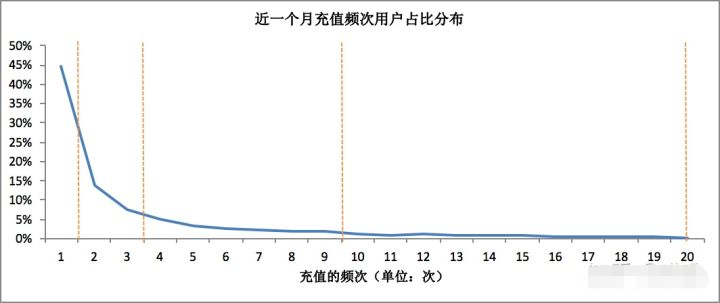
如何划分为两群用户呢?这时有很多种不同的方法了。
第一种方法,采取均值的方法。我个人是不太建议用均值作为阈值的。因为现实情况经常有一些异常值,会影响均值的计算。而数据清洗的时候很难都排掉异常。
第二种方法,是采取中位数(或者其他分位数,比如20%分位)的方法。这种方法直接将排序后的用户按照数量进行划分,中位数可以将人群一分为均等两份,其他分位数也可以有合理的业务解释:20%的用户贡献了80%的作用,等等。
这种方法个人觉得比较简单易行,比较推荐。
关于偏态分布(以右偏为例)下,众数、中位数、均值有以下关系:
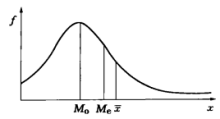
除了用统计量直接作为阈值外,第三种方法,也是市面上看到比较多的方法,就是打分法。
所谓的打分法,就是先将原始的R、F、M数值划分为1~5的分数,然后求分数均值,作为划分阈值。例如下图:

这种方法吧,挺忙活,又是打分又是求均值的。但我个人不太建议。一方面,原本只需要计算一个阈值就好了,现在需要先划分成5段,那这5段该怎么划分才合理呢?其次,这种打分的意义在哪,还增加了计算复杂度。
如果是解决异常值或者分布不均的问题,用分位数的方法就好了,我并没有太想明白市面上大行其道的打分法的意义在哪。我想到了一种可能,就是打分为了使三个维度可以在同一量纲上,进行衡量,以此可以计算一个用户的综合RFM得分,进行综合得分的排名。如下图:
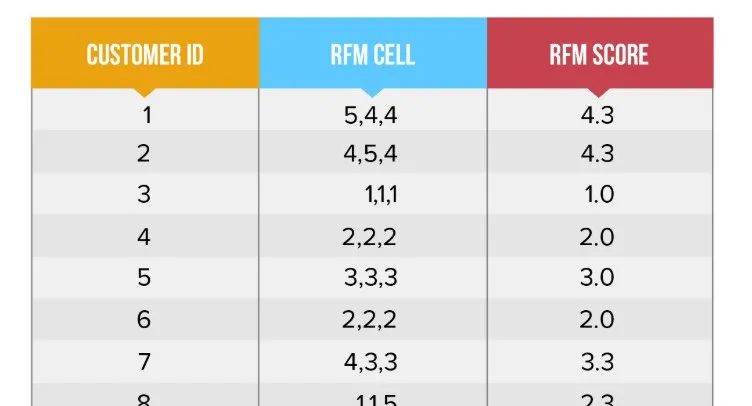
如果是这样,那我觉得,是不是用打分法就主要依赖于模型目标了。若为了划分为8个离散的用户层,就没必要打分;若为了求用户的综合RFM得分,需要打分。除此之外,我确实想不到打分的意义了。希望大神指点。
(4)用户分层计算
经历了上面不同阈值划分方法的纷争,下面就比较顺畅了,那就是用户分层的计算。
这一步比较容易理解,直接根据定好的三个阈值,判断每个用户属于哪个区间,然后打标即可。不赘述了。
(5)模型优化
所谓的模型优化,主要还是在于阈值的调整。
要随着最终划分的人群以及相关的运营效果、活动规律,调整阈值的设定,最终达到一个最合理的划分。
03
—
RFM模型的优缺点
本文开头也提到了,RFM模型的应用广泛,是有很大优点的,但缺点也是不少,现在来和大家一起探讨一下。
(1)模型的优点
最大的优点,应该是数据的可获得性。
目前在互联网中,基本对于数据的收集做的还是比较完备了,采集了用户的各种行为数据等,可以更好的进行用户打标签、分层的操作。但是在传统行业中,没有太多的行为数据,其实能用的数据比较有限。
但是,无论公司的数据做的有多不完备,也一定是有成交数据的(除非这个公司没收入……)。只要有成交数据,就能进行RFM的分析,这是最大的优势。而且,基于成交数据做的RFM模型,还是比较有效的。
其次,模型的分层可解释性强。
其他很多算法模型、机器学习模型,往往通过聚类进行用户的分层,对于业务来讲,不是很好解释。但RFM模型分成的8个用户类别,是非常好理解的。
(2)模型的缺点
RFM模型其实是滞后性的分析模型,只有当用户发生了购买行为后,才能进行RFM的分析。而且模型的前提假设就是用户的前后行为是无差别的。
另外,使用该模型需要注意的是,不同行业的应用,是有差别的。
最典型的是就是快消品和耐消品的差别。对于耐消品而言,RFM分析并不是一个很行之有效的模型。例如冰箱的购买,用户购买一台冰箱后可能十几年都没有购买了,这是没办法用RFM分析的。如果强搬硬套,是没有任何意义的。
以上。

●10个面试必会的统计学问题!
●品牌知名度分析