OPTICS

article/2025/9/30 15:06:12

OPTICS 就是一种基于密度的聚类算法，可以认为是dbscn的改进，改进之处主要是在不用每次调节eps和minpts都需要重新整个训练。其本质还是dbscan，只是能够在给定eps和minpts后，可以训练一次就可以在minpts值定对的情况下，尝试不同的eps’(eps’需要小于eps)来得到不同的结果。只不过由于算法需要，每个点得归属不是按照次序归为核心点，而是归为最近（如果距离小于核心距离的话就还是会受先后的影响）的核心点。

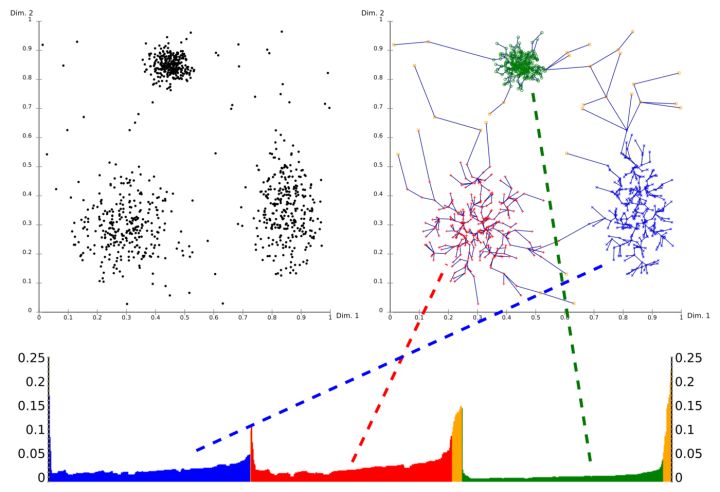
这种方法的思想就是当区域内点的密度大于某个阀值，就把这些点归于一类，因此这种基于密度的聚类算法天生就有很强的寻找离群噪音点的能力。一般来讲聚类算法最终得出的都是固定参数下的具体分类结果，而 OPTICS 则不然， OPTICS 最终得出的是一个在一定参数区间——最小领域半径（ε−neighborhood）下包含所有分类可能的点的序列，这个序列里的每个点都记录了它在此特定参数区间下的2个属性——核心距离（core distance）以及可达距离（reachability distance）。通过这个序列，我们可以很方便的得出在参数 ε' 下（当 ε' ≤ ε−neighborhood 时）数据点的分类结果。

综上所述，OPTICS具有2个很重要的特点：

1.抗离群噪音干扰的能力（寻找离群噪音点的能力）

2.对初始参数不敏感

OPTICS 需要的参数有2个，第一个就是前面提到的最小邻域半径（ε−neighborhood），这个参数的意义是对于每个点 P 而言，在半径为 ε 的范围内如果有其他点，那么这些点都算P的邻点，也就是说和P是在最小领域半径为 ε 的情况下是属于同一类的。

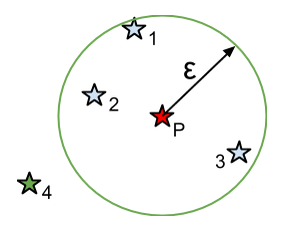
如上图所示，点1、2、3为点P在 ε 范围内的邻点，而点4则不是。所以点 P 有3个邻点，这样我们就会自然的想到 OPTICS 应该具有的第二个参数——最小邻点数（minimum number of points ： minpts）——对于点 P 而言，至少需要有多少个邻点才能证明自己是一个核心点（core point），也就是说自己是一个类别中最普通的一员，不是边界点，更不是一个离群的孤立点。 minpts 在这里也代表了密度聚类算法中的密度阀值，当 ε 范围内点的密度大于阀值 minpts，则说明 ε 范围内的点属于同一类别。

前面提到过，OPTICS 输出的序列中，每个点都有核心距离和可达距离两个属性。在最小领域半径为 ε ，最小邻点数为3的情况下（后面的例子中也默认为这样），如上图所示，点 P 具有4个邻点，而到点1的距离是点 P 刚好满足至少有3个邻点的半径，所以取点 P 到点1的距离为点 P 的核心距离。对于点4和点1而言，它们的可达距离就是其到点 P 的距离。而对于点2和点3而言，由于它们到点 P 的距离小于点 P 的核心距离，因此，设置它们的可达距离等于点 P 的核心距离。

也就是说对于每个点 P 而言，假设让其刚好满足最小邻点数的点为 P' ，则P的核心距离等于其到点 P' 的距离，其他情况为正无穷。

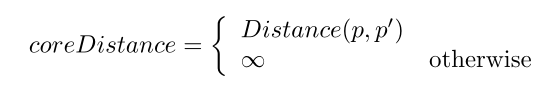
对于核心点 P 的邻点 P1、P2、…Pn 而言，如果其到点 P 的距离大于点 P 的核心距离，则其可达距离为该点到点 P 的距离，如果小于等于点 P 的核心距离，则其可达距离等于点 P 的核心距离。

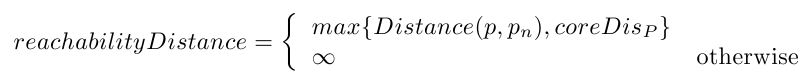
OPTICS的具体步骤是：

1: procedure runOPTICS(X, ε, minpts)

2: while point x ∈ X unprocessed and unchecked do

3: dis ← distance(x, X)

4: if x is corePoint then

5: mark x as processed

6: N ← getNeighbors(x, ε, dis)

7: setCoreDistance(x, N, ε, minpts)

8: O ← x; Q ← N

9: update(x, N, Q)

10: while Q ≠ empty do

11: y ← extractMinRD(Q)

12: mark y asprocessed

13: O ← y

14: dis ← distance(y, X)

15: if y is corePoint then

16: N' ← getNeighbors(y, ε, dis)

17: setCoreDistance(y, N', ε, minpts)

18: Q ← N'

19: update(y, N', Q)

其中 X 是原始的点的数据集合，O 作为最后输出结果的点集的有序序列，Q 是一个无重复元素的队列，保存了当前已找到但是还没处理过的属于同一类别的点的集合。算法首先遍历输入的点集 X ，找到一个核心点，如果找不到，则直接结束算法，如果找到一个点 x 为核心点，则设置 x 的核心距离以及可达距离并将其加入输出序列 O，将其所有邻点加入队列 Q。之后从队列 Q 中找出可达距离最小的点 y，将其加入输出序列，如果 y 也是核心点，则将 y 的所有邻点加入到并且更新队列 Q。重复以上步骤直到处理完所有的点。其中的 update 函数的功能是更新队列 Q 中点的可达距离。