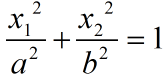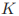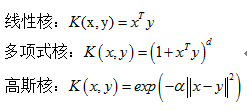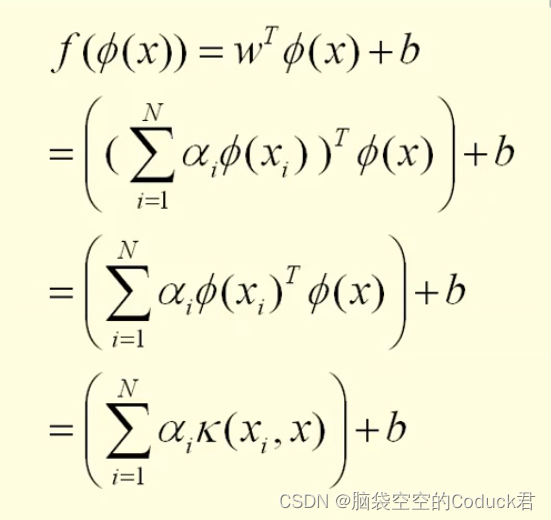机器学习中的核函数与核方法（是什么？为什么？怎么做？）

article/2025/9/25 15:49:43

我们在学习机器学习的时候，总是会看到一个概念——核，然后看到一堆公式。但是为什么要核呢？核到底是啥玩意？云里雾里。接下来，我们将要把“核”这个东西的神秘面纱一点点揭开。

一、什么是“核函数”

我们都知道，机器学习（神经网络）的一个很重要的目的，就是将数据分类。我们想象下面这个数据（图1），在二维空间（特征表示为 $\small x_1$ 和 $\small x_2$ ）中随机分布的两类数据（用圆圈和叉叉表示）。

如果我们想要将这两类数据进行分类，那么分类的边界将会是一个椭圆:

$\small \frac{x_1^2}{a_1}+\frac{x_2^2}{a_2}=1$

但是如果我们可以通过一个映射，将数据的特征 $\small (x_1,x_2)$ 通过某个非线性映射 $\small \phi$ 映射到三维空间，其特征表示为 $\small (z_1,z_2,z_3)$ ，并且映射关系为 $\small (z_1,z_2,z_3)==\phi (x_1,x_2)=(x_1^2,2^{1/2}x_1y_1,x_2^2))$ ,那么我们是不是就可以用一个平面来将其分类，也即是将上述椭圆的x特征换成z特征：

$\small \frac{z_1}{a_1}+0\cdot z_2+\frac{z_3}{a_2}=1$

其实这个映射，就是将一个空间中的特征转换到另外一个空间，这就是空间转换（映射）的意义，即可以将原来线性不好分的数据转换到另外一个空间，在这个空间中可以用一个超平面线性可分。

在机器学习中，我们要用到内积运算。而在映射后的高维空间中，内积往往是很不好求解的。所以，我们能不能找到在低维空间中的某个运算，恰好等于高维空间中的内积运算呢？

设在原空间中有两个点 $\small (x_1,x_2)$ 和 $\small (x_1^{'},x_2^{'})$ ，映射到高维空间中变成 $\small (z_1,z_2,z_3)$ 和 $\small (z_1^{'},z_2^{'},z_3^{'})$ ，我们来看这个例子中的高维空间的内积运算：

$\small <(z_1,z_2,z_3),(z_1^{'},z_2^{'},z_3^{'})> =<(x_1^2,2^{1/2}x_1x_2,x_2^2),(x_1^{'}^2,2^{1/2}x_1^{'}x_2^{'},x_2^{'}^2)> =(<x,x^{'}>)^2$

我们就将低维空间中的这个对于内积的运算定义为核函数 $\small \kappa (x,x^{'})=(<x,x^{'}>)^2$ 。换句话说，核函数就是低维空间中的内积的某个函数，或者写成 $\small \kappa (x,x^{'})=g(<x,x^{'}>)$ ，因为在别的例子中，有可能不是内积的平方。即核函数就等于就是高维空间的内积。

二、为什么要用核函数

因为在机器学习中，我们求解的过程要用到内积，而变换后的高维空间的内积我们不好求，所以我们定义了这个核函数，可以把高维空间的内积运算转化成内为空间的某些运算，这样求起来不是很简单吗？

换句话说，如果我们有了核函数，我们就不再需要知道那个映射 $\small \phi$ 到底是个什么鬼，我们就可以直接通过核函数，就可以求导高维空间的内积了，从而可以计算出高维空间中两个数据点之间的距离和角度。

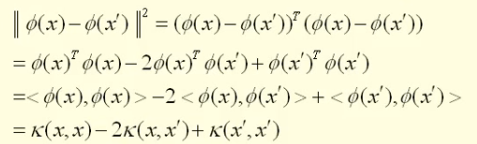
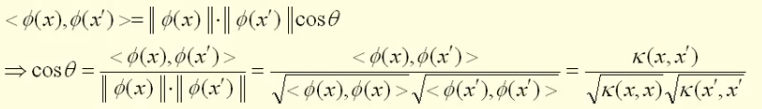
三、怎么用？（一个简单的分类例子）

现在我们假设，有N个数据{ $\small {(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}$ }，其中 $\small x_i=(x_{i1},x_{i2},...,x_{ip})$ 是第i个数据的p维特征， $\small y_i$ 是第i个数据的分类标签,现将其映射到高维空间变成 $\small [{(\phi(x_1),y_1),(\phi(x_2),y_2),...,(\phi(x_N),y_N)]$ ，而在这个空间中，有两个类别，所以标签可以假定为+和-，其中每一类的样本个数为 $\small n_+$ 和 $\small n_-$ 。正样本的中心点 $\small C_+=\frac{1}{n_+}\sum_{y_i=+}\phi( x_i)$ ，负样本的中心点 $\small C_-=\frac{1}{n_-}\sum_{y_i=-} \phi(x_i)$ ，从 $\small C_-$ 到 $\small C_+$ 有一条差向量 $\small w=C_+-C_-$ ，而w的中心点为C，所以在C点垂直于w的超平面就是两类的分类边界。

而想要把某个数据 $\small \phi(x)$ 分类为+的依据为：从C点到样本点的向量差与w向量的夹角应该小于90°，也即: $\small 0<cos\theta<1$ ；反之， $\small \small 0>cos\theta>-1$ 。即，当内积为正，那就说明在分类1，内积为负，就说明在分类2。即：

$\small y=sgn(<\phi(x)-C,w>)=sgn(w^{T}\phi(x)-w^{T}C)$

于是我们来 $\small cos\theta$ 的表达式：

$\small cos\theta=\frac{<\phi(x)-C,w>}{|\phi(x)-C||w|} =\frac{1}{a}<\phi(x)-C,w>= \frac{1}{a}(<\phi(x),w>-<C,w>)$

(PS:说到这，你应该知道为什么分类需要内积了吧？因为内积的正负代表了数据点是位于分类边界的正方向还是负方向，从而实现分类。)

其中:

$\small w=C_+-C_-=\frac{1}{n_+}\sum_{y_i=+}\phi( x_i) -\frac{1}{n_-}\sum_{y_i=-}\phi( x_i)$

$\small C=\frac{1}{2}(C_++C_-)=\frac{1}{2}(\frac{1}{n_+}\sum_{y_i=+}\phi( x_i) -\frac{1}{n_-}\sum_{y_i=-}\phi( x_i))$

$\small <\phi(x),w>=<\phi(x),\tfrac{1}{n_{+}} \sum_{y_{i}\in +}\phi(x_{i})- \tfrac{1}{n_{-}} \sum_{y_{i}\in -}\phi(x_{i})> =\tfrac{1}{n_{+}} \sum_{y_{i}\in +}<\phi(x),\phi(x_{i})>+ \tfrac{1}{n_{-}}\sum_{y_{i}\in -}<\phi(x),\phi(x_{i})> =\tfrac{1}{n_{+}} \sum_{y_{i}\in +}\kappa (x,x_{i})+ \tfrac{1}{n_{-}}\sum_{y_{i}\in -}\kappa (x,x_{i})$

$\small <C,w>=$

后面的就不继续写了，化简形式都一样，即：我们就可以把高维空间的内积，改写成低维空间的核函数的形式，这样在不知道映射 $\small \phi$ 是个什么鬼的情况下吗，也可以轻松地进行分类工作了。

四、补充一点

1. 有限半正半定：给定任意有限 n个点（x1~xn）,求解其矩阵是正定的：

$\small \kappa =\begin{bmatrix} \kappa(x_1,x_1) & ... &\kappa(x_1.x_n) \\ ...& ... & ...\\ \kappa(x_n,x_1)&... & \kappa(x_n,x_n) \end{bmatrix} \geq 0$