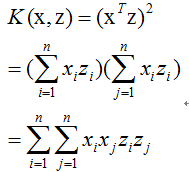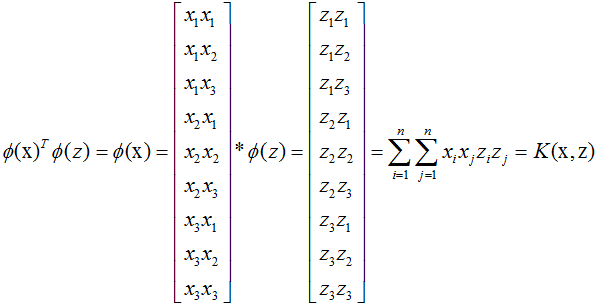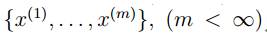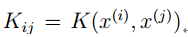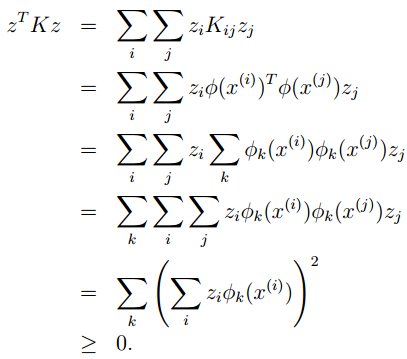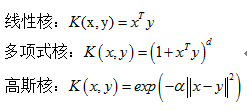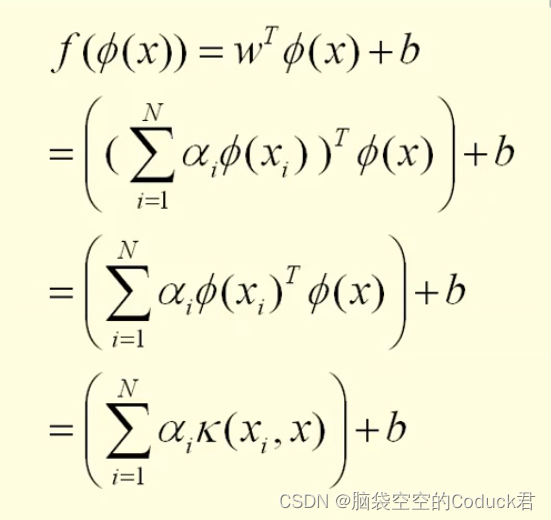核方法原理

1.无力的线性分类器

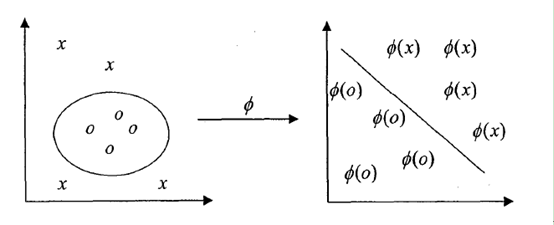
一般情况下，我们考虑构造一个线性分类器来解决问题。但是实际中，线性分类器的效果达不到要求，因为大部分数据都不是线性可分的，如下面这幅图。一种改进的方法是把多个弱的线性分类器组合得到一个强分类器，如决策树，booting方法；另一个种方法就是接下来要说的高维投影。

2.高维线性可分

如果某个分类问题线性不可分，那么我们可以考虑把样本投影到非线性的高维空间上，从而实现高维可分。R（低维）->F（高维）。如下图。

3.高维计算的维数灾难

上面的映射会大大增加计算复杂度，因为投影需要计算复杂度，维数增加后再分类也要增加计算复杂度。

4.巧妙的核技巧（kernel trick）

有人发现了一些函数的特性，设为K（x,y）。有人发现，K（x,y）=<φ(x)* φ(y)>，也就是低维的函数（K（x,y）），可以得到高维空间的内积（<φ(x)* φ(y)>）。而如果内积<φ(x)* φ(y)>是我们投影到高维后，构造分类器所需要的主要计算，显然，我们只要在低维空间计算K（x,y）。通常情况下，K的计算复杂度会大大小于高维内积<φ(x)* φ(y)>。

以简单的线性核函数为例子阐述如下：

 

而考虑高维点积如下：

即核函数结果等于高维内积。

在考虑其时间复杂度：

核函数第一步的计算为N为向量点积后得到实数相乘，复杂度为O（N）。

高维投影后，两个N^2的向量点积，时间复杂度为O（N^2）。

 

也就是说，我们通过核函数，用低维的计算量得到了高维的结果，没有增加计算复杂度的同时，得到了性质更好的高维投影。也就是kernel trick。

5.广泛存在的内积运算

通过上面我们可以看出，只要涉及到内积运算，我们都能够运用核函数替代来得到高维投影的内积。而内积广泛存在于各种算法当中，最典型的有SVM，KNN,线性回归，聚类等。一些使用最小平方误差作为目标函数的方法也可以扩展为核最小平方误差。

6.常见的核函数

Mercer定理

那么，怎样的函数，得到的结果会是原向量的高维内积呢？如下推导核函数的Mercer定理。

对于给定的任意向量集合：

核矩阵定义为任意两个向量核函数组成的矩阵，也就是：

对于任意的矩阵z，根据内积的非负性，我们有：

也就是说，K如果是核函数，那么对于任意的样本集合，得到的核矩阵为半正定矩阵。

被证明可用的常见核函数如下

 

总结

核方法的好处

1.      在线性与非线性间架起一座桥梁

2.      通过巧妙地引进，避免了维数灾难，没有增加计算复杂度。