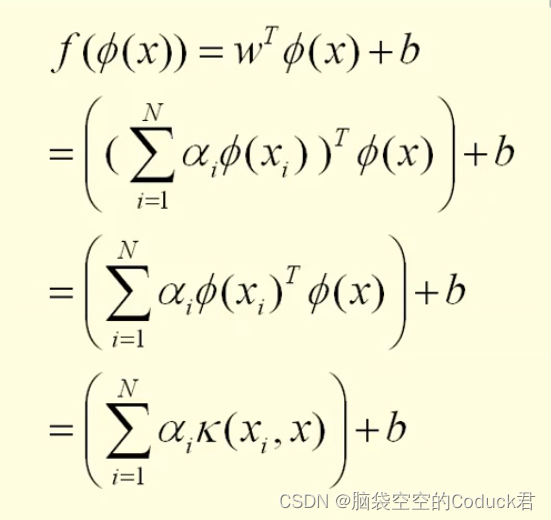前一篇主要梳理了几个基本概念以及相关关系,这一篇主要针对核方法的应用进行讨论,并理解核方法的思想,了解为什么要引入核方法。
核方法在机器学习中是一种灵活的技术,主要归结为两个方面:
- 非线性问题转换为高维线性问题;
- 只依赖于内积的问题。
具体来说,核方法可扩展支持向量机(SVM)、主成分分析(PCA)等算法,用于处理数据在低维空间不是线性可分的,通过核变换在高维空间就可以变成线性可分得以求解的问题,这样就有了非线性决策边界的核支持向量机(Kernel SVM)以及可以对非线性数据降维的核主成分分析(KPCA);此外,还可以用于扩展其他只依赖于样本点之间的内积的算法,例如核岭回归(Kernel ridge regression,KRR)等。下面利用最简单的二分类问题来理解核方法的理念。
例如下图从左到右分别对应了线性可分的情况、允许存在少量异常点进行线性可分的情况以及线性不可分的情况:

对于线性可分的问题(即存在一个超平面可以将不同类别的样本完全划分开),我们可以采用感知机(Perception)或者硬间隔支持向量机(Hard-margin SVM)。但如果存在少量异常点,可以采用口袋算法(Pocket Algorithm)或者软间隔分类器(Soft-margin SVM),但是图三这种明显是不能线性可分的,不能找到一条直线将样本很好的划分,为解决非线性可分问题,主要有一下两种方法:
- 从感知机出发,增加隐层数量,由万能逼近定理(Universal approximation theorem)可以用神经网络来逼近任意的连续函数,得到非线性的决策边界。
- 通过核方法,进行非线性变换,将非线性可分的问题转化为线性可分的问题。
因此,利用kernel就上述处理方法可以归结为:
| 线性可分问题 | 允许存在少量异常点 | 严格线性不可分 |
|---|---|---|
| 感知机学习算法(PLA) | 口袋算法(Pocket Algorithm) | kernel+PLA |
| Hard-margin SVM | Soft-margin SVM | kernel+Hard-margin SVM(Kernel SVM) |
非线性问题转换为高维线性问题
用最简单的异或问题来阐述

上述问题是线性不可分的,做如下变换:
x = ( x 1 , x 2 ) ⇓ z = ( x 1 , x 2 , ( x 1 − x 2 ) 2 ) \begin{aligned} x&=(x_1,x_2)\\ &\Downarrow\\ z&=(x_1,x_2,(x_1-x_2)^2) \end{aligned} xz=(x1,x2)⇓=(x1,x2,(x1−x2)2)

将二维的线性不可分问题通过核变换转化为三维中线性可分的问题,上图中任意一个(0,1)之间的灰色平面都可以将上述异或问题线性划分,由Cover定理可知,高维空间比低维空间更易线性可分。
Cover定理:将复杂的模式分类问题非线性地投射到高维空间将比投射到低维空间更可能是线性可分的。(来自百度百科)
只依赖于内积的问题
对于Hard-margin SVM,它的基本模型可写为:
min ω , b 1 2 ∥ ω ∥ 2 s . t . y i ( ω T x i + b ) ⩾ 1 , i = 1 , 2 , … , m . \begin{aligned} &\min_{\omega,b}{1\over2}\|\omega\|^2\\ &s.t.\ y_i(\omega^Tx_i+b)\geqslant1,\ i=1,2,\dots,m. \end{aligned} ω,bmin21∥ω∥2s.t. yi(ωTxi+b)⩾1, i=1,2,…,m.
它的对偶问题可以写为:
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j x i T x j s . t . ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , … , m . \begin{aligned} &\max_{\alpha}\sum_{i=1}^m\alpha_i-{1\over2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jx_i^Tx_j\\ &s.t.\ \sum_{i=1}^m\alpha_iy_i=0,\ \alpha_i\geqslant0,\ i=1,2,\dots,m. \end{aligned} αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjxiTxjs.t. i=1∑mαiyi=0, αi⩾0, i=1,2,…,m.
正如上述讨论的那样,Hard-margin SVM是针对线性可分的问题求解,如果对于线性不可分的,还需要做一个非线性变换,将 x → ϕ ( x ) x\to\phi(x) x→ϕ(x),即将 x x x映射到它的特征空间,这样的话上述对偶问题中就变为 x i T x j x_i^Tx_j xiTxj之间的内积就变为计算 ϕ ( x i ) T ϕ ( x j ) \phi(x_i)^T\phi(x_j) ϕ(xi)Tϕ(xj)。
由于特征空间维数可能很高,甚至可能是无穷维的,因此直接计算 ϕ ( x i ) T ϕ ( x j ) \phi(x_i)^T\phi(x_j) ϕ(xi)Tϕ(xj)通常是很困难的,为了避免直接计算高维空间中的内积,我们引入核函数
k ( x i , x j ) = ⟨ ϕ ( x i ) , ϕ ( x j ) ⟩ = ϕ ( x i ) T ϕ ( x j ) k(x_i,x_j)=\langle \phi(x_i),\phi(x_j)\rangle=\phi(x_i)^T\phi(x_j) k(xi,xj)=⟨ϕ(xi),ϕ(xj)⟩=ϕ(xi)Tϕ(xj)这样,它的对偶问题就可表示为
max α ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j k ( x i , x j ) s . t . ∑ i = 1 m α i y i = 0 , α i ⩾ 0 , i = 1 , 2 , … , m . \begin{aligned} &\max_{\alpha}\sum_{i=1}^m\alpha_i-{1\over2}\sum_{i=1}^m\sum_{j=1}^m\alpha_i\alpha_jy_iy_jk(x_i,x_j)\\ &s.t.\ \sum_{i=1}^m\alpha_iy_i=0,\ \alpha_i\geqslant0,\ i=1,2,\dots,m. \end{aligned} αmaxi=1∑mαi−21i=1∑mj=1∑mαiαjyiyjk(xi,xj)s.t. i=1∑mαiyi=0, αi⩾0, i=1,2,…,m.再和求解线性可分的SVM方法一样,利用拉格朗日乘数法,求导为零,得到分割超平面方程为:
f ( x ) = ω T ϕ ( x ) + b = ∑ i = 1 m α i y i ϕ ( x i ) T ϕ ( x ) + b = ∑ i = 1 m α i y i k ( x , x i ) + b \begin{aligned} f(x)&=\omega^T\phi(x)+b\\ &={\sum_{i=1}^m} \alpha_iy_i\phi(x_i)^T\phi(x)+b\\ &={\sum_{i=1}^m} \alpha_iy_ik(x,x_i)+b \end{aligned} f(x)=ωTϕ(x)+b=i=1∑mαiyiϕ(xi)Tϕ(x)+b=i=1∑mαiyik(x,xi)+b这里的 k ( ⋅ , ⋅ ) k(\cdot,\cdot) k(⋅,⋅)就是核函数。上式表明,分割超平面就是核函数的一些线性组合,即模型的最优解可以通过训练样本的核函数来得到。
总结
- 正如前面一篇博客中讨论的那样,任何一个核函数都是再生核函数,对应都隐式的定义了一个RKHS,这个RKHS也是这个核函数的特征空间,但是是一个特殊的特征空间,因为具有再生性 k ( x , x ′ ) = < k ( ⋅ , x ) , k ( ⋅ , x ′ ) > k(x,x') = <k(\cdot, x), k(\cdot,x')> k(x,x′)=<k(⋅,x),k(⋅,x′)>;核函数的特征空间不唯一,甚至可以不是函数空间,而是其它类型的希尔伯特空间。
- 一般说来特征空间是很高维的,也就是说,在核函数给定的情况下,可以把低维的输入空间通过一个非线性变换对应于一个特征空间,在这个高维空间中利用解线性可分问题的方法来求解非线性可分问题,这种学习是隐式地在特征空间中进行的,不需要显式地定义特征空间和映射函数,这样的方法就称为核方法(Kernel Method)
- 我们所需要做的就是找到一个好的非线性变换,即选取一个好的核函数甚至会手动设计一个好的特征映射(例如计算机视觉方面)。
- 在实际使用时不用管特征空间或者RKHS,但是如果想要做先验分析,也就是回答什么样的问题适合这个方法,则需要讨论RKHS。
参考资料:
机器学习,周志华
统计学习方法,李航
Foundations of Machine Learning,Mehryar Mohri
参考视频:白板推导系列(七)-核方法(Kernel Method)