核方法概述----正定核以及核技巧（Gram矩阵推导正定核）

article/2025/9/25 18:50:23

在再谈SVM（hard-margin和soft-margin详细推导、KKT条件、核技巧）中我们大致谈到了核函数以及为什么要用核函数，今天在这里更加详细的介绍一下。

核方法

1.核函数概述
2.正定核
- 2.1定义
- 2.2证明
3.核技巧
4.常见的核函数

1.核函数概述

从前面的学习中我们可以看出来，无论是Hard margin SVM还是Soft margin SVM构建的都是一个线性的决策边界，从而把数据集分到各自的类中，如果数据集是一个非线性的，直接使用SVM，得不到一个理想的结果，那么使用线性分类器求解非线性分类问题，需要特殊的处理：

首先，使用一个变换将原空间的数据映射到新空间中
然后，在新空间中使用线性分类器求解

在机器学习之逻辑回归(logistics regression)中，我们考虑了这样一个问题：
在这里插入图片描述
考虑一个简单的二分类问题，有x1,x2两个特征，两个特征值都为0 or 1为C2，否则为C1。在逻辑回归中，输入某一个样本的两个特征值x1，x2，与各自的权重w1,w2相乘，也就是求inner product，最后加上一个bias，得到z，再将z用Sigmoid函数处理，最后与0.5进行比较，就可以判断属于哪一个类别。但是我们将两个特征映射到到一个二维坐标系上，发现根本不可能找到一条直线将两类样本完全分开。这种限制与数据量无关，是逻辑回归自己本身的限制。
鉴于上面这种情况，就需要用到Teature Transformation，即特征转换。用特征转换处理后，使得我们能够用一条直线将C1和C2，也就是上面的红点和蓝点分开。图里面的处理方法是：定义新的x1,x2，x1为点到(0,0)的距离，x2为到点(1,1)的距离，处理后如下图所示：
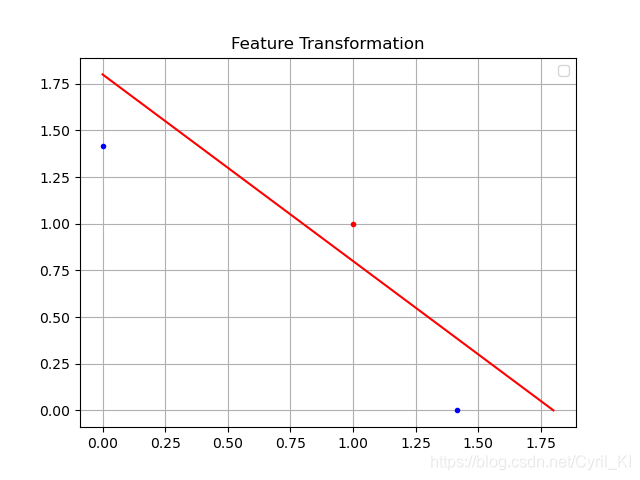
在这里插入图片描述
这时候我们发现，就能够找到一条直线将两类点分开，但在实际应用中，我们往往不能够找到比较好的特征变换的方法。
上面这种其实还是只是二维到二维的转换，实际上我们可以是二维到三维的转换，比如下面这种情况：
在这里插入图片描述
同样形状与颜色的点代表同一类别。观察上图我们发现，在二维平面上，我们不可能找到一条直线恰好可以将两类样本点分开，但假设我们做如下处理：

这样我们就将二维的点变换到了三维，这个时候我们再看看分布情况：
在这里插入图片描述

这个时候两个蓝点在一个平面上，两个红点在另一个平面上，在它们之间很容易找到一个超平面来使得它们分开。

上面啰嗦了一大堆，总结一下就是：当我们在低维空间对样本数据处理时，我们发现用线性的模型无法处理。于是我们便把低维数据引入到高维中，这样就可以用线性的模型去处理。

2.正定核

我们所说的核函数大部分都是正定核。在下面的探讨中，输入空间为 $\chi$ ， $x,z\in\chi$ 。

2.1定义

正定核的定义有两种：

对于 $\forall x,z\in\chi$ ，若存在一个函数 $\phi$ ，使得 $K(x,z)=\ <\phi(x),\phi(z)>$ ，则称 $K (x, z)$ 为正定核函数
对于 $\forall x,z\in\chi$ ，如果 $K (x, z)$ 满足对称性以及正定性，则我们也称 $K (x, z)$ 为正定核函数

对第一条定义的说明：我们要将低维样本映射到高维，则我们需要一个映射函数，如果我们能够找到一个 $\phi$ 函数，使得我们定义的 $K (x, z)$ 恰好是两个高维样本 $\phi(x),\phi(z)$ 的内积，则 $K (x, z)$ 就是一个正定核函数。但上面我们也说了，这个映射函数很不好找。
为啥一定要是内积？因为内积恰恰是数据挖掘中非常重要的一种计算方式，数据挖掘的很多方法都是借助内积来完成的，所以核函数具有强大的功能。
对第二条定义的说明：

所谓对称性，是指 $K (x, y) = K (y, x)$ 。
所谓正定性：对低维空间中任意N个样本 $x_{1},x_{x},...,x_{N}$ ，其对应的Gram矩阵是半正定的。什么是Gram矩阵？我们令K表示那N个样本的Gram矩阵：

该矩阵是一个N X N的矩阵，比如（1，1）这个位置就是 $K(x_{1},x_{1})$
什么是半正定？我们任取一个N维的列向量 $\alpha$ ，如果满足：

则说明这个N X N的矩阵K是一个半正定的矩阵。

2.2证明

我们一再强调，映射函数 $\phi$ 不好找。 那么我们该怎么定义一个正定核？瞎猜吗？显然不是，我们可以根据第二个定义来构造。因此我们需要证明一二两个定义式互通的。
将一二两个定义结合起来就是：
$K(x,z)=<\phi(x),\phi(z)>$ $\Leftrightarrow$ Gram矩阵半正定且K满足对称性。
下面我们将证明这个结论。先看从左到右，假设已知了 $K(x,z)=<\phi(x),\phi(z)>$ ，因为是求内积，所以对称性是显而易见的。那么我们怎么推导出Gram矩阵半正定呢？根据半正定的定义：
在这里插入图片描述
因此正推可以实现。反推暂时不太会。。后期补上。
因此上述两个定义是相通的。在定义一中，我们得找到一个 $\phi$ ，这个通常不好找。而在定义二中，我们只需要自己定义一个函数K，然后取任意N个样本，联合K求它们的Gram矩阵，只要该矩阵满足半正定性质，那么我们定义的函数K就是一个正定核函数。

3.核技巧

什么是核技巧？在SVM的推导中，我们看到：
在这里插入图片描述

注：上述 $x_{j}$ 只是为了便于区分才这样写，实际上是 $x_{i}$ 。我们令：
在这里插入图片描述
于是有：

所谓核技巧，就是指我们可以直接计算 $K(x_{i},x_{j})$ （这个K是已知的，根据定义二可以构造），而不需要真正的去找一个 $\phi(x)$ （通常是很难找的）。也就是说，我们并不关心低维到高维的映射 $\phi$ 是什么样子的，我们只需要构造一个函数K，使得该函数可以表示为映射后空间里数据的内积，这样就可以了。