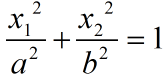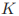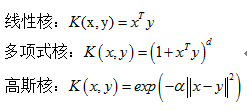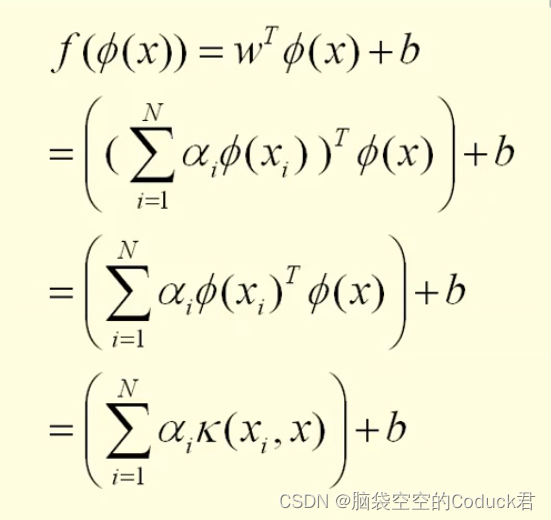本文对核方法（kernel method）进行简要的介绍。

核方法的主要思想是基于这样一个假设：“在低维空间中不能线性分割的点集，通过转化为高维空间中的点集时，很有可能变为线性可分的” ，例如下图

 

 

左图的两类数据要想在一维空间上线性分开是不可能的，然而通过F(x)=(x-a)(x-b)把一维空间上的点转化为右图上的二维空间上，就是可以线性分割的了。

然而，如果直接把低维度的数据转化到高维度的空间中，然后再去寻找线性分割平面，会遇到两个大问题，一是由于是在高维度空间中计算，导致curse of dimension问题；二是非常的麻烦，每一个点都必须先转换到高维度空间，然后求取分割平面的参数等等；怎么解决这些问题？答案是通过核戏法（kernel trick）。

（pku, shinningmonster, sewm)

Kernel Trick: 定义一个核函数K(x1,x2) = <\phi(x1), \phi(x2)>, 其中x1和x2是低维度空间中点（在这里可以是标量，也可以是向量），\phi(xi)是低维度空间的点xi转化为高维度空间中的点的表示，< , > 表示向量的内积。

这里核函数K(x1,x2)的表达方式一般都不会显式地写为内积的形式，即我们不关心高维度空间的形式。核函数巧妙地解决了上述的问题，在高维度中向量的内积通过低维度的点的核函数就可以计算了。这种技巧被称为Kernel trick。这里还有一个问题：“为什么我们要关心向量的内积？”，一般地，我们可以把分类（或者回归）的问题分为两类：参数学习的形式和基于实例的学习形式。

参数学习的形式就是通过一堆训练数据，把相应模型的参数给学习出来，然后训练数据就没有用了，对于新的数据，用学习出来的参数即可以得到相应的结论；

而基于实例的学习（又叫基于内存的学习）则是在预测的时候也会使用训练数据，如KNN算法。而基于实例的学习一般就需要判定两个点之间的相似程度，一般就通过向量的内积来表达。从这里可以看出，核方法不是万能的，它一般只针对基于实例的学习。

紧接着，我们还需要解决一个问题，即核函数的存在性判断和如何构造？ 既然我们不关心高维度空间的表达形式，那么怎么才能判断一个函数是否是核函数呢？

Mercer 定理：任何半正定的函数都可以作为核函数。所谓半正定的函数f(xi,xj)，是指拥有训练数据集合（x1,x2,...xn)，我们定义一个矩阵的元素aij = f(xi,xj)，这个矩阵式n*n的，如果这个矩阵是半正定的，那么f(xi,xj)就称为半正定的函数。这个mercer定理不是核函数必要条件，只是一个充分条件，即还有不满足mercer定理的函数也可以是核函数。常见的核函数有高斯核，多项式核等等，在这些常见核的基础上，通过核函数的性质（如对称性等）可以进一步构造出新的核函数。SVM是目前核方法应用的经典模型。

上述是目前我所理解到的核方法的主要精神。