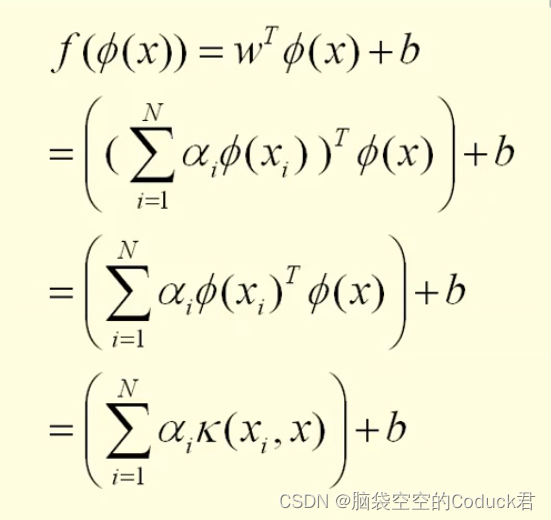核方法(kernel method)的主要思想

article/2025/9/25 18:40:16

kernel method是针对低维线性不可分而提出的一种解决方法，在PRML中有一章节的介绍，对其理解，也是迭代更进的过程。

简单来说，kernel method是一种低维和高维特征空间映射的方法，利用低维内积的函数来表征高维内积，即高维的内积用低维内积的函数来表示，这个低维内积的函数就是kernel function。

首先，说明kernel method的示例
说到机器学习中的核方法（Kernel Method），大部分人应该是在学习SVM的时候认识到它或者听说它。它的基本思想是说，普通的SVM分类超平面只能应对线性可分的情况，而对于线性不可分的情况我们则需要引入一个Kernel，这个Kernel可以把数据集从低维映射到高维，使得原来线性不可分的数据集变得线性可分。

(关于在SVM中应用Kernel Trick的具体方法及示例，有兴趣的读者可以参考文献【1】《R语言实战：机器学习与数据分析》以了解更多。)

一、基本概念

本节我们将抛开SVM，直面Kernel Method的本质。首先来看一个简单的例子，下面的左图中有些数据集，在原来的二维平面上它们是线性不可分的。如果要对它们进行分类，则需要用到一个椭圆曲线：

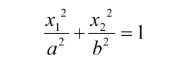
然后为了设计了一个feature mapping，将原来的二维特征空间转换到新的三维特征空间中，具体来说我们所使用的mapping函数Φ如下：

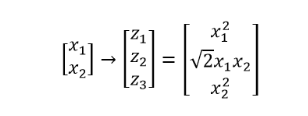
基于上面这种映射，我们就会得到下图右侧所示的新的三维特征空间，而在这个新的特征空间中，只要用一个分割超平面就可将原来的两组数据分开，换言之，原来线性不可分的数据现在已经变得线性可分了！这就是Kernel的很重要的作用。

之前给定的基于映射，你其实就可以写出新的分割超平面的方程如下：

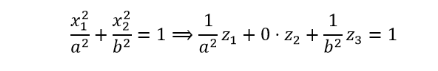
在一个Hilbert空间中，最重要的运算就是“内积”，下面我们要做的事情就是看看如何利用已知的原空间中的信息来计算新空间中的内积。例如，现在有两个点：

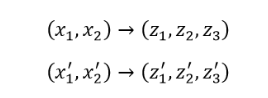
如下图所示，我们发现新空间中任意两个点的内积，可以通过一个关于原空间中之内积的函数来得到，我们就定义这样的一个函数为核函数（Kernel Function）。

而内积又可以作为一种相似性的度量（例如如果两个向量彼此正交，那么它们的内积就为零），因此我们可以定义Kernel Function为：is a similarity measure that can be written as

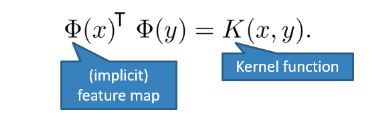
更重要的是上面的算例告诉我们，似乎我们并不需要知道feature mapping Φ 到底长什么样子，而是只要知道K，就可以通过原空间中两个点的内积算得新空间中对应的两个点之间的内积。

再举一个例子。对于一个Polynomial kernel，注意其中的x和y是两个向量，

我们便可以计算新空间中x和y对应的两个点的内积为

而且它同样具有“使得原本线性不可分的数据集在新空间中线性可分”的能力（注意我们仅仅使用了新空间中的两个维度）。

引用文献【2】中的话做一个小结“Kernel method work by embedding data in a vector space (usually with more high dimensionality) to look for (linear) relations in such space. if map is chosen suitably, complex relations can be simplified and easily detected”。

下表列出了常用的Kernel Function，值得注意的是RBF Kernel（又称高斯核）是一个典型的会将原空间投影到无穷维空间的核函数。关于这些核的具体讨论，以及为什么高斯核是无穷维的，都可以参考文献【3】以了解更多细节。

二、核矩阵

相信读者对于内积矩阵（又称Gram矩阵）并不陌生，如果你对这个概念不甚了解，可以参考文献【4】中3.2.6小节“希尔伯特空间”（第118页）中的相关内容。特别地，该小结中还证明了“Gram矩阵”是半正定（PSD）对称矩阵这一结论。

A real symmetric m×m matrix K satisfying

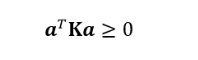
In addition, we have

A real symmetric matrix is diagonalizable.
A real symmetric matrix is PSD if and only if all its eigenvalues are non-negative.

假设我们的数据集中有N个点，那么我们可以定义一个核矩阵（其实就是Gram矩阵），该矩阵中存放的就是这N个点在新空间中对应的N个点彼此之间的内积。

三、默瑟定理

紧接着，我们还需要解决一个问题，即核函数的存在性判断和如何构造？既然我们不关心高维度空间的表达形式，那么怎么才能判断一个函数是否是核函数呢？

Mercer 定理：任何半正定的函数都可以作为核函数。所谓半正定的函数f(xi,xj)，是指拥有训练数据集合（x1,x2,...xn)，我们定义一个矩阵的元素aij = f(xi,xj)，这个矩阵式n*n的，如果这个矩阵是半正定的，那么f(xi,xj)就称为半正定的函数。这个mercer定理不是核函数必要条件，只是一个充分条件，即还有不满足mercer定理的函数也可以是核函数。常见的核函数有高斯核，多项式核等等，在这些常见核的基础上，通过核函数的性质（如对称性等）可以进一步构造出新的核函数。SVM是目前核方法应用的经典模型。

前面我们谈到，似乎feature mapping Φ 到底长什么样子并不那么重要，只要我们有K就可以了。于是我们有如下两个疑问：

Given a feature mapping Φ , can we find a corresponding kernel function K computing the inner product in feature space?
Given a kernel function K, can we construct a feature space H (i.e., a feature mapping Φ) such that K computes the inner product in H?
默瑟定理（Mercer’s theorem）is the fundamental theorem underlying Reproducing kernel Hilbert spaces，它对上述两个问题给出了肯定的回答。