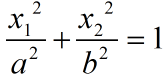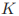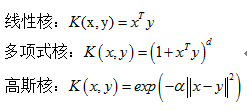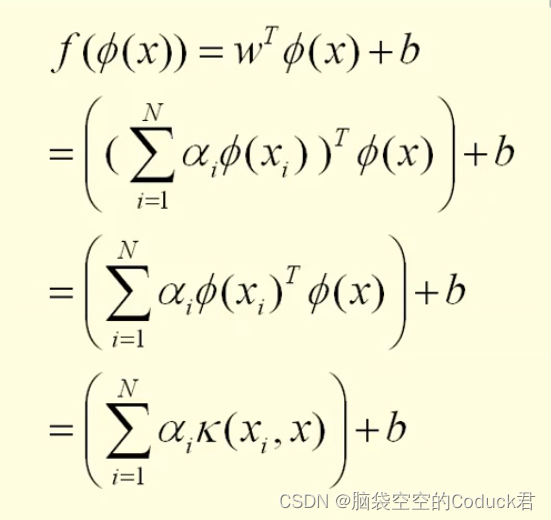最近对核方法比较有兴趣，想了解一下，在网上查阅了很多资料，感觉说的很晦涩，没有理解，于是查看了李政轩老师的课程，对其有了一定程度上的理解，本博客目的为了记录，也为了加深理解。

附上李政轩老师课程的地址：http://www.powercam.cc/slide/6552

为什么将低维空间转化为高维空间：

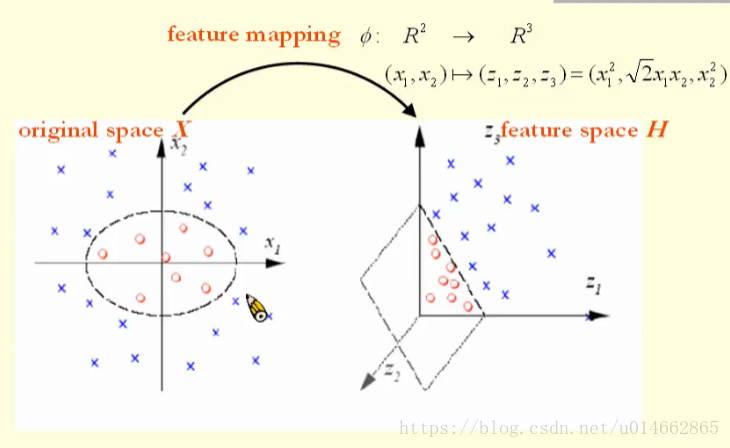
首先通俗理解一下核函数存在的意义，按照其他一些官方上的解释，核函数就是为了将低维空间上的点映射到高维空间上，是为了方便将不能用线性分割的数据转化成可以线性分割的数据（白话解释），如图所示：

如图所示，左面的图为为原空间，右面的图为映射后的空间，从图中也可以看出来，左面图要用一个椭圆才能将两个类别分割开来，而右面的图要用一个超平面就可以分割开，也如图上的共识所示，原空间点左边为（x1,x2）,经过某个函数或者某种计算方法，转化为特征空间上点坐标为(z1,z2,z3)，所以我们之前的说法是正确的，将低维空间转化到高维空间大概率可以对其中的点进行线性分割。

这样，我们第一步就理解了，就是在低维空间上的点通过某一函数转化为高维空间上，更有助于线性分类。那么我们开始理解下一步。

内积的意义：

在核函数中，会涉及到两个点的内积的计算，本节主要论述计算内积的意义。

两个点之间的内积是有一定意义的，可以通过两个点的内积计算距离和两个向量之间的角度，计算方法如下所示：

其中的字符代表着一个点。而根据两个点的距离，夹角等信息可以得到某些模型的超平面计算，讨论完内积的意义，下节将着重讨论核函数的重点内容。

核函数：

由于我们原特征空间是线性不可分的，所以要将原特征空间中的点x经过函数，转化到高维特征空间上，理论来讲，将低维空间转化到高维空间上，计算复杂度会变高很多，但是由于核函数的引用，巧妙的解决了这个问题。

我们需要优化的函数如下：

其中c为正负两类样本点连线的中点。如图所示：

w = (c+) -(c-),为红色线的向量

本函数计算绿色的线和红色线向量夹角，如果大于90度属于负类，否则属于正类。

计算过程如下：

其中的k(x,x1)，代表核函数，也就是高维空间两个点的内积。

所谓核函数，则是在原空间上两点内积的一个函数得到的，核函数样例如下所示：

将样本点从二维空间转化到三维空间：

从上述公式可以看出，核函数是一个可以用原特征空间上点内积的方式经过运算转化成高维空间点内积，而不必完全由高维空间上的点进行计算，从而达到降低运算复杂度的作用。