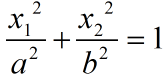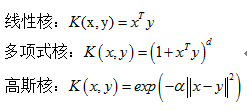使用.NET开发的Web应用程序部署到IIS上后，当有大量用户并发访问，用户在访问的时候可能会出现页面打开慢或无法打开的情况，那么从服务器上的IIS上我们可以做以下调整，让应用支持10万级以内的并发访问。

1、调整IIS 应用程序池队列长度，由原来的默认1000改为65535，如下图所示：

2、调整IIS的 appConcurrentRequestLimit 设置，找到C:\Windows\System32\inetsrv\config\applicationHost.config文件，如下图所示：

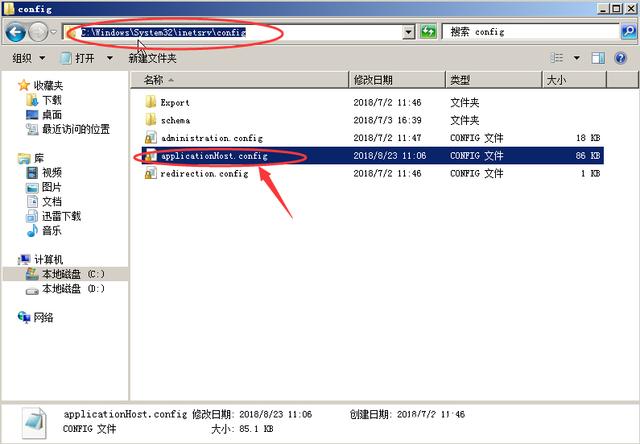
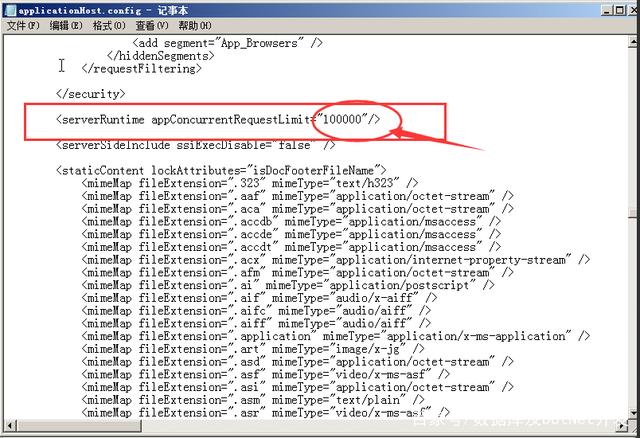
3、找到<serverRuntime/>配置节，由原来的默认5000改为100000，配置如下图所示：

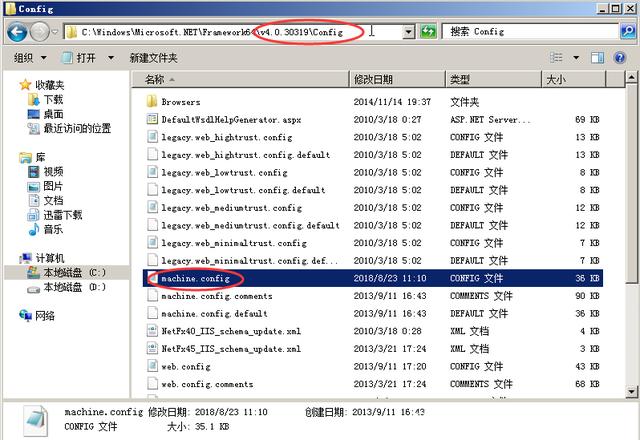
4、找到Framework的配置文件machine.config，如下图所示：

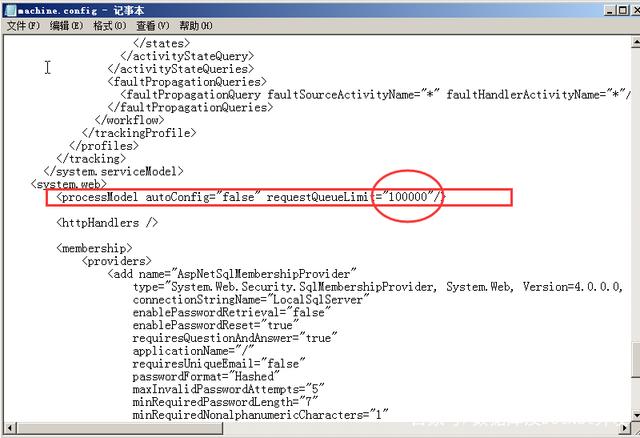
5、找到<processModel/>配置节，设置requestQueueLimit值为100000，如下图所示：

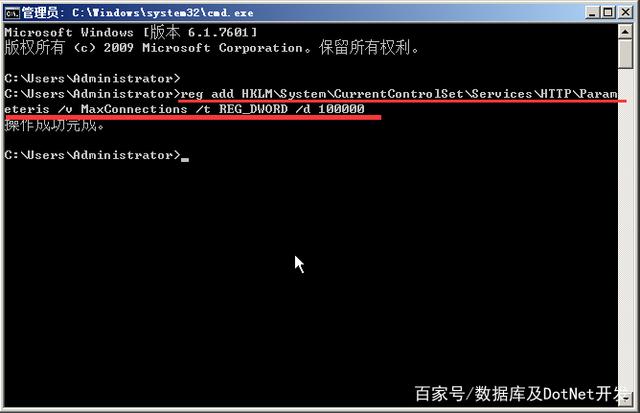
6、修改注册表，调整IIS 支持的TCP/IP连接数, 由原来的默认5000改为100000,只需要打开命令提示符，输入以下命令即可：

reg add HKLM\System\CurrentControlSet\Services\HTTP\Parameteris /v MaxConnections /t REG_DWORD /d 100000