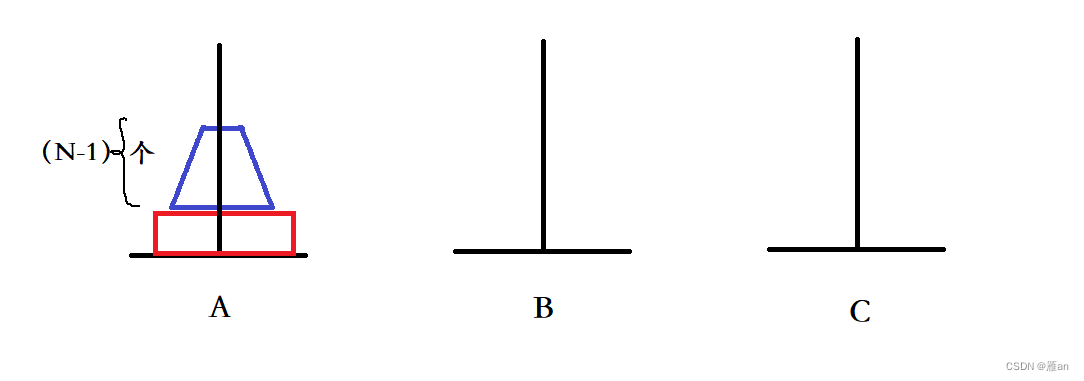目录
1.汉诺塔简介
2.汉诺塔分析
(1)寻找规律(采用物理中的参考系来进行推论)
①当n=1时
②当n=2时
③当n=3时
插曲:很多讲解汉诺塔博客,视频,很不严谨的地方,让初学者听不懂,很迷茫的问题根源!
④n=4时
⑤当n=5时
(2)探讨:三层以下汉诺塔是否也可以按上面规律进行求解?
(3)猜测结论
3.写出汉诺塔代码
4.汉诺塔移动次数分析(画图说明为什么是这个规律)
总结
1.汉诺塔简介
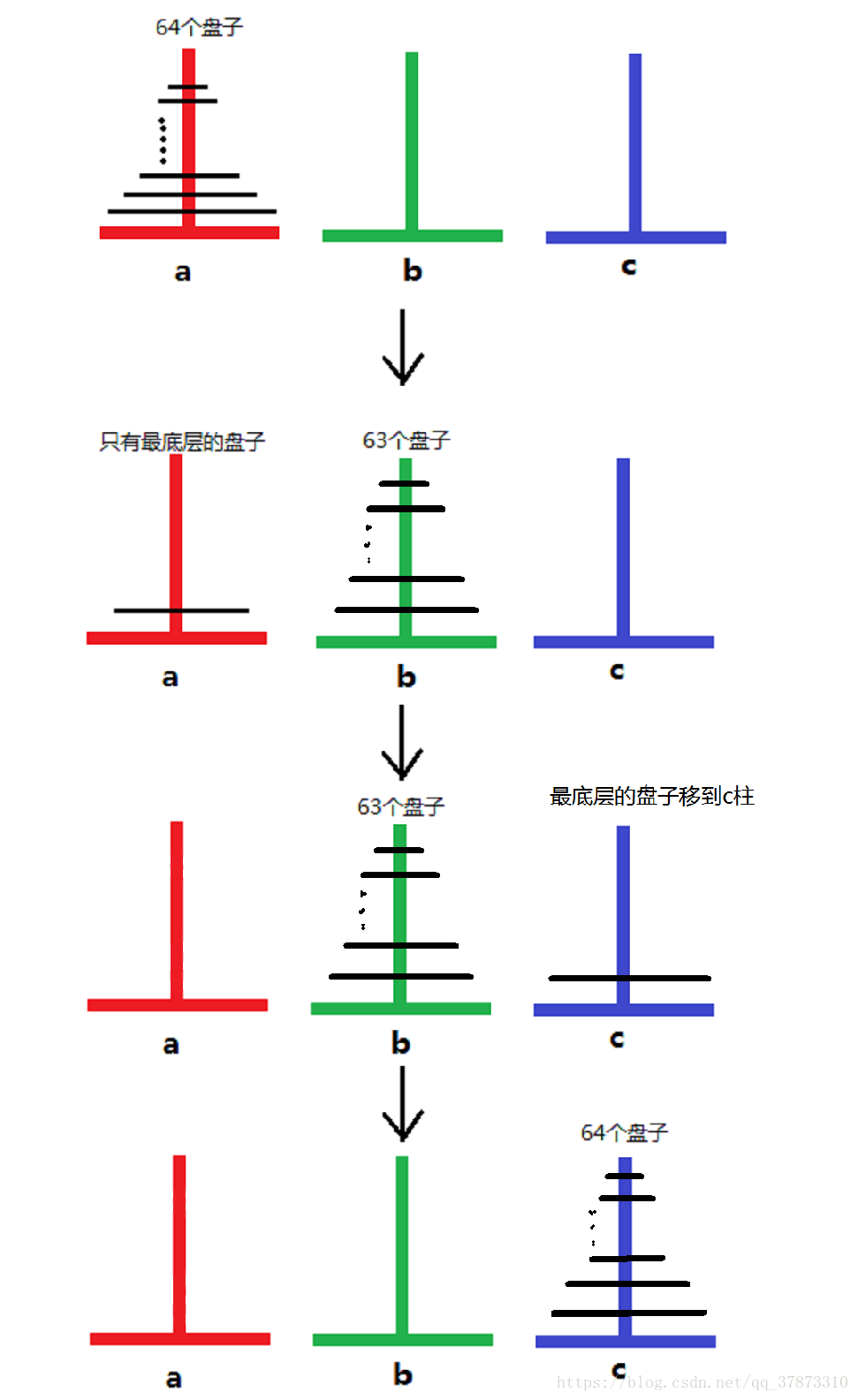
汉诺塔问题的源于印度一个古老传说的益智玩具。大焚天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照先大后小的顺序摞着64片圆盘。大焚天命令婆罗门把圆盘从下面按大小顺序重新摆放在另一根柱子上,并且规定在小盘子上不能放大盘子,在三根柱子之间一次只能移动一个盘子。
要把A柱上的盘子全部都移动到B柱上,并且要遵循以下规则:
1、一次只能移动原著最上面的一个盘子
2、小盘子上面不能放大盘子。
将n个盘子全部从A柱移动到C柱子上的步骤是什么?又需要多少次呢?
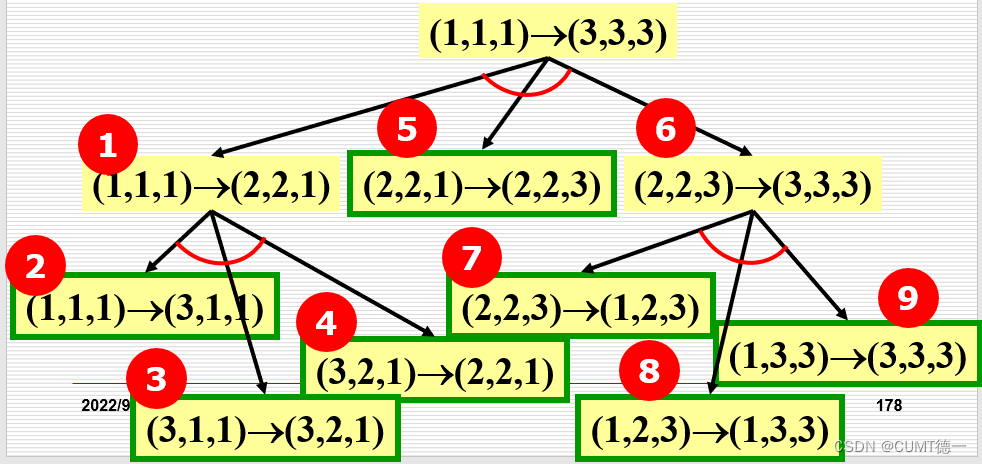
2.汉诺塔分析
这个问题是一个很神奇的问题,很多人感觉就是一脸懵逼,没思路,就算有思路,看懂别人写的,也还是感觉很奇怪,过一阵时间也会忘记,又不知道怎么写了。直到用递归但还是很迷茫。今天我们就来好好分析一下汉诺塔问题
相信大家高中时候都学过数学归纳法法吧,简而言之就是根据一下现象发现了规律,然后进行证明(第一项成立,假设第n-1项成立,推出第n项成立,则该规律成立),今天我们就采用数学归纳法来做这道题
(1)寻找规律(采用物理中的参考系来进行推论)
①当n=1时

那这太简单了,直接从A移动到C,我们为了方便将其记作A->C。
②当n=2时
这也很简单,无非就是把最上面的挪到B上,然后底层从A挪到C上,最后把B上的那个又给了C
我们记作A->B,A->C,B->C
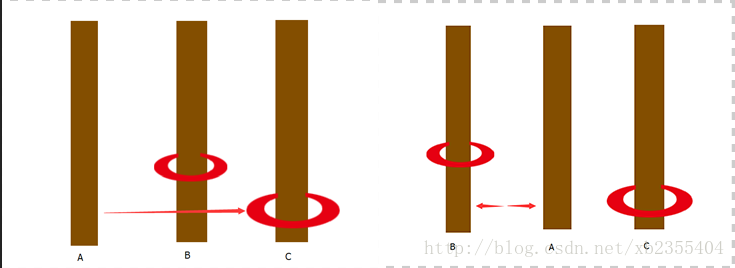
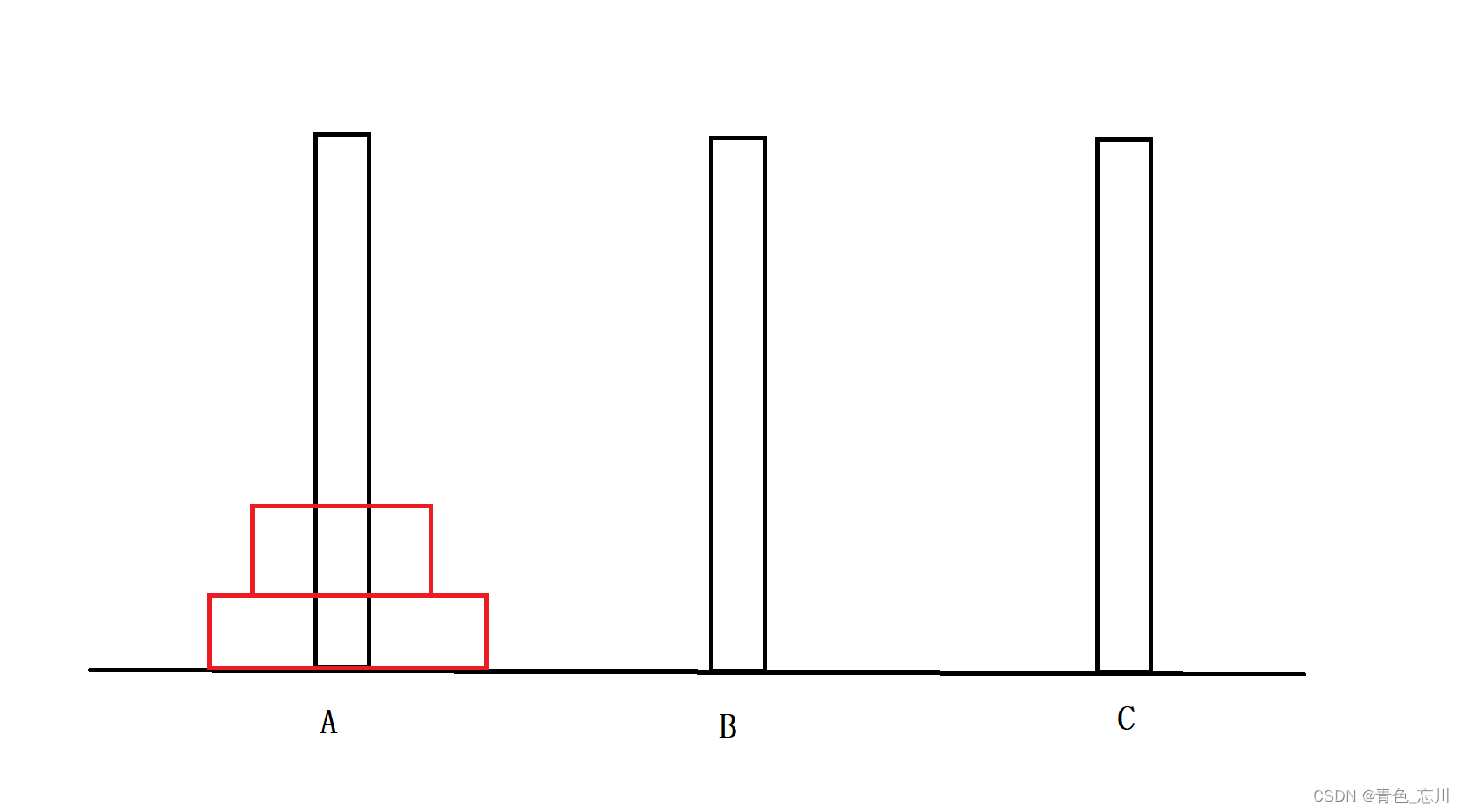
③当n=3时
似乎有点难度了?但是还在我们的接受范围内,我们只要认真一点还是可以做出来的,我们不妨用层数来进行计数吧,这样方便我们进行讨论
我们将A的第一层放到C上去
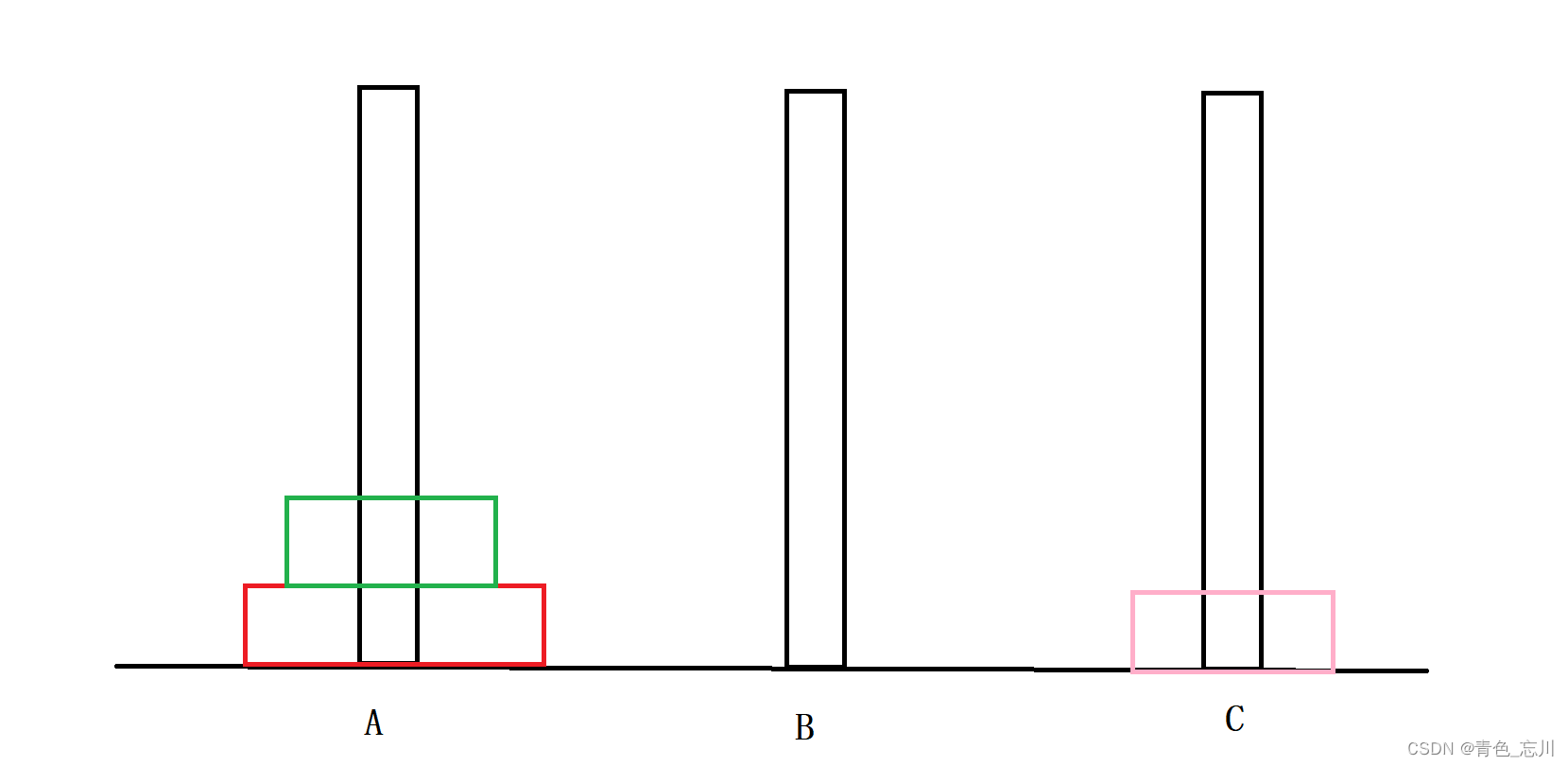
然后将绿色的放到B上去
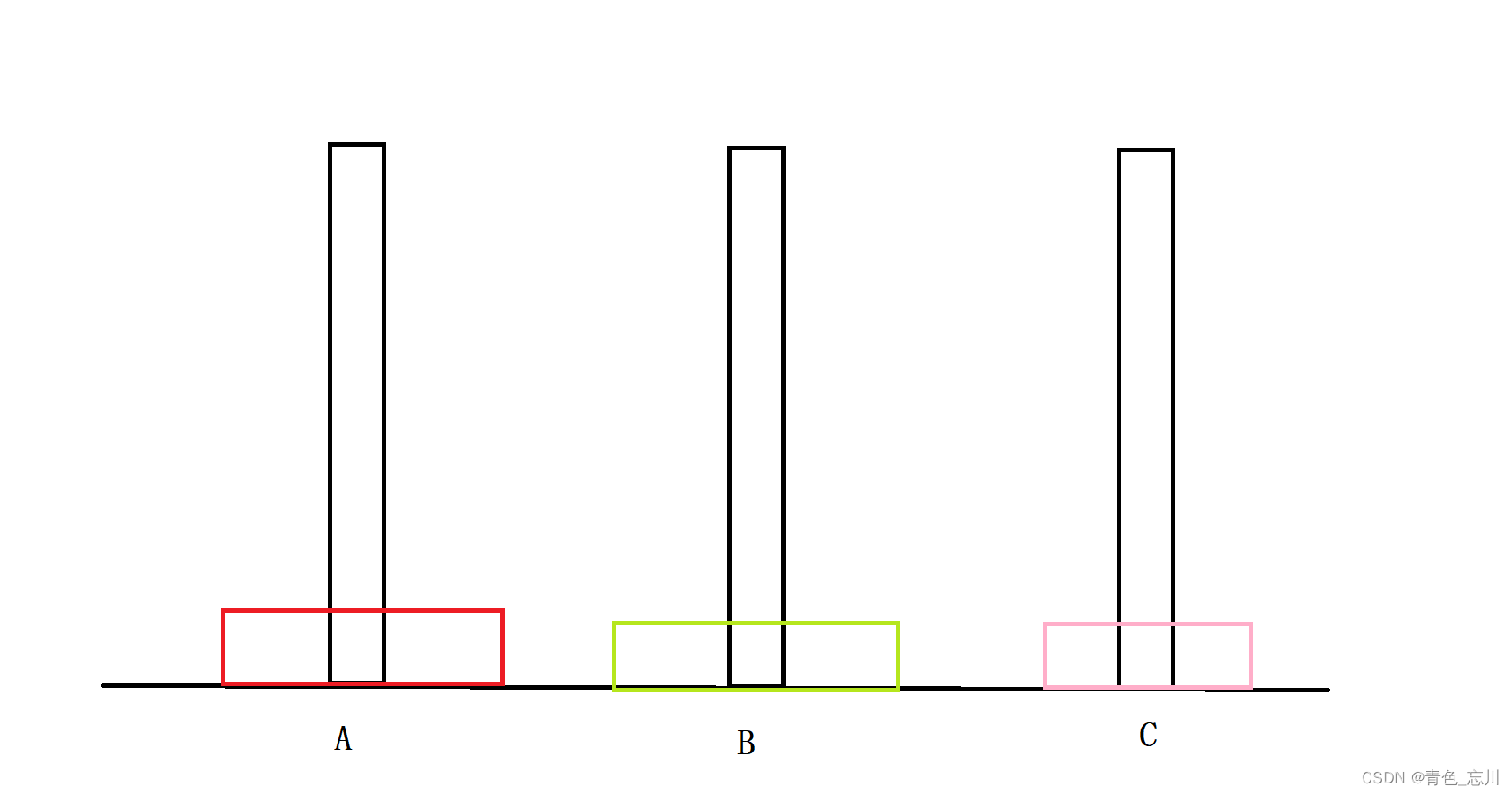
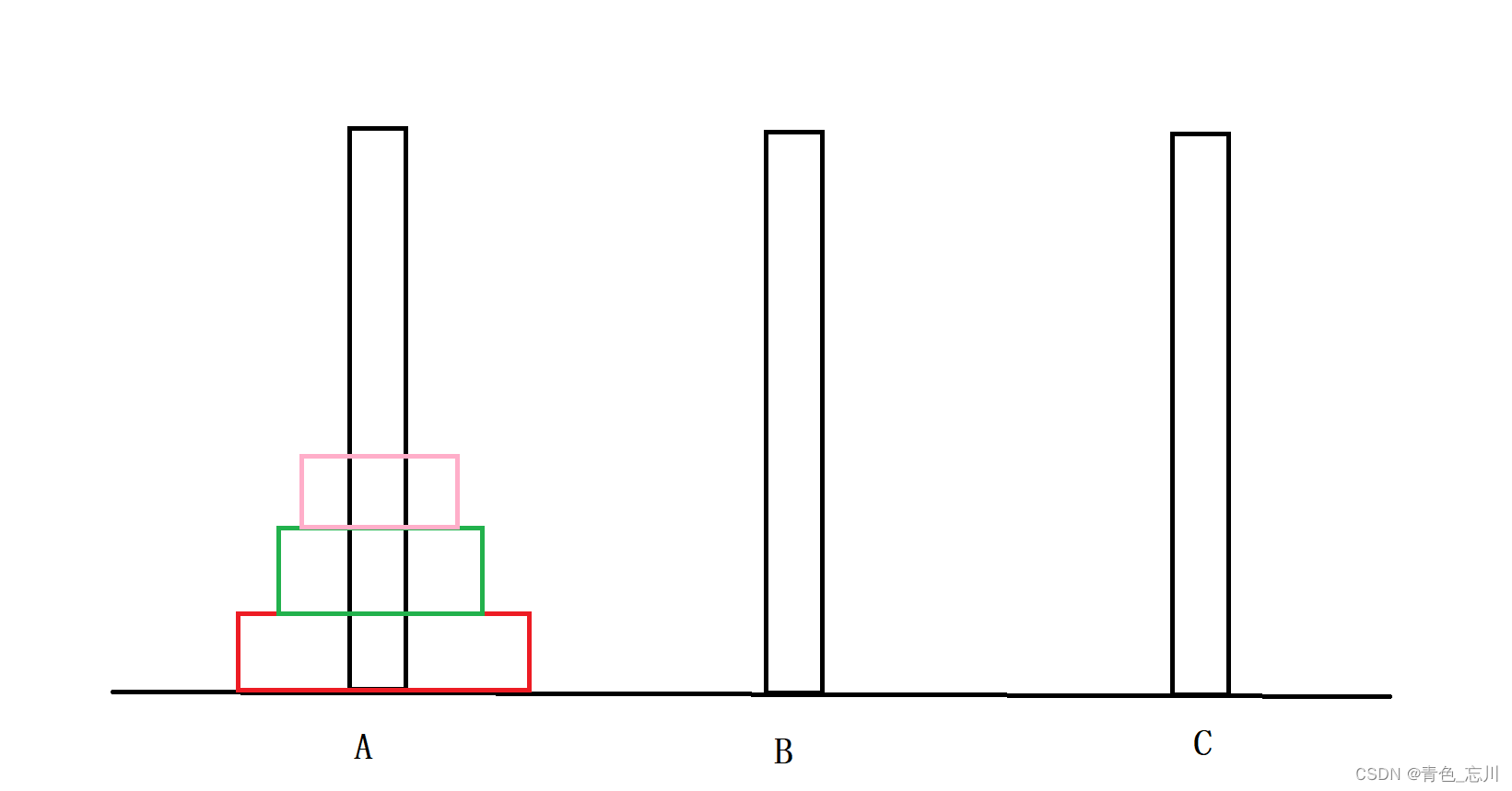
然后将粉色的放到B上去

将红色的放到C上去
现在问题就简单了啊,直接将粉色的挪到A上,然后绿色的挪到C上去,最后把粉色的挪到C上去,问题圆满解决
我们将此次问题解决记作:A->C,A->B,C->B,A->C,B->A,B->C,A->C
插曲:很多讲解汉诺塔博客,视频,很不严谨的地方,让初学者听不懂,很迷茫的问题根源!
到了这里,我相信90%的人仍然看不出任何规律,没关系!很正常,我们初中就知道,画出一个二次函数是五点法,要五个点才能画出一个函数图像,仅仅凭借三个点想要画出函数图像,那么初中老师绝对给你打零分。现在这才n=3,我们继续往下推。保证让你看到规律。
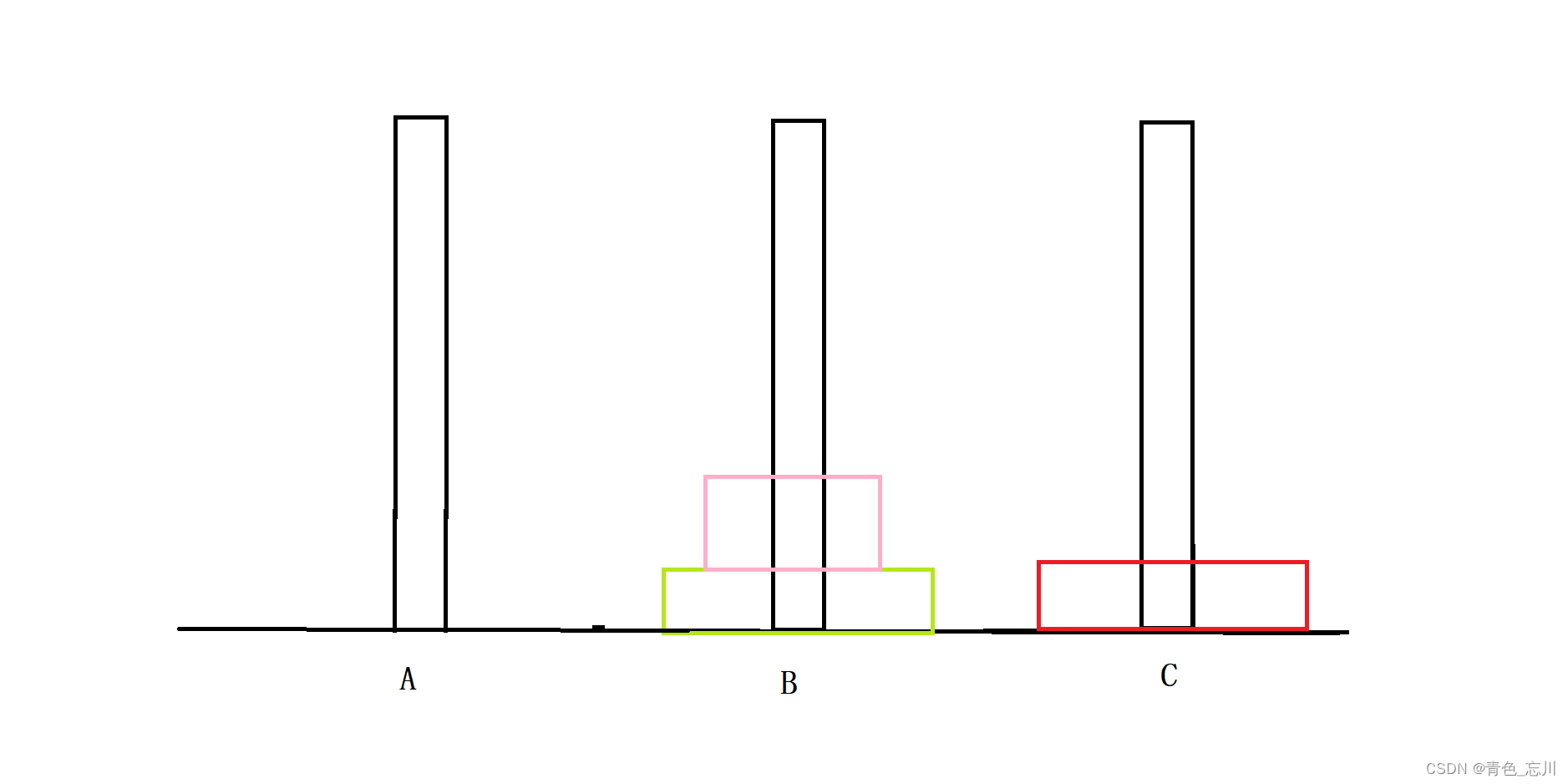
④n=4时
问题变得更加复杂了这个时候,回头看一下,我们一个方块,需要一次,两个方块需要,3次,三个方块需要7次,在高中时候我们都做个很多数列小题了,其中很多问题都是这样的,已经有前三次了,我们完全可以大胆推测第四次需要2的4次方-1次,也就是15次。当然这是我们的数学归纳假设,具体是否成立还需要严格证明。
我们已经预测第四次时候就有15次了,那我们就有可能得画15个图,15个步骤这太麻烦了,我们如何做呢?有没有更加简单的思考方式呢?我们说是有的,我们初中应该学过参照物的概念对吧,参照是相对而言的,根据这个物理概念,以及前三次的图解,你是否想到了什么?
没错,红色的方块是在最底层的,如果把他作为参照物的话,那么蓝色的,紫色的,绿色的,对于他们三个而言,红色的就是地面。对于他们三个而言,红色的根地面没有任何区别。这点相信大家都可以理解对吧
那好,那此时问题就转化为了我将上面三块给放到B上,然后将红色的那个参照物放到C上去,最后将B上的3块放到C上去,由于我红色的就是参照物,就相当于地面,所以这个问题就直接转化为两个三层汉诺塔问题。那么问题简直迎刃而解啊,三层汉诺塔简单啊!我们早已在n=3时候给出了具体的讨论步骤。
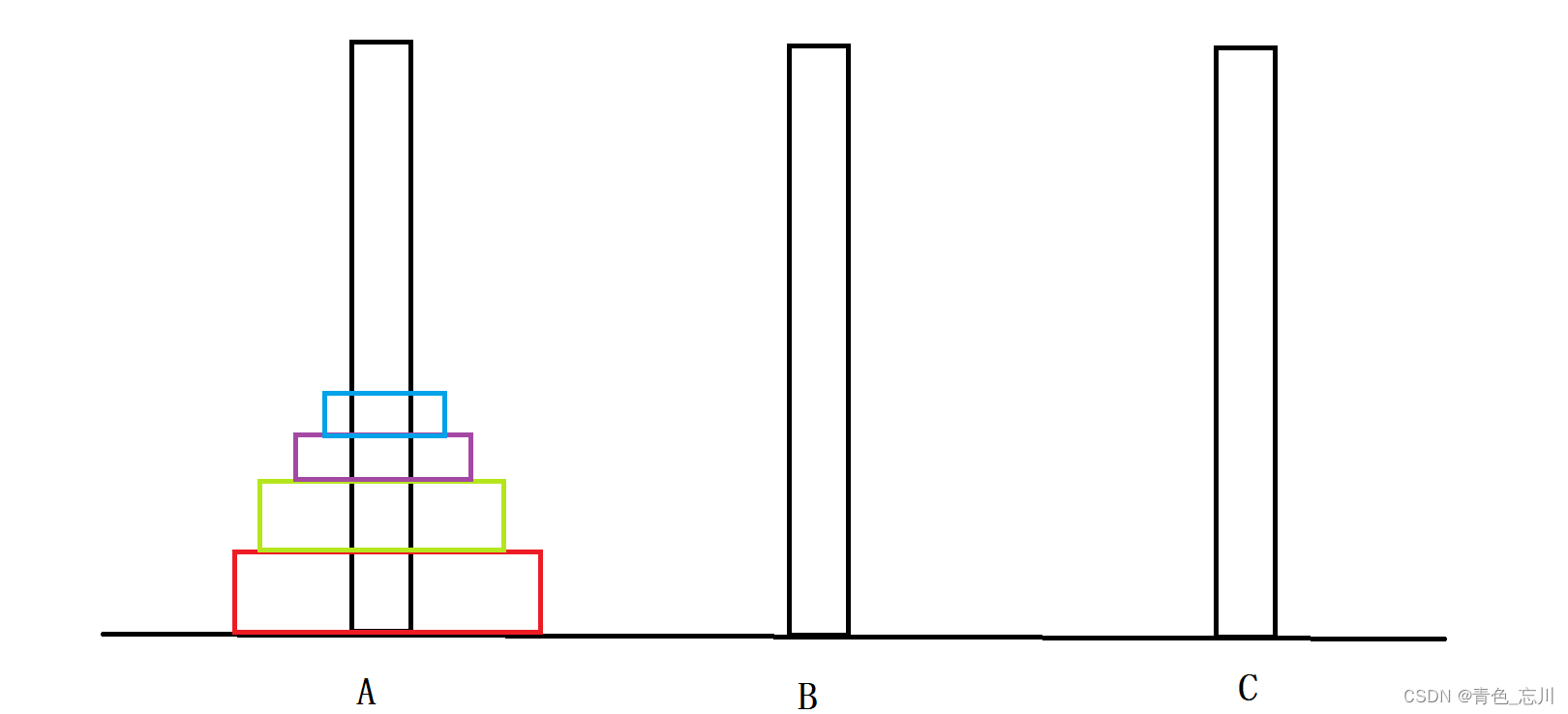
⑤当n=5时
当n=5时候,五层汉诺塔这问题就变得更复杂了。
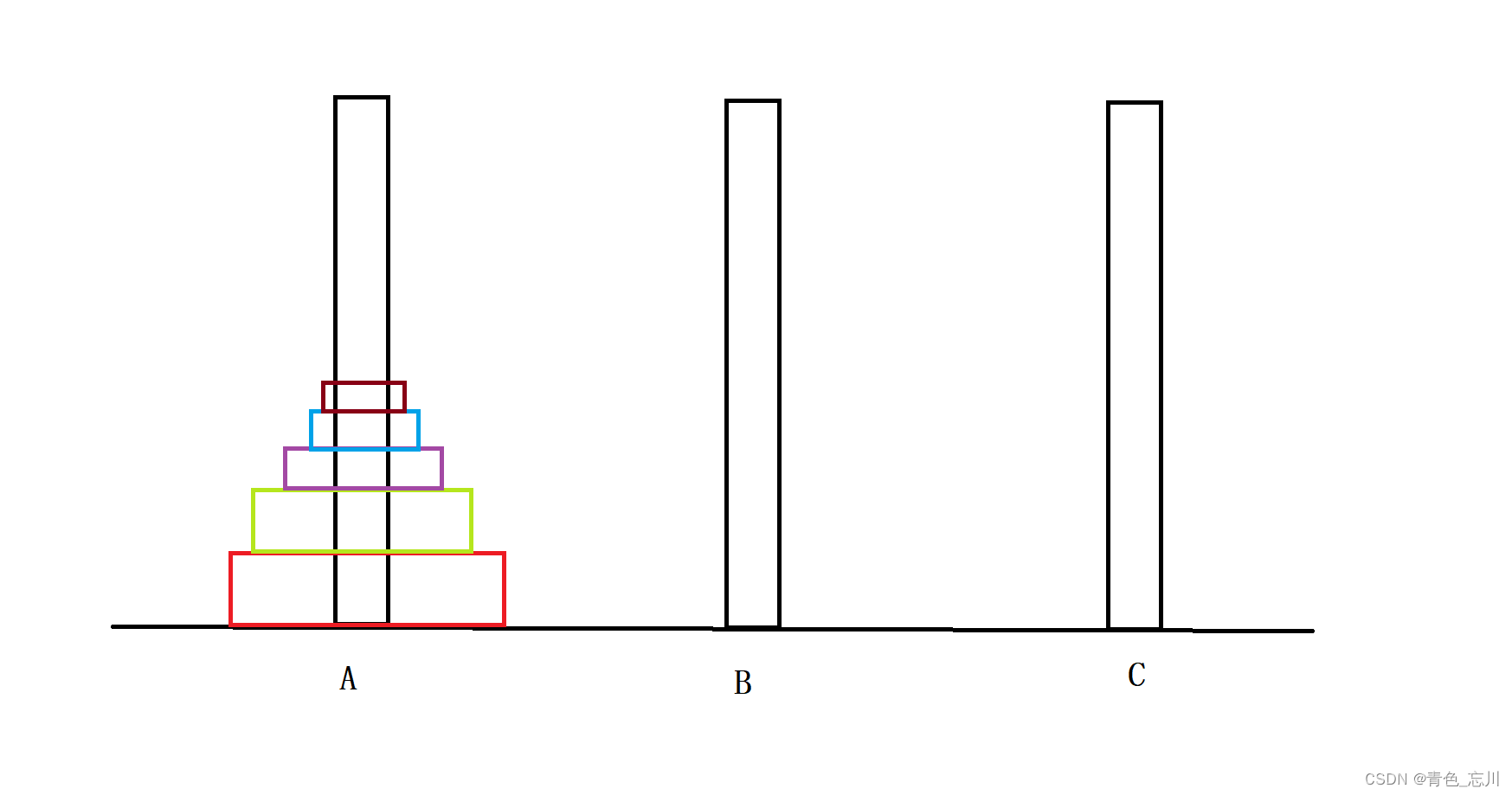
我们显然不能用正常的思路去进行求解了,但是,如果我们将红色作为参照物的话,那么对于上面四层而言,红色就相当于地面,我们就只需要先把上面四层挪到B上去,然后把红色挪到C上去,在进而想办法把B上的四层挪到C上去就可以完美的解决问题了。此时问题就转化为了,两个四层汉诺塔求解问题。而四层汉诺塔问题我们在上面已经得出结论了,他就相当于两个三层汉诺塔问题。
(2)探讨:三层以下汉诺塔是否也可以按上面规律进行求解?
我们发现五层汉诺塔居然等于两个四层汉诺塔问题求解。而四层汉诺塔又可以分解为两个三层汉诺塔求解,那我们似乎发现了什么规律,三层汉诺塔是否可以分解为两个二层汉诺塔呢?二层汉诺塔又是否可以分解为两个一层汉诺塔呢?
经过思考,我们发现好像确实可以,我们只要一直将最底层的汉诺塔视作参照物,无论是三层,还是两层,都可以分解为两个层数比他们小1的汉诺塔问题。
(3)猜测结论
经过上面的层次深度思考,我们可以大胆的猜测
对于任意的一个大于1正整数n,如果有一个n层汉诺塔问题,那么我们可以将之分解为两个n-1层汉诺塔问题求解。
事实上这个结论确实正确,因为任意一个n>2的正整数,都可以将最底层当作参照物,然后就可以分解为两个n-1层汉诺塔问题了
3.写出汉诺塔代码
那么分析完毕之后,我们就要写出汉诺塔的代码了
汉诺塔的函数该如何写呢?我们经过上面的分析得到
我们总的步骤其实就三步
当n>2时
1.将A上的n-1层通过C移动到B上
2.将A上剩余的(也就是最低层直接移动到C上)
3.将B上剩余的通过A移动到C上
当n=1时
直接从A移动到C上
根据上面的分析,我们得出,汉诺塔的主要应用函数其实就是将多少层的方块通过b从a移动到c上的问题,所以我们得出,这个汉诺塔函数得需要四个参数。
void Hanoi(int n,char a,char b,char c);
其中n为层数,a为起点,b为经过的中转点,c为目的地
我们可以得出n>2时候的汉诺塔的递推公式了。
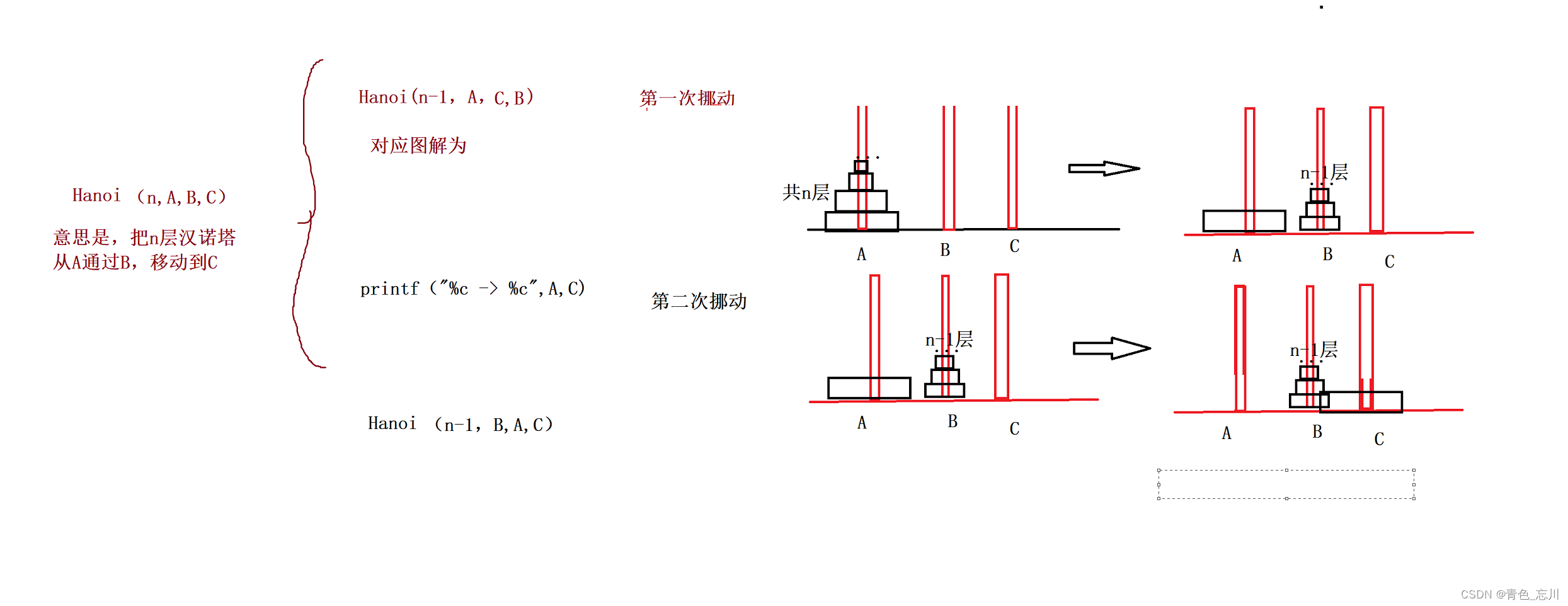
就是上面的三层移动
现在万事俱备,只欠代码了,代码安排一波
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
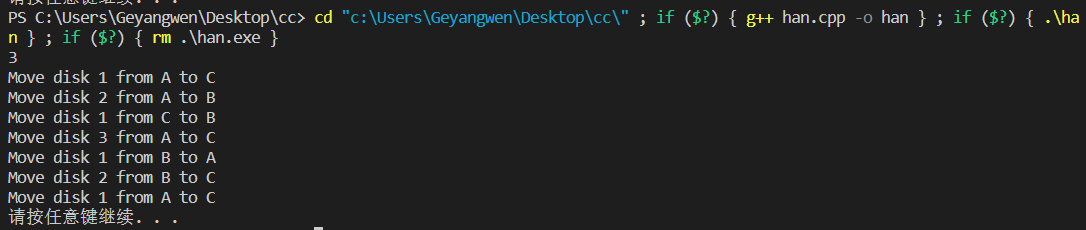
void Hanoi(int n, char a, char b, char c)
{if (n >= 2){Hanoi(n - 1, a, c, b);printf("%c -> %c\n", a, c);Hanoi(n - 1, b, a, c);}else{printf("%c -> %c\n", a, c);}
}
int main()
{int n = 0;scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');return 0;
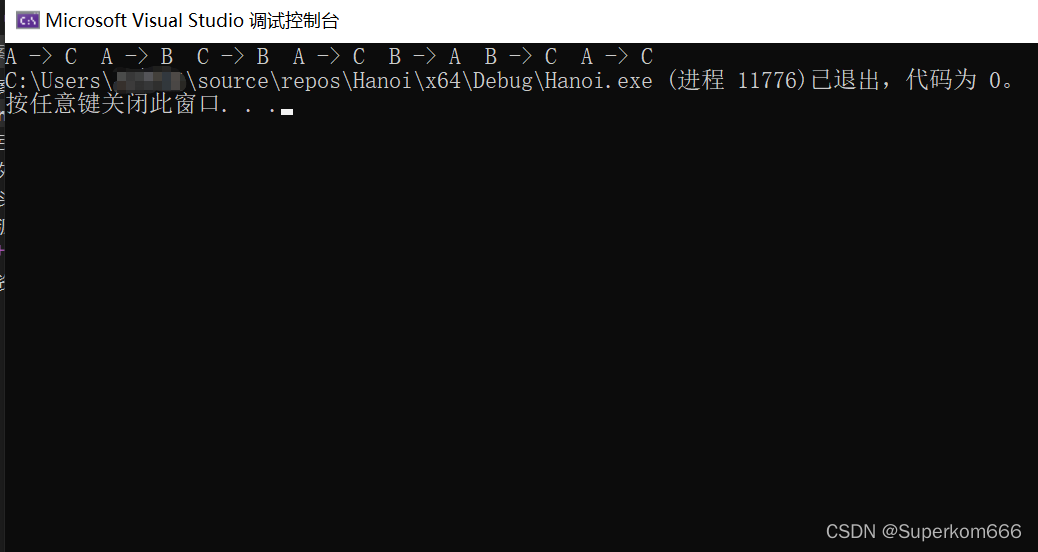
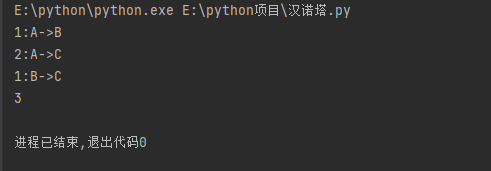
}我们验证一下,n为1,2,3,4,5时候的移动步骤
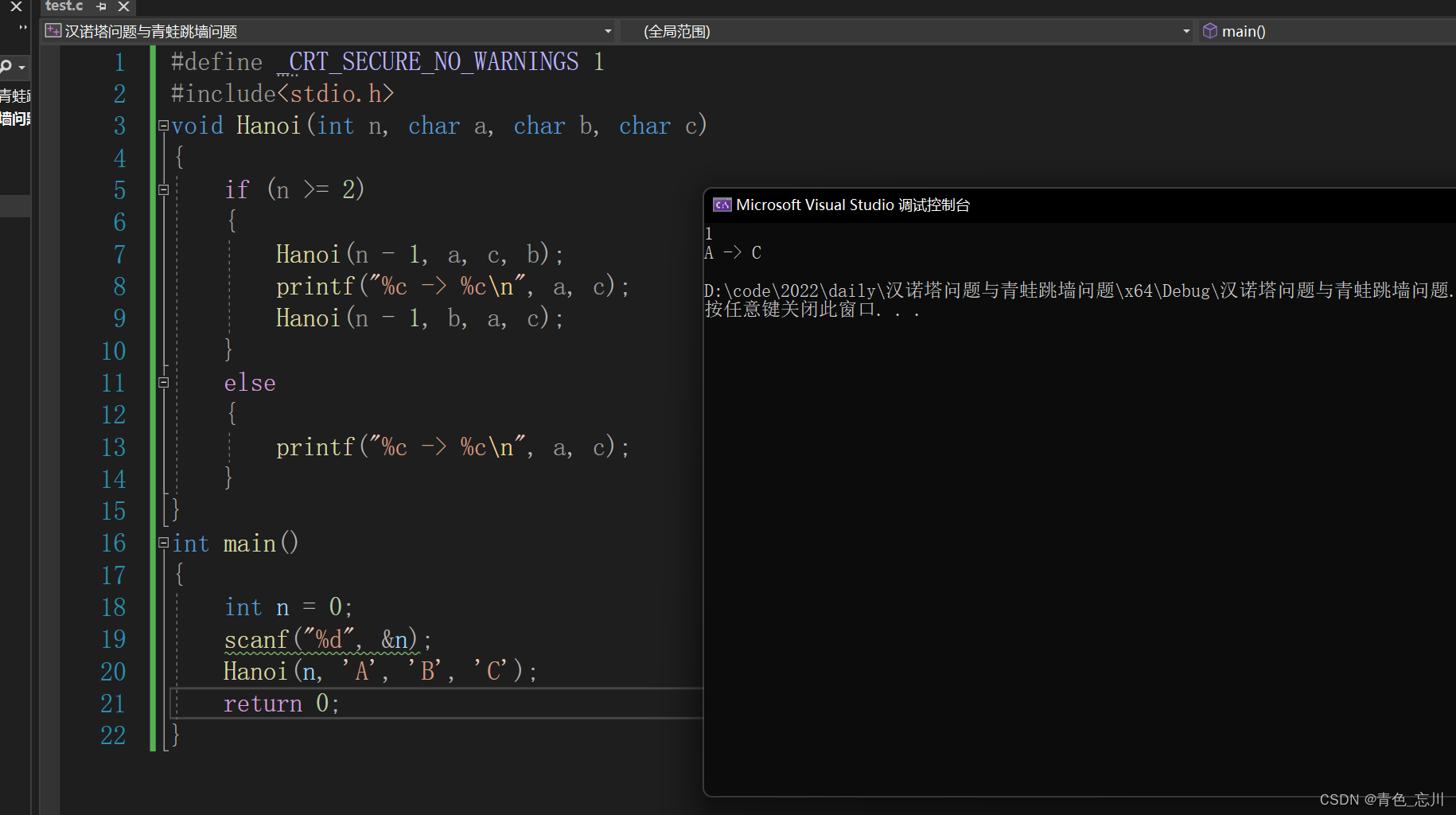

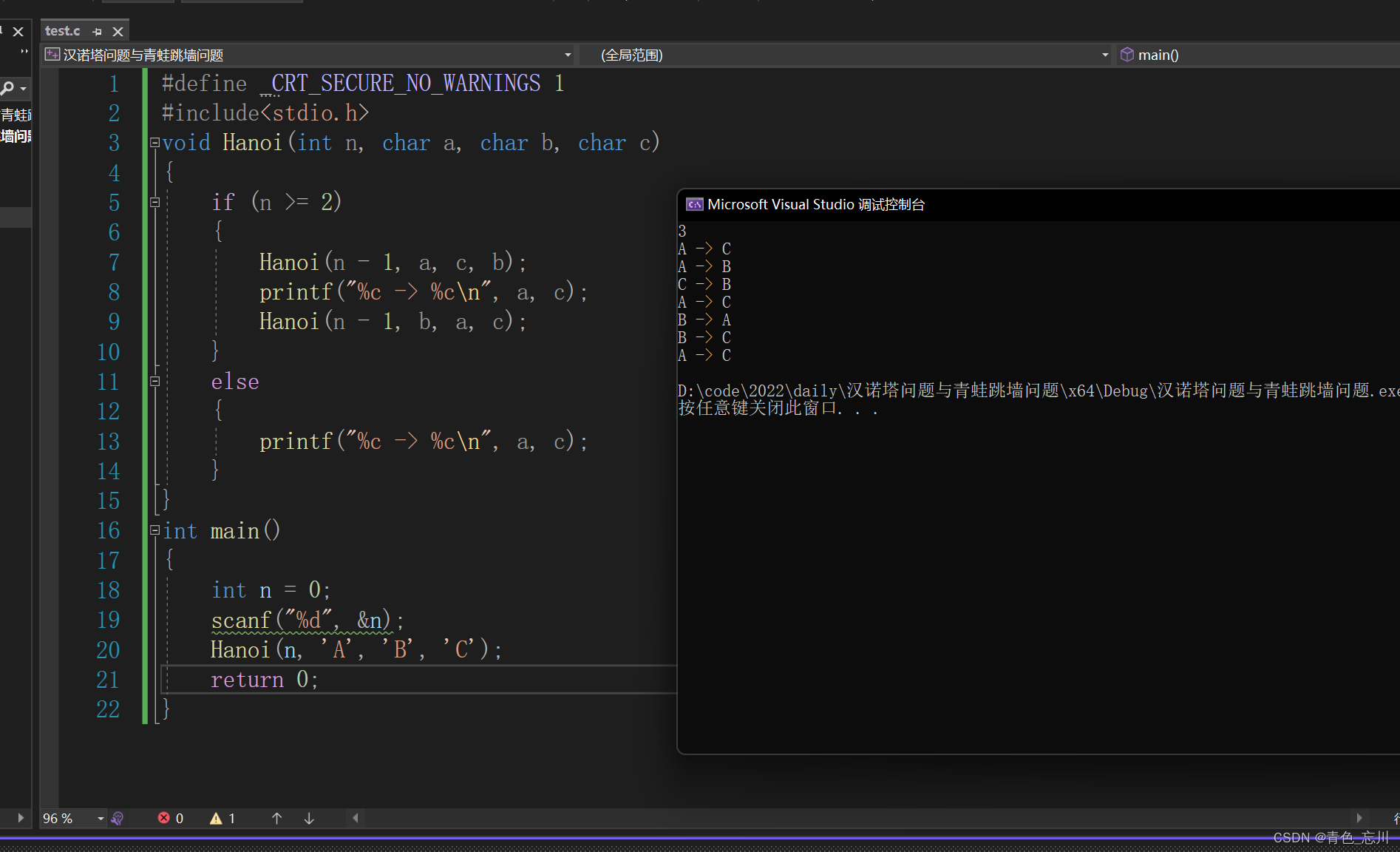
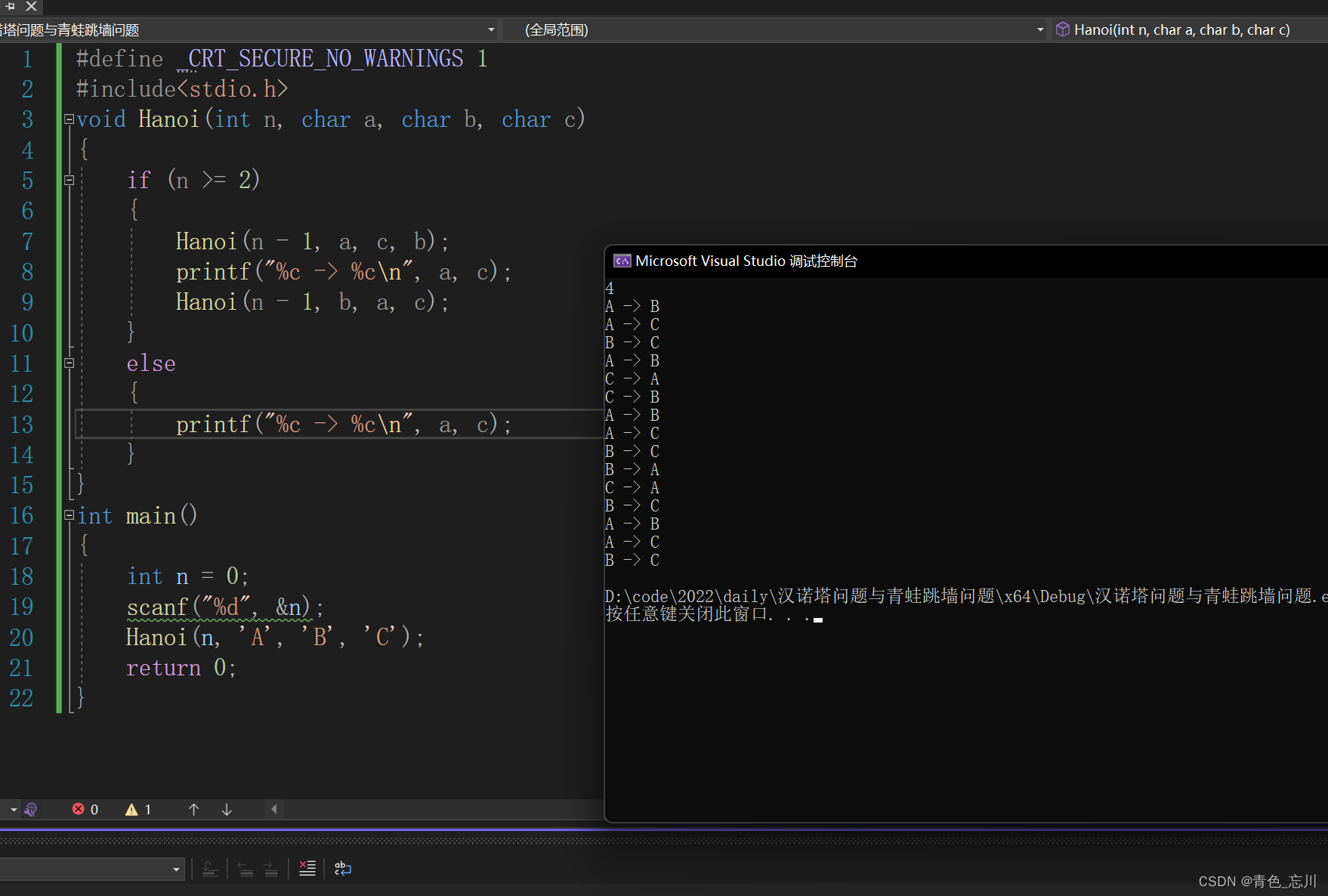

可见全部跟我们上面步骤一一吻合,并且我们在先前预测的第四层是15步,果然是正确的。接下来来详细探讨一下汉诺塔的次数分析
4.汉诺塔移动次数分析(画图说明为什么是这个规律)
在上文中我们大胆预测了规律是2的n次方-1,果然前五条全部满足
事实上我们可以用数学来证明一下这个次数。
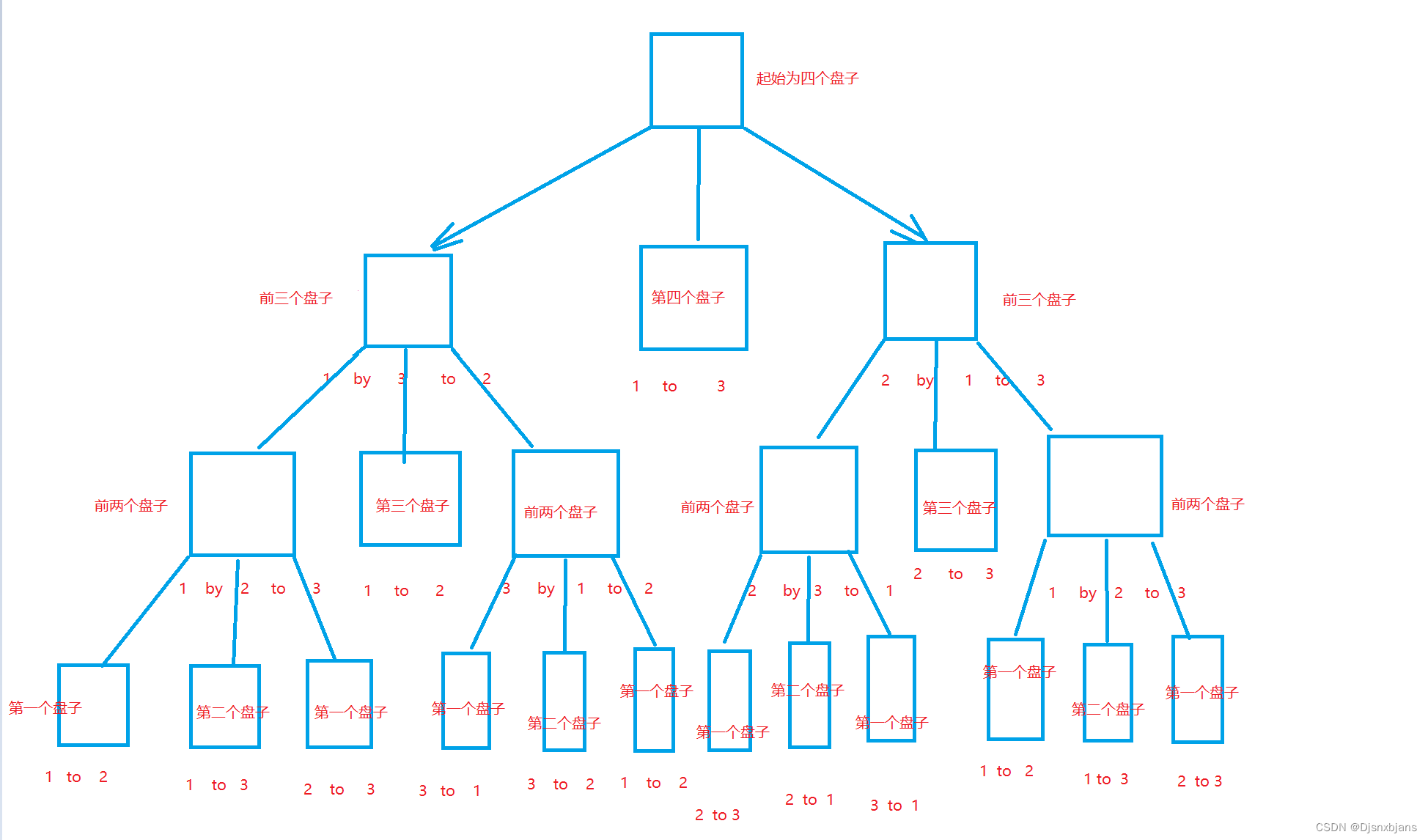
我们根据之前汉诺塔分解的思路画一个图

n层需要执行n-1层的次数+n-1层的次数+1次
这样每次进行分解,知道分解到1的时候就是1了
由于每一层会裂变为2个次一层,加上1,所以由数学的经过严格推理,求第n层的通项公式可得。
第n层的通项公式为2的n次方-1。(推理过程就不在这里讨论了,因为这已经是数学的知识了。不在本小节的讨论范围内)
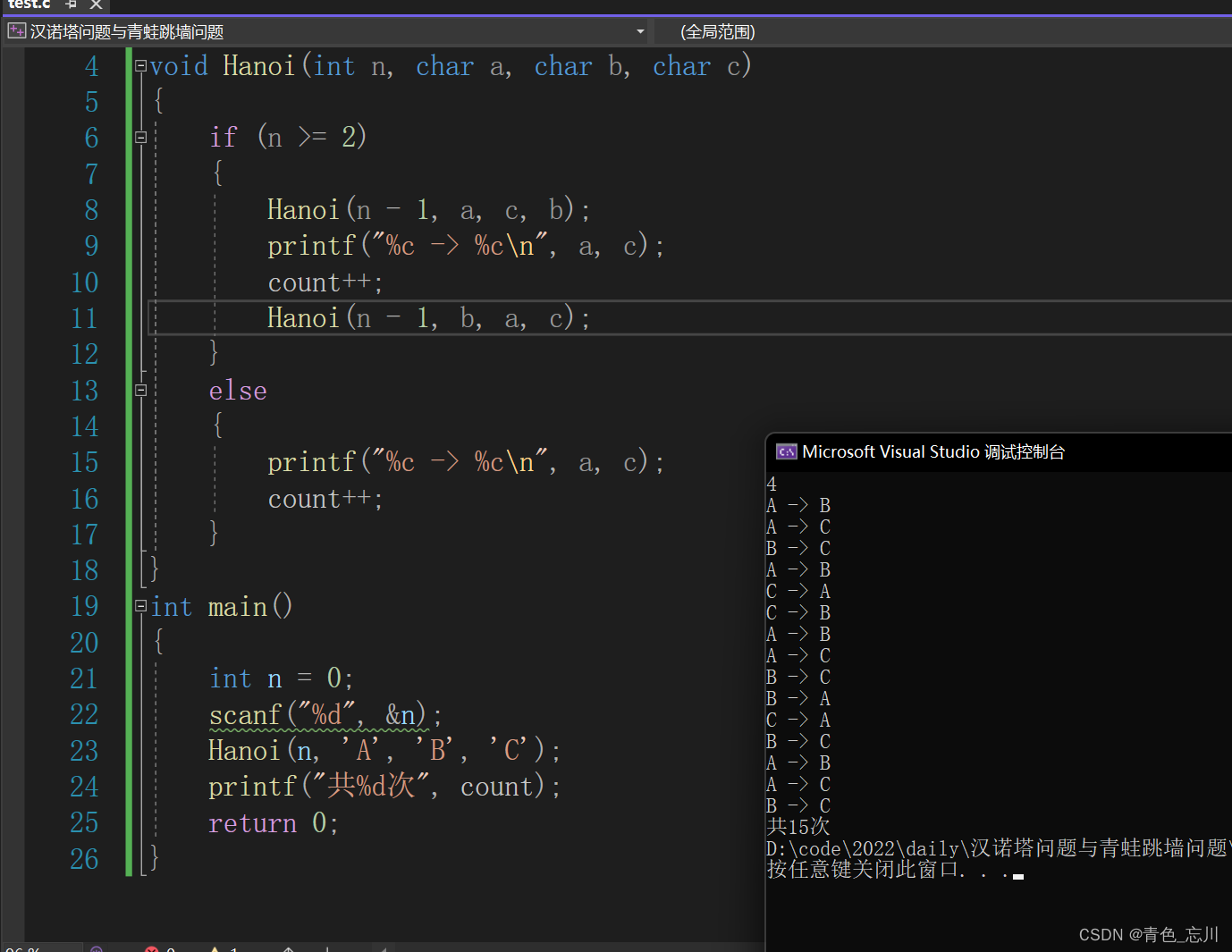
当然我们也可以加上一个计数器,去统计最终的次数,代码实现如下所示
int count = 0;
void Hanoi(int n, char a, char b, char c)
{if (n >= 2){Hanoi(n - 1, a, c, b);printf("%c -> %c\n", a, c);count++;Hanoi(n - 1, b, a, c);}else{printf("%c -> %c\n", a, c);count++;}
}
int main()
{int n = 0;scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');printf("共%d次", count);return 0;
}
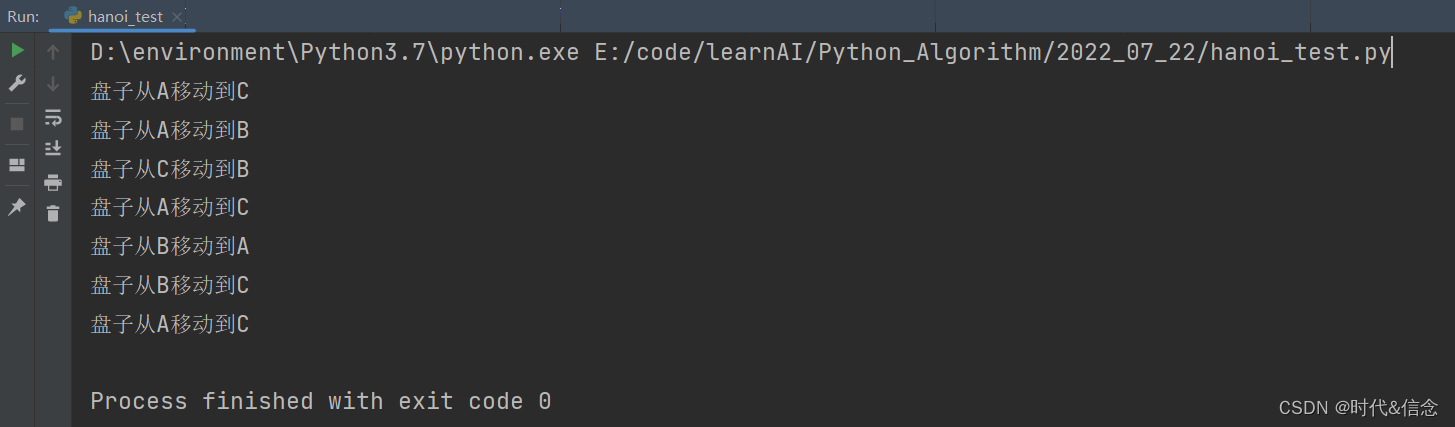
也可以每一行都打印这是第几次步骤
代码实现如下
#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
int count = 0;
void Hanoi(int n, char a, char b, char c)
{if (n >= 2){Hanoi(n - 1, a, c, b);count++;printf("第%d次:%c -> %c\n", count,a, c);Hanoi(n - 1, b, a, c);}else{count++;printf("第%d次:%c -> %c\n",count, a, c); }
}
int main()
{int n = 0;scanf("%d", &n);Hanoi(n, 'A', 'B', 'C');printf("共%d次", count);return 0;
}运行结果为
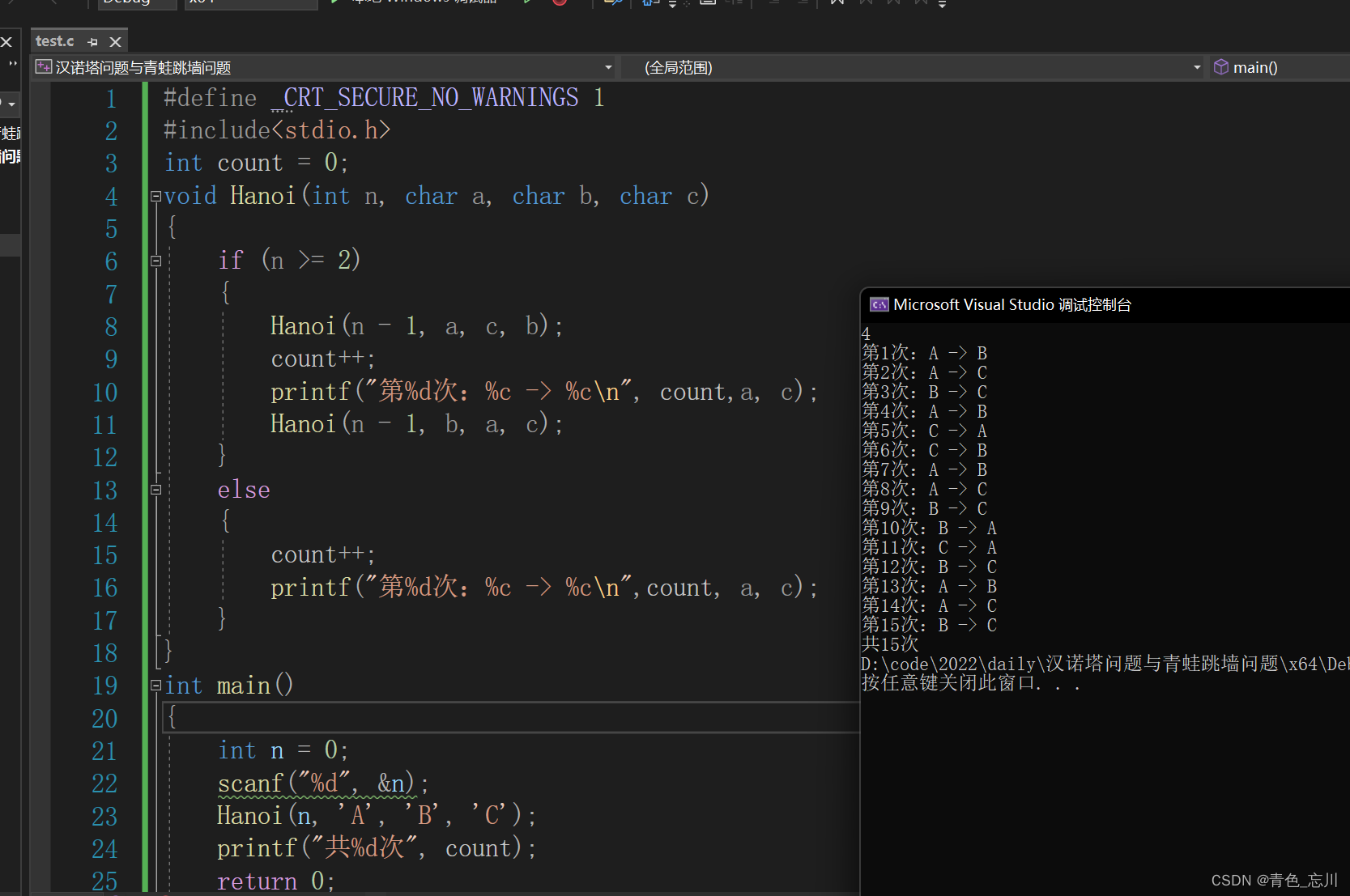
总结
本节主要讲解了汉诺塔问题的各种疑难杂症,有太多太多的初学者对这个问题怎么学也学不懂,摸棱两可。一定要自己理解如何推出规律。从而获得一些独立解决问题的能力!而不是遇到不会的题直接从网上搜,看一些只贴答案的博客。
最后如果觉得本文不错的话,一定不要忘记点赞加关注哦!!!
预告:其实在文章中已经已经有一些隐藏信息了,你能找到下一节课会详细会讲解哪一个经典的题目吗?