---

---

前言

汉诺塔问题是一个古典的数学问题，本文主要和大家一起用c语言解决汉诺塔问题。

---

1. 导入汉诺塔问题

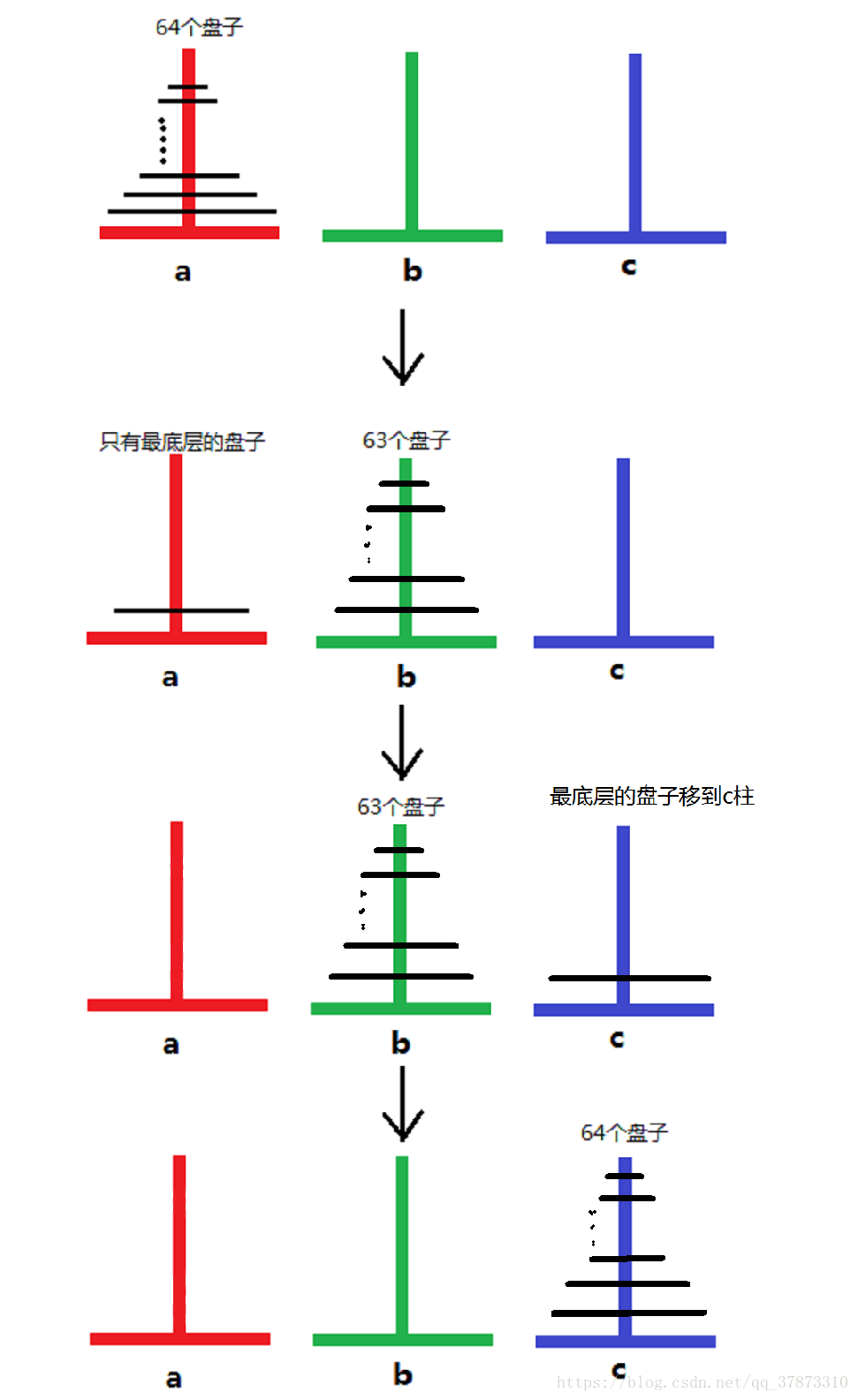
相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如下图)。

游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。

操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

2. 预备知识

汉诺塔问题是一个用递归方法解题的典型例子，所以我先了解一下函数的递归调用。

在调用一个函数的过程中又出现直接或间接调用该函数本身，称为函数的递归调用。例如：

int f(int x){int y,z;z = f(y); //在调用函数 f 的过程中，又要调用 f 函数   return(2*z);}

在调用函数 f 的过程中，又要调用 f 函数，这是直接调用本函数。
如果在调用 f1 函数过程中要调用 f2 函数，而在调用 f2 函数的过程中又要调用 f1 函数，就是间接调用本函数。

不过这两种递归调用都是无终止的自身调用。显然程序中不应该出现这种无终止的自身调用，而只应出现有限次数、有终止的递归调用，这可以通过if语句来控制，只有在某一条件成立时才继续执行递归调用；否则就不再继续。

3. 分析问题

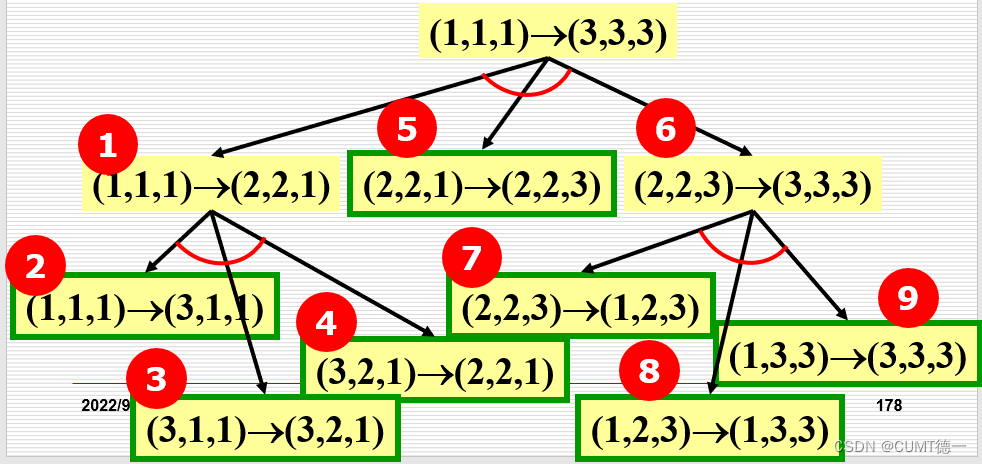
为了便于理解，先分析将 A 座上3个盘子移到 C 座上的过程：

1. 将 A 座上 2 个盘子移到 B 座上（借助 C）
2. 将 A 座上 1 个盘子移到 C 座上
3. 将 B 座上 2 个盘子移到 C 座上（借助 A）

其中第 2 步可以直接实现。第 1 步又可用递归方法分解为：

1.1 将 A 上 1 个盘子从 A 移到 C
1.2 将 A 上 1 个盘子从 A 移到 B
1.3 将 C 上 1 个盘子从 C 移到 B

第 3 步可以分解为：

3.1 将 B 上 1 个盘子从 B 移到 A
3.1 将 B 上 1 个盘子从 B 移到 C
3.1 将 A 上 1 个盘子从 A 移到 C

将以上综合起来，可以得到移动 3 个盘子的步骤：

A ->C
A->B
C->B
A->C
B->A
B->C
A->C

共经历了 7 步。
由此可以推出：移动 n 个盘子要经历 2ⁿ-1 步。如移动 4 个盘子需要经历 15 步，移动 5 个盘子需要经历 31 步，移动 80 个盘子需要经历 2⁸⁰-1 步。

很棒

我们已经知道 3 个盘子如何移动，n 个盘子的移动方法和上面 3 个盘子的移动方法相比，道理是一样的。采用递归的方法解决n 个盘子的移动问题。将 n 个盘子从 A 座移到 C 座可以分解为以下 3 个步骤：

1. 将 A 座上 n-1 个盘子移到 B 座上（借助 C）
2. 将 A 座上剩下的 1 个盘子移到 C 座上
3. 将 B 座上 n-1 个盘子移到 C 座上（借助 A）

上面第 1 步和第 3 步，都是把 n-1 个盘从一个座移到另一个座上，采取的办法是一样的，只是座的名字不同而已。为使之一般化，可以将第 1 步和第 3 步表示为：
将“one”座上 n-1 个盘移到“two”座（借助“three”座）。

4. 编程解决问题

#include <stdio.h>//定义move函数，将一个盘子从x座移到y座上 
void move(char x, char y)
{printf("%c-->%c\n",x,y);   //输出移盘方案。x,y代表A，B，C座之一，根据每次的不同情况分别取A，B，C代入 
}void hanoi(int n, char one, char two, char three) //将n个盘从one座借助two座，移到three座 
{if(n==1)move(one, three);else{hanoi(n-1, one, three, two); //将 A 座上 n-1 个盘子移到 B 座上（借助 C）move(one, three);//将 A 座上剩下的 1 个盘子移到 C 座上hanoi(n-1, two, one, three);//将 B 座上 n-1 个盘子移到 C 座上（借助 A）} } main()
{int m;printf("input the number of disks:");scanf("%d",&m);   //盘子的数量 printf("The step to moving %d disks:\n",m);hanoi(m,'A','B','C');}

接下来我们编译运行代码，并输入盘子的数量为 3，就可以输出移盘的方案：

input the number of disks:3
The step to moving 3 disks:
A-->C
A-->B
C-->B
A-->C
B-->A
B-->C
A-->C

---

最后，如有错误，还望指正， 如果有什么问题，可以在评论区留言，我会尽力为大家解决！