Java｜汉诺塔问题详解

article/2025/9/7 18:47:45

文章目录

- 汉诺塔问题：
- 编程要求：
- 解题过程：
- 代码实现：
- 总结

汉诺塔问题：

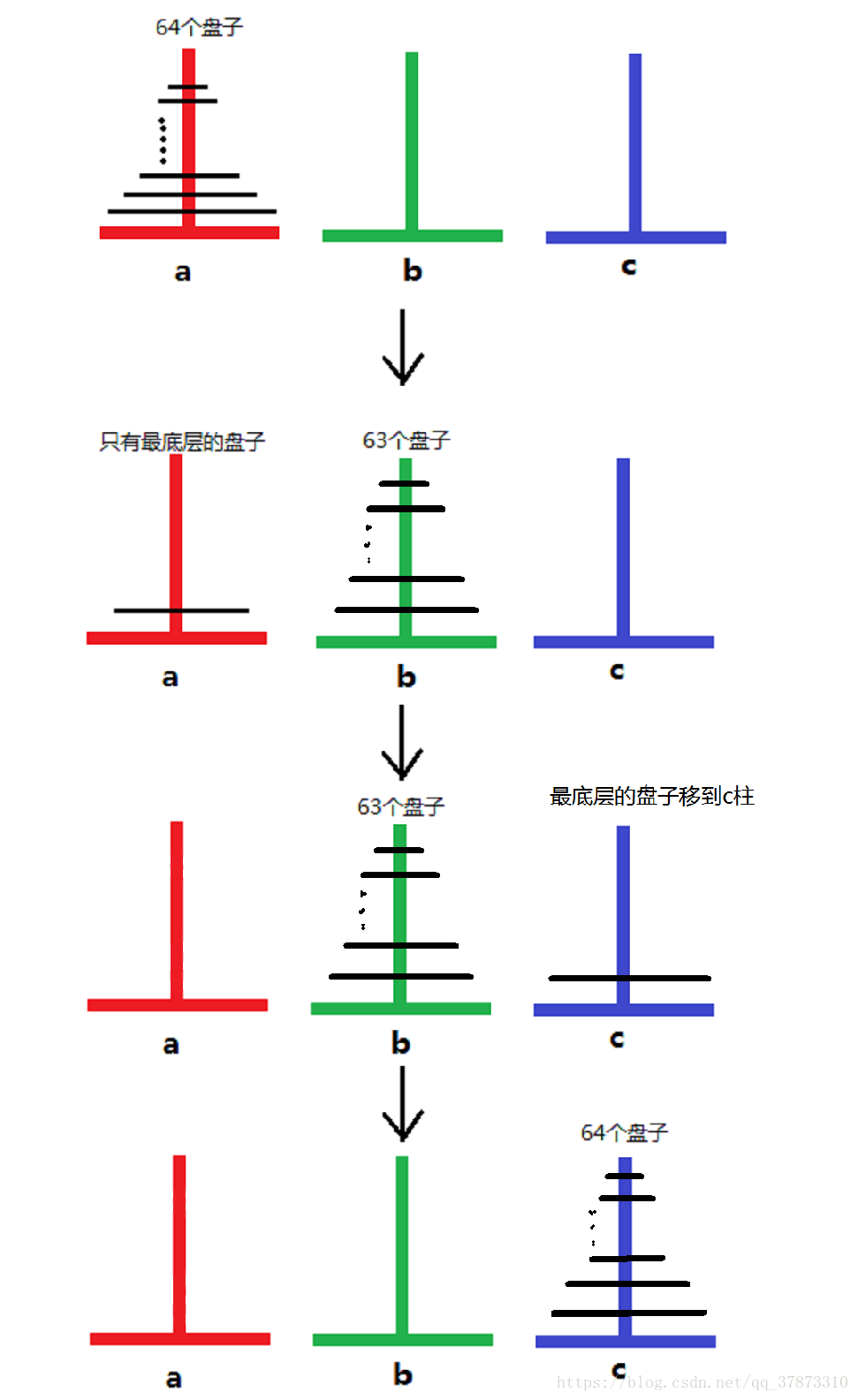
相传在古印度圣庙中，有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上，有三根杆(编号A、B、C)，在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标：把A杆上的金盘全部移到C杆上，并仍保持原有顺序叠好。操作规则：每次只能移动一个盘子，并且在移动过程中三根杆上都始终保持大盘在下，小盘在上，操作过程中盘子可以置于A、B、C任一杆上。

——来自于百度百科

编程要求：

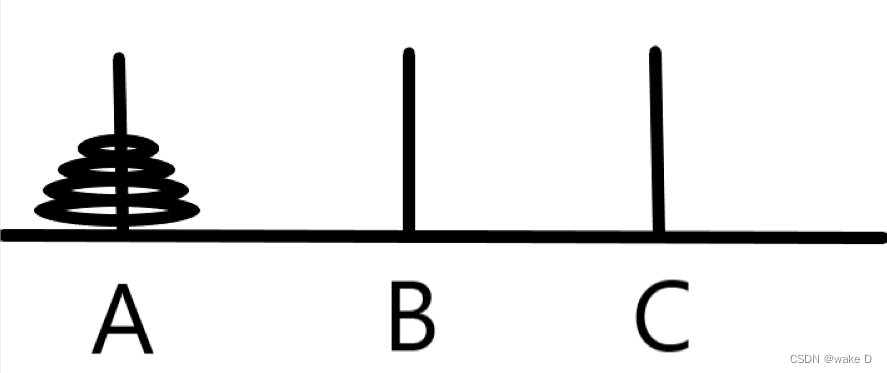
有A、B、C三根柱子，A为起始柱，B为辅助柱，C为目标柱，以及若干圆盘，圆盘按上小下大的顺序堆放在A柱上，从上到下依次为每一个圆盘标号为 1 到 n
输入圆盘数，要求将A柱的圆盘移动到C柱，一次只能移动一个，过程中可以任意使用三根柱子，但是要保证小圆盘始终在上
输出每一个圆盘每一步移动的过程，比如：1号圆盘从 A -> C

解题过程：

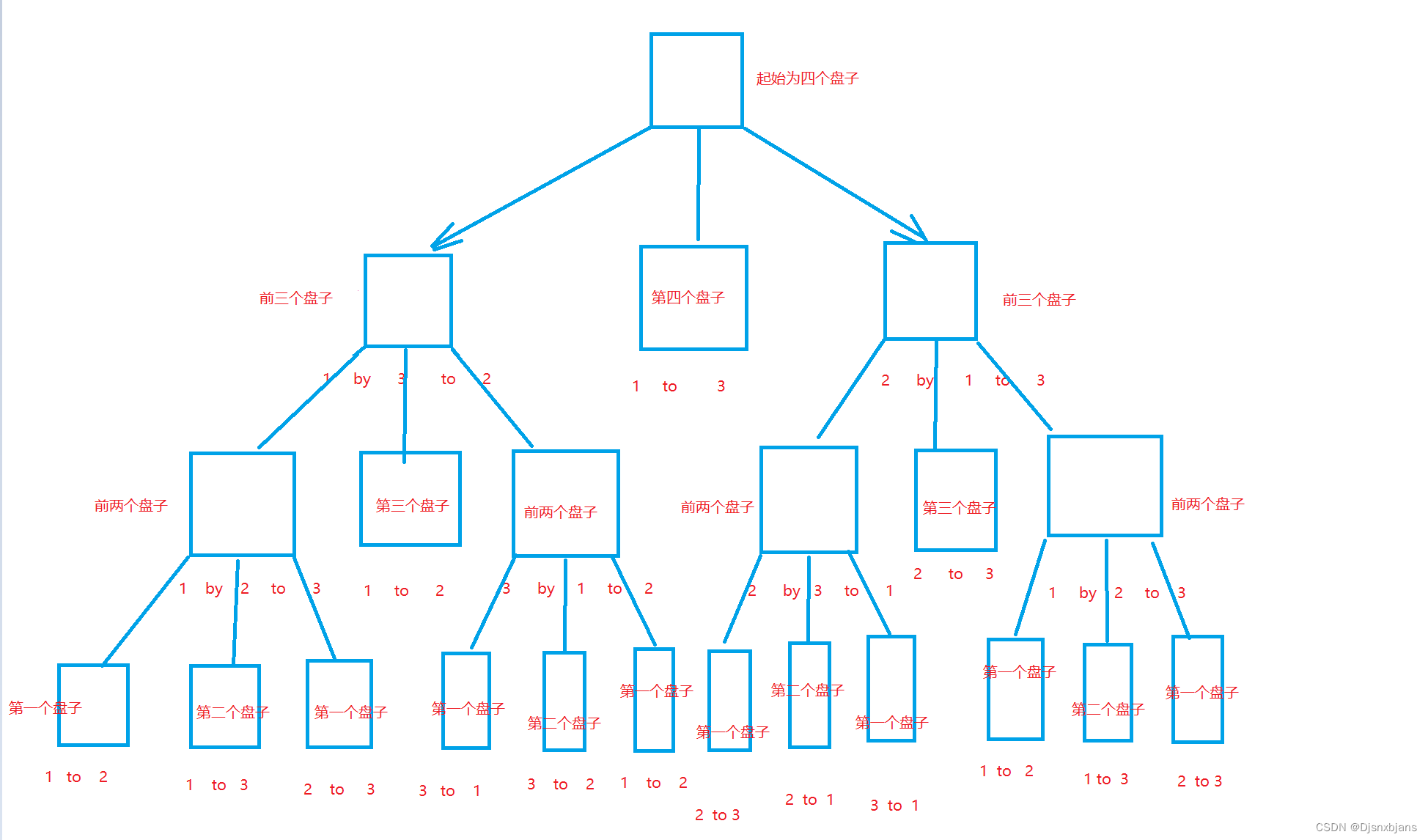
首先我们要知道，无论有多少个圆盘，最底下的圆盘 n 想要从起始柱移动到目标柱上，得先把除了 n 以外的圆盘移动到移动到辅助柱上

也就是说，如果有 n 个圆盘，我们想把第 n 个移到 C 上，得先把上面的 n-1 个移动到 B 柱，然后才能把第 n 个圆盘移动到C上

那么问题又来了，想把 n 上面的 n-1 个圆盘移动到 B 上，我们又需要把第 n-1 个圆盘上面的 n-2 个圆盘先移到 C 上，才能把第 n-1 个移到 B 上

……以此类推

直到我们拆分到只剩下1个的时候，我们可以直接把第 1 个圆盘移动到 B 或 C，具体让 1 号圆盘移动到哪一个让程序来实现

<img src="/Users/harley/Desktop/笔记图片/汉诺塔问题.jpg" alt="汉诺塔问题"

有了上面的想法做铺垫，我们就可以来思考，该怎么写代码了：

如果你理解了上面的内容，不难发现，移动 n 个圆盘，实际上就是先移动 n 上面的 n-1 个圆盘的问题

移动 n-1 个圆盘就是上就是移动 n-1号圆盘上面的 n-2个圆盘的问题……

实际上，只要是2个及2个以上的圆盘，其动作都是一样的，先把上面的圆盘移动到辅助柱，然后再把最底下的圆盘移动到目标柱上

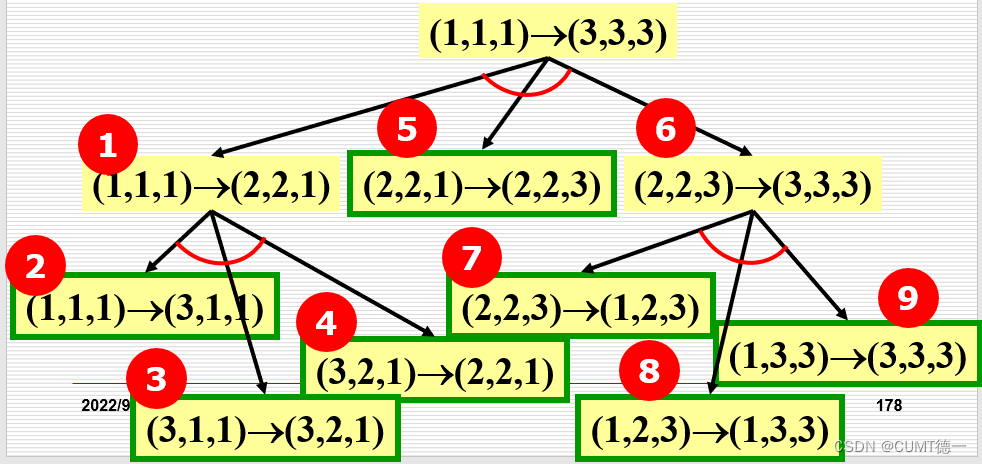
根据这点，我们就可以利用递归来实现这段代码

我们首先需要定义一个方法：

public static void fib(int num, char a, char b, char c) {if(num == 1) {System.out.println("第" + num + "个圆盘从" + a + "移动到" + c);}else {fib(num - 1, a, c, b);System.out.println("第" + num + "个圆盘从" + a + "移动到" + c);fib(num - 1, b, a, c);}
}

方法接收了需要移动的圆盘的个数 num，以及起始柱 a，辅助柱 b，目标柱 c，这里的变量 a 始终代表起始柱，变量 b 始终代表辅助柱，变量 c 始终代表目标柱

代码解析：

注意：a是个变量，存放起始柱，最开始为A柱，变量b、c同理

这个代码最底层只能实现把起始柱 a 上的最上面的圆盘移动到目标柱 c 上
而变量 a 中存放的就是起始柱，圆盘在移动的过程中，不可能一直都是 A 柱移到 C 柱
因此每次要移动的圆盘的起始柱、辅助柱以及目标柱都可能不一样

第一次进入方法的时候：

当你把 n 上面的 n-1 个圆盘移动到 B 柱上时，A是起始柱，C时辅助柱，B才是目标柱
接下来你要把第 n 个移动到 C 柱，此时不需要调用方法，直接从 a 移动到 c上
最后把 B 柱上的 n-1 个移动到 C 柱，此时 B 是起始柱，A 为辅助柱，C 是目标柱

如果以上的内容你都明白了，那么就没必要再往下深究 n-1 上面的 n-2 个圆盘的移动过程，因为真的很容易被绕晕

我们写出这个方法之后只需要想着如何调用他就好了，剩下的交给程序

代码实现：

public class Test {public static void main(String[] args) {Scanner in = new Scanner(System.in);System.out.println("请输入圆盘的数量");int num = in.nextInt();hanoi(num, 'A', 'B', 'C');//起始柱、辅助柱、目标柱默认为A、B、C}//汉诺塔问题实现//a存放起始柱，b存放辅助柱、c存放目标柱public static void hanoi(int num, char a, char b, char c){if (num == 1) {System.out.println("第" + num + "个圆盘从" + a + " -> " + c);}else{hanoi(num - 1, a, c, b);//借助c把第 num 个以外的圆盘从a移动到bSystem.out.println("第" + num + "个圆盘从" + a + " -> " + c);//把第num个从a移动到chanoi(num - 1, b, a, c);//借助a把第 num 个以外的圆盘从b移动到c}}}
//执行结果
请输入圆盘的数量
3
第1个圆盘从A -> C
第2个圆盘从A -> B
第1个圆盘从C -> B
第3个圆盘从A -> C
第1个圆盘从B -> A
第2个圆盘从B -> C
第1个圆盘从A -> C