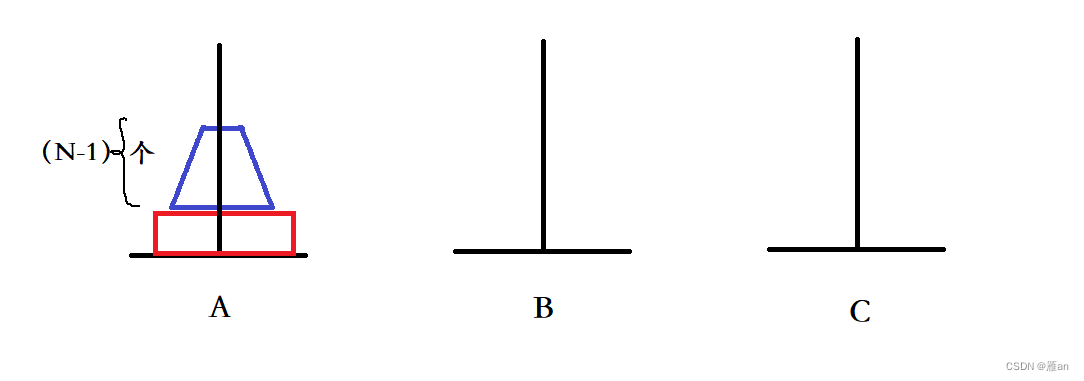前言:

大家好，又是再一次分享文章，我十分感谢各位能够点开这篇花费我颇多时间才解决的汉诺塔问题，接下来我就要分享一下自己的所思所想，希望能给各位带来一些不一样的收获吧。

提醒:

汉诺塔问题的本质是函数递归，而函数递归已经是我们现阶段学习的C语言函数内容的后期知识，所以各位要想了解汉诺塔问题，请先学习好与函数有关的一些基本与重要的知识，还请各位多多理解。

说明:

我认为了解一个东西最重要是重复的实践，所以大家想要更好的了解汉诺塔问题，可在4399小游戏中或以其他方式去玩一玩，一定会加深你的认知的。

1. 问题简述（以三层为例）

2. 背景

3. 数学思想

4. 执行过程的具体分析

(1) 过程简易分析(以三层为例)

(2) 思考

(3) 解答

(4) 递归说明

5. 整体代码及显示效果

6. 寄语

注意: 目录4.是整个汉诺塔问题最重要的部分，主要涉及了函数的递归问题，我会将每次的递归步骤在图纸上演示一遍（图有点丑，别嫌弃哈），以便大家更好的理解。我更希望如果各位真的想好好了解这个汉诺塔问题，就不要畏惧，其实并不难，认真看过程，我已经很详细地讲述我的理解了，希望能加深各位对汉诺塔问题的认识。

1. 问题简述（以三层为例）

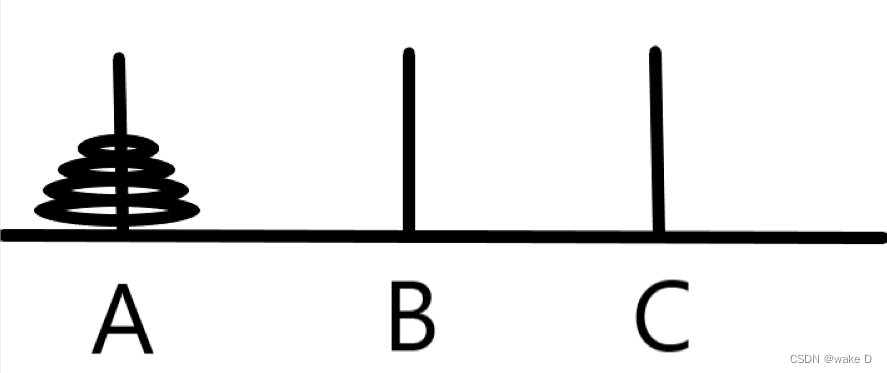
（1）有三根柱子A，B，C。A柱上有n个盘子

（2）每次移动一个盘子，小的只能放在大的上面

（3）将所有盘子从A杆经过B杆全部移到C杆上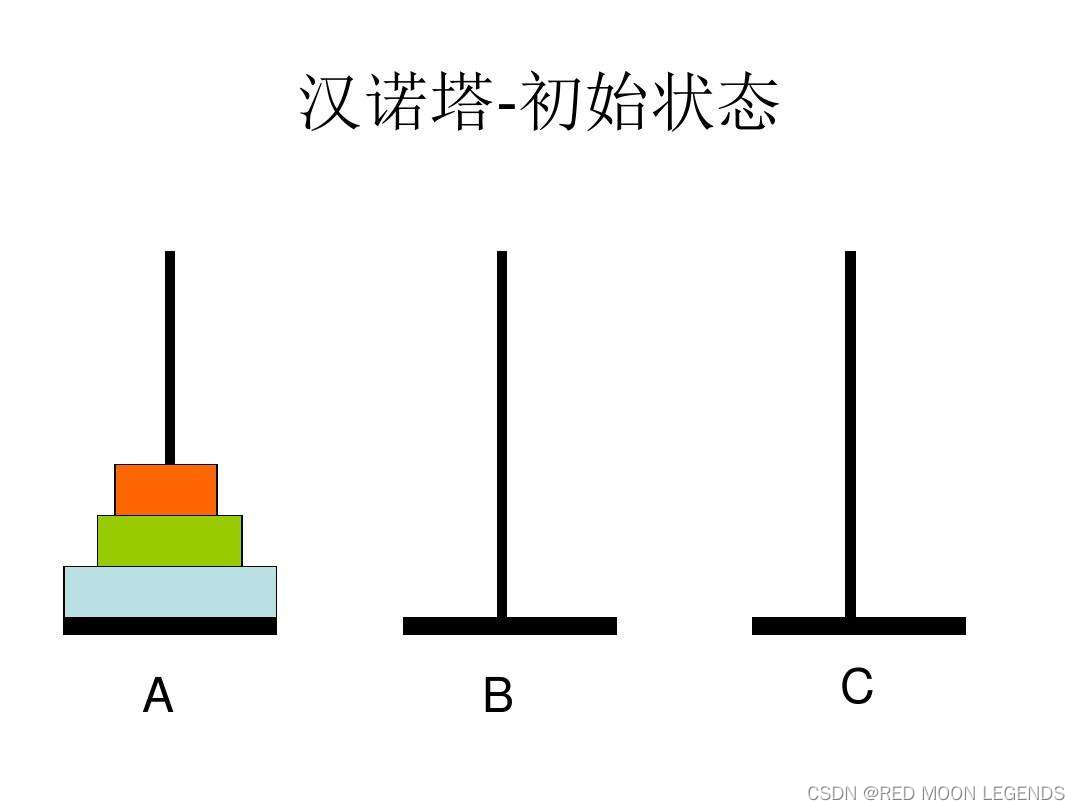

2. 背景

法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

大家听了这个背景故事有没有对汉诺塔产生更大的兴趣呢，毕竟它与世界末日息息相关嘛，但是我们真的等得到那一天吗？

3. 数学思想

其实汉诺塔问题只是一个简单的数学问题，由分析易知：

如果考虑把64片金片，由一根柱子上移到另一根柱子上，并且始终保持上小下大的顺序。这需要多少次移动呢?这里可以先进行枚举，找到对应的数学规律。假设有n片，移动次数是f(n）。则有：

由上述分析可以得到两个函数关系: (1) f(n)=2^n-1 (2) f(n)=2*f(n-1)+1

而由我们之前在C语言中学到的函数递归知识可知，可以将数学函数关系式利用在代码中，形成一个求移动步数的函数递归式。相关代码如下：

这样就可以简单的知道n层汉诺塔问题需要移动的步数了。

所以可知当n=64时，假如每秒钟一次，一个平年365天有31536000秒，闰年366天有31622400秒，平均每年31557600秒，计算得：18446744073709551615秒，大约5900亿年，可能到时太阳系真的毁灭了，但是我能肯定的是我以及各位怕是看不到那天了。

补充：在后面的刷题过程中，我遇到了一种汉诺塔问题的进阶题，就是移动盘子的过程中只能够相邻柱间移动，这里仅仅补充一下这个问题的结论——移动次数f(n)=3^n-1,就不多多介绍了，有兴趣的可以自己去了解下。

重点知识前来张晚霞图，给各位放松放松哈

4. 执行过程的具体分析（重要理解）

(1) 过程简易分析(以三层为例)

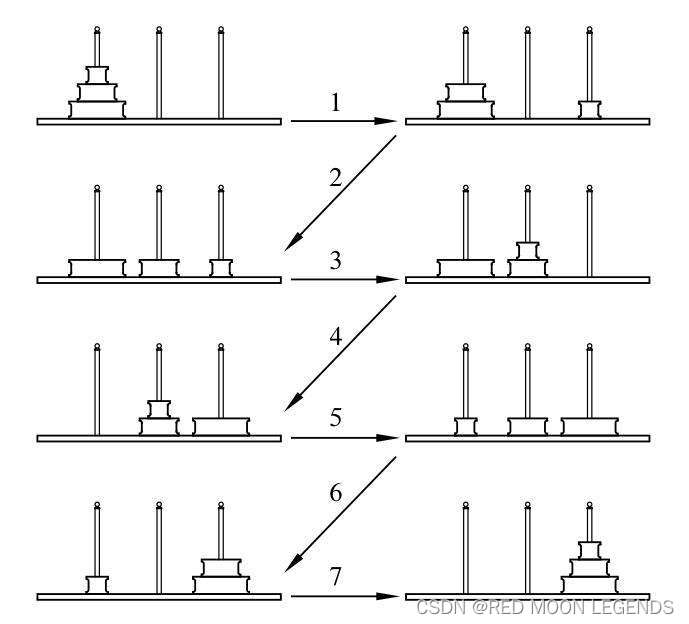
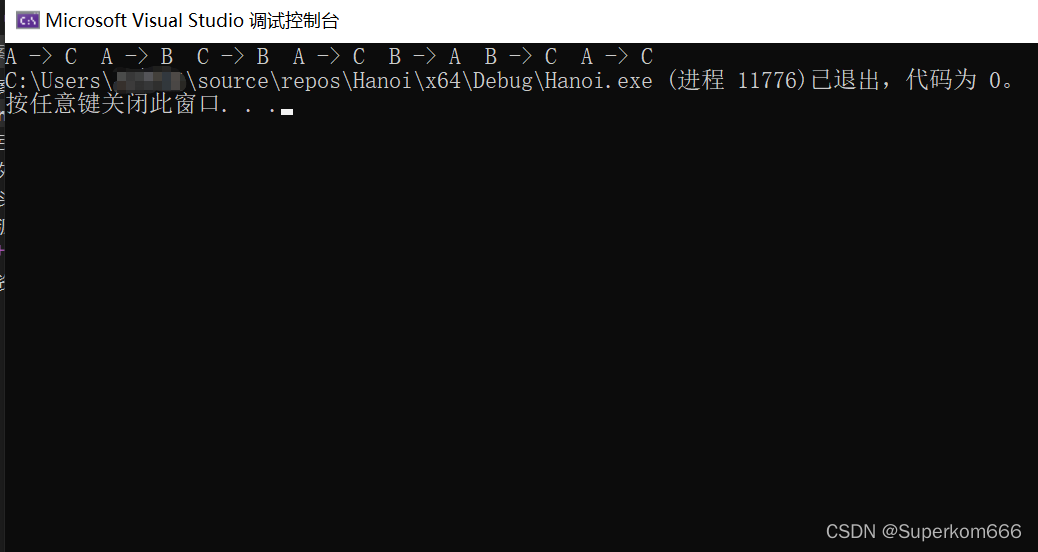
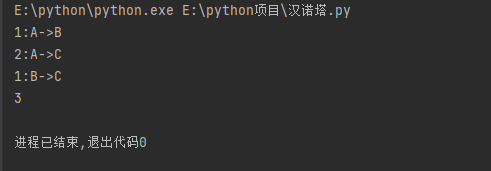
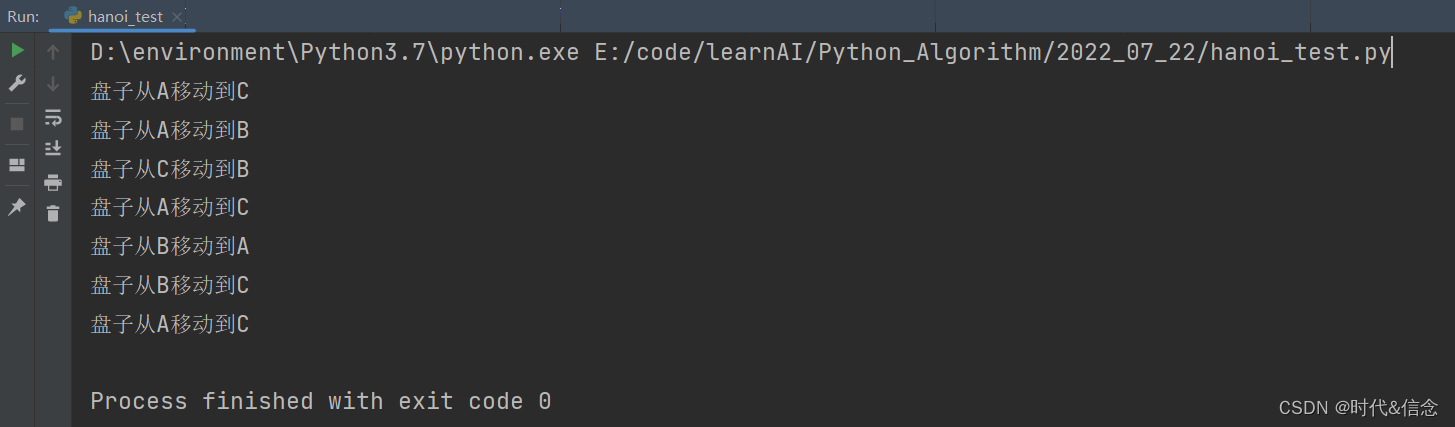
将起始柱命名为‘A’,中转柱命名为‘B’,目的柱命名为‘C’,所以可以得到操作顺序为：

A-->C,A-->B,C-->B,A-->C,B-->A,B-->C,A-->C;共七步。

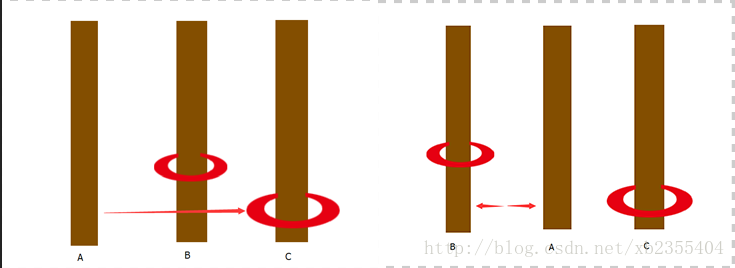
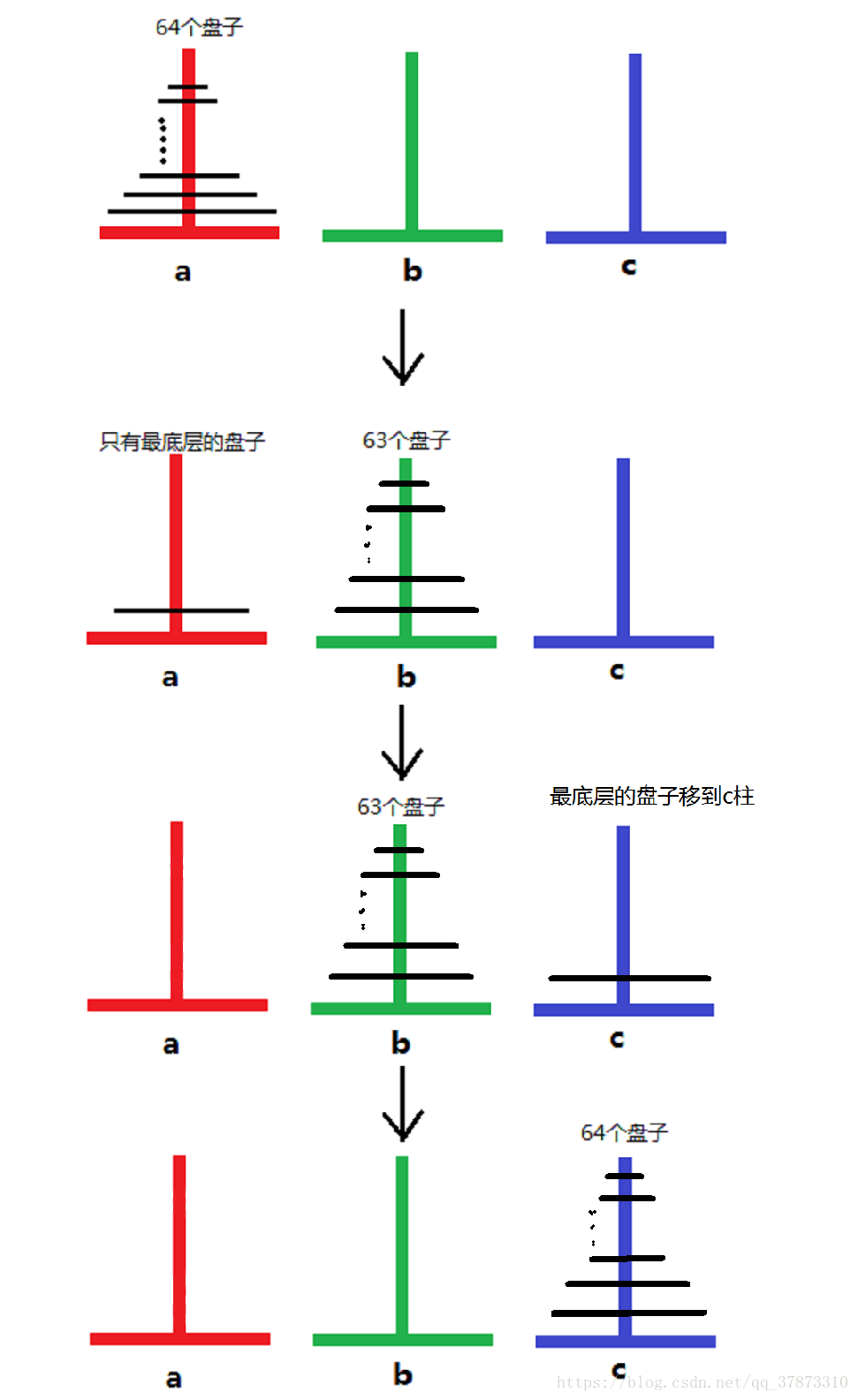
由上述简单分析可以得到汉诺塔问题的三步过程:

一: 将n-1个盘子从A杆经过C杆移到B杆

二: 将A杆上第n个盘子移到C杆上

三: 将B杆上的n-1上盘子经过A杆移到C杆上

这样经过三步后，一个汉诺塔就完成了。

(2) 思考

由上述分析也可以知道这是一个相似且反复的过程，因此由我们以往的经验也可以得出整个过程满足函数递归。而既然是一个函数递归问题，那就有两个问题我们值得思考。

(1) 这个递归的中相似的部分是什么？即要找到函数递归的条件。

(2) 这个递归的出口是什么？即我们要如何做才能趋于这个递归的出口，找到这个递归的终止语句。

解决这两个问题，我们也就能很好的理解汉诺塔问题中的函数递归。

(3) 解答

通过我们对三层汉诺塔的分析，我们可以知道汉诺塔问题的本质，即将A杆中的n个盘子通过B杆全部移到C杆上，这样我们就可以简单的写下这个函数HNtower（n，A，B，C），并且我们可以找到其中的相似部分。

(4) 递归说明

（1）要将A杆上的n-1个盘子通过C杆移到B杆（第一步）

这里就可以与我们定义的汉诺塔函数联系起来，而得出递归的第一层HNtower（n-1，A，C，B）

（2）要将B杆上的n-1个盘子通过A杆移到C杆上（第三步）

这样可以得到递归的第二层HNtower（n-1，B，A，C）

但是，由三层汉诺塔也可以知道在函数递归过程中只有这两步也不够，我们除了找到这两个相似点外，还有一个十分重要的条件，那就是我们还需要在两步递归中定义调用一个移动函数Move(A，C);而由这个函数的两个参数我们也可以知道它的作用:将A杆的盘子移到C杆上(即在执行完第一步后，我们要将A杆上剩余的最大盘移到C杆上)，即

递归出口:

找到这两层递归后，我们已经解决了汉诺塔问题的一半了，但是还有一个很重要的，也就是

这个递归的出口。而要找到这个出口，其实也不难，我们可以想一想，一个程序的出口是什么呢？无非就是这个程序的最后一步，而汉诺塔的最后一步可以简化为一层汉诺塔问题（即将1个盘子从A杆直接移到C杆上）,这样我们也就找到了这个递归的出口,也就是（n＜=1）。

但是我们又要怎样趋于这个出口呢？其实这个问题我们早就解决了，递归中的第一个参数(n-1)在递归多次进行之下不就会趋于这个出口，所以我们在思考递归函数的参数时十分重要，这就要我们多多练习与函数递归有关的习题来培养一种思维能力(小编的思维能力也很差，我们一起加油)。

由上述分析，我们就可以得到这个汉诺塔函数的相关代码

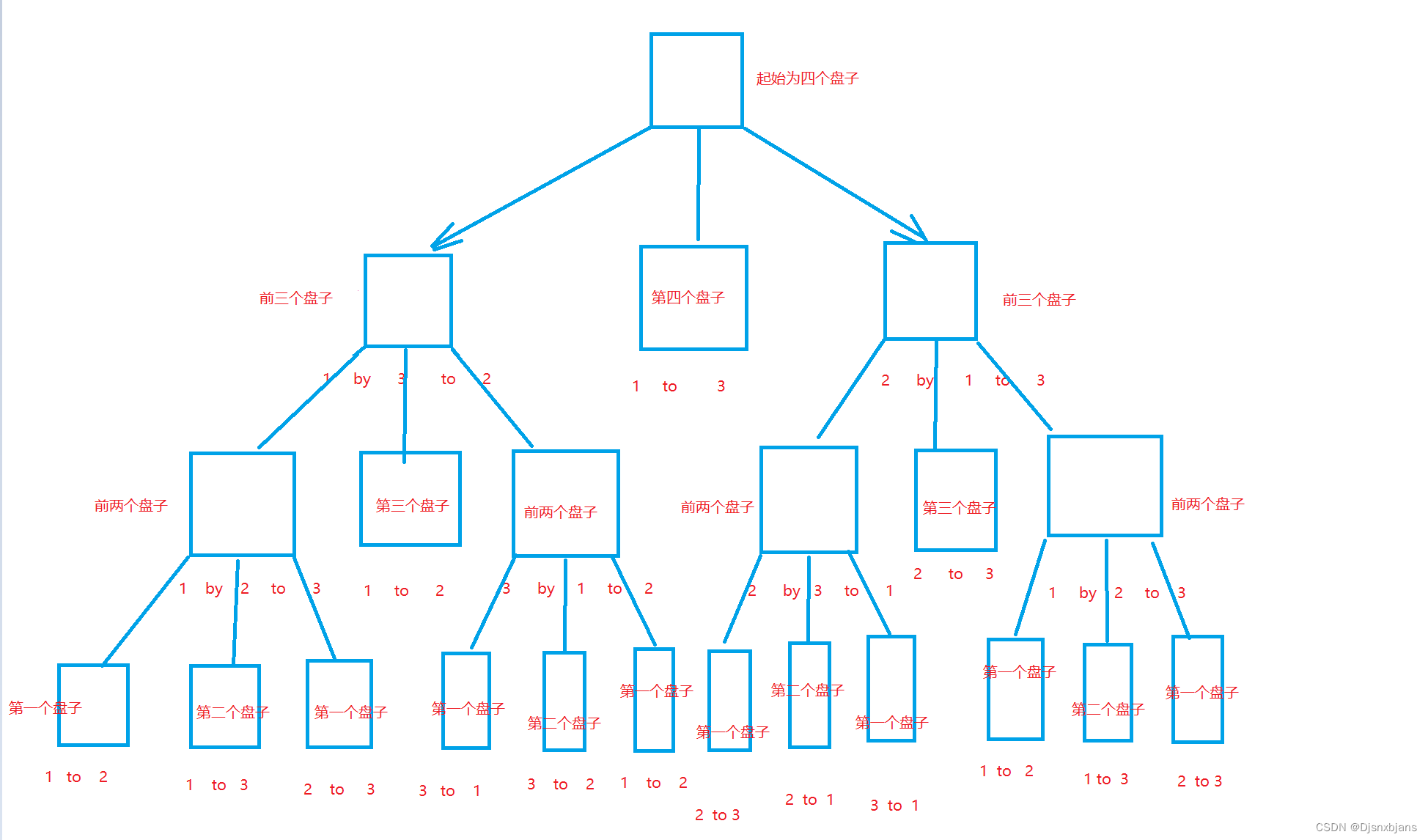
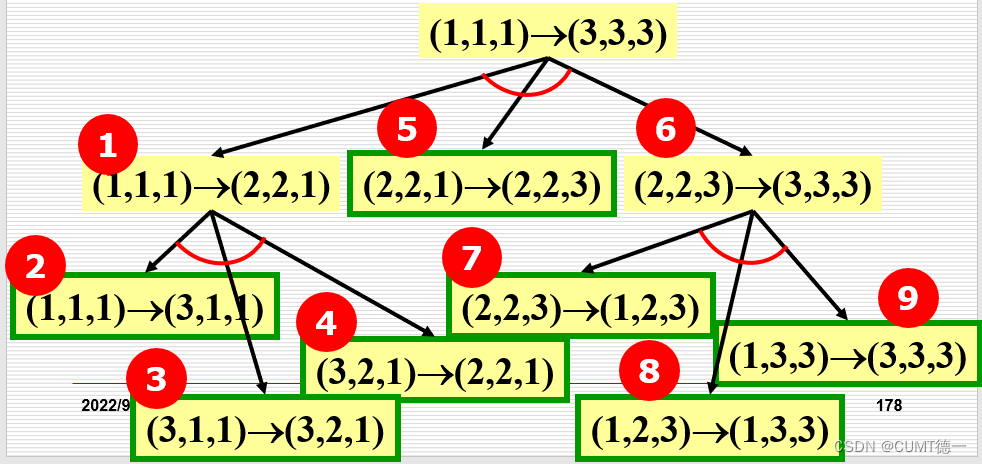
图示分析递归实现的过程:

注:图是在纸上画的，我已经尽量保证清晰度以及完整的过程了，希望大家能认真分析一下，如果觉得不方便看，我建议可以抄写一份在自己的纸上慢慢分析。(图上的小记号要注意哈)

提醒一下哈，下三张图表示了三层汉诺塔的六次传参以及五次递归，其中的大写数字(一，二，三等等)是各个传参过程具体分析，而不同张纸上相同数字表示的是同一个函数(主要是我觉得要把相关性强的部分放在一起，导致了一些重复函数在不同的纸上，大家要分清楚)。

为了各位能更好的理解，我会将图示简要分析一下。

细品:

我在图中汉诺塔函数的各个参数上标明了一些小写字母(x,y,z)作为识别标志。将起始过程的A柱标记为x，B柱标记为y，C柱标记为z，我们可以将传参过程中参数的变化转换成标记字母的变化以便观察。
汉诺塔问题的递归分析其实并不难，主要是我们要区分与函数参数以及函数在传参过程中对应参数分别表示什么。(即图中x,y,z在传参过程的变化)

在此我要说明一下:在函数内部调用参数时，是对应字符对应相关参数，而函数传递参数时，则是对应参数位置对应相关参数。

再次强调图中x,y,z是我为了分析而规定的，实际并不存在，真正过程对应的还是柱子的标号(A，B，C)，希望各位好好区分，好好理解一下。

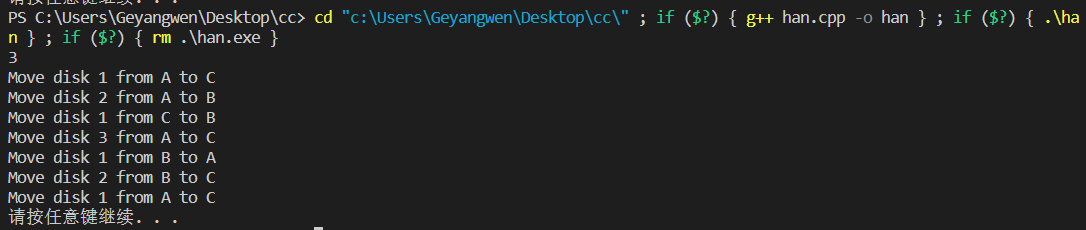
5. 整体代码及显示效果

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
void Move(char x, char y)
{printf("%c --> %c\n", x, y);
}
void HNtower(int a, char A, char B, char C)//汉诺塔函数实施主体,A为初始柱,B为经由柱,C为目的柱
{if (a == 1){Move(A, C);}else{HNtower(a - 1, A, C, B);//第一个递归式Move(A, C);HNtower(a - 1, B, A, C);//第二个递归式}
}
int MoveNum(int a)
{if (a == 1)return 1;elsereturn 2 * MoveNum(a - 1) + 1;//为了对应递归主题，用递归式表示
}
int main()
{int a = 0;printf("请输入你选择的层数:>");scanf("%d", &a);int Num = MoveNum(a);printf("%d层需要移动%d步\n", a, Num);printf("具体过程如下\n");HNtower(a, 'A', 'B', 'C');//进入递归函数return 0;
}