一.汉诺塔问题及其递归算法
1.问题阐述
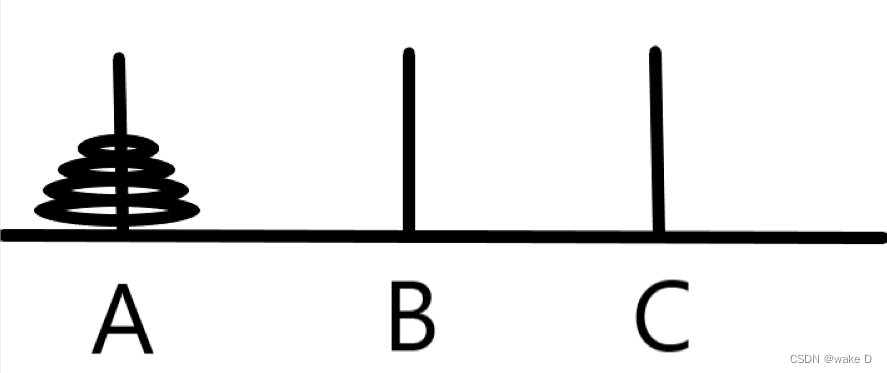
经典汉诺塔:

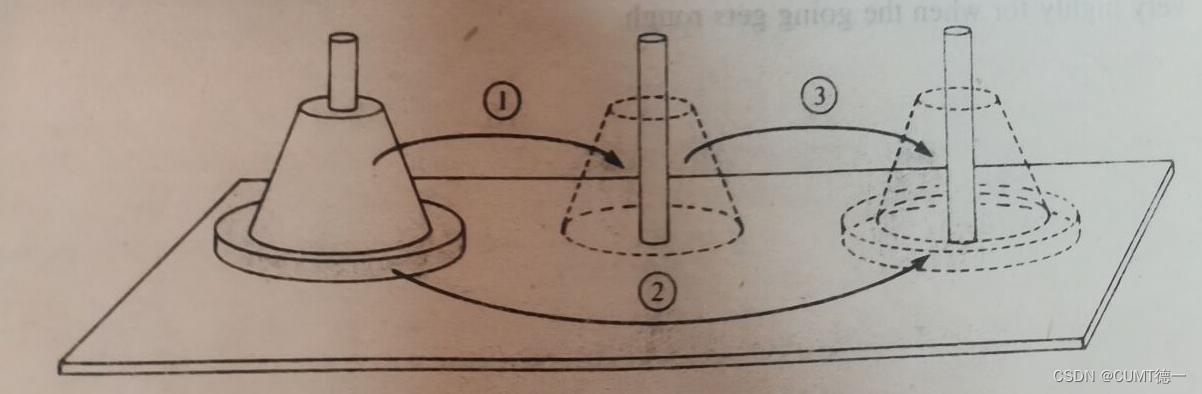
外文算法书对汉诺塔问题的描述:
2.算法步骤
三阶汉诺塔问题解题步骤
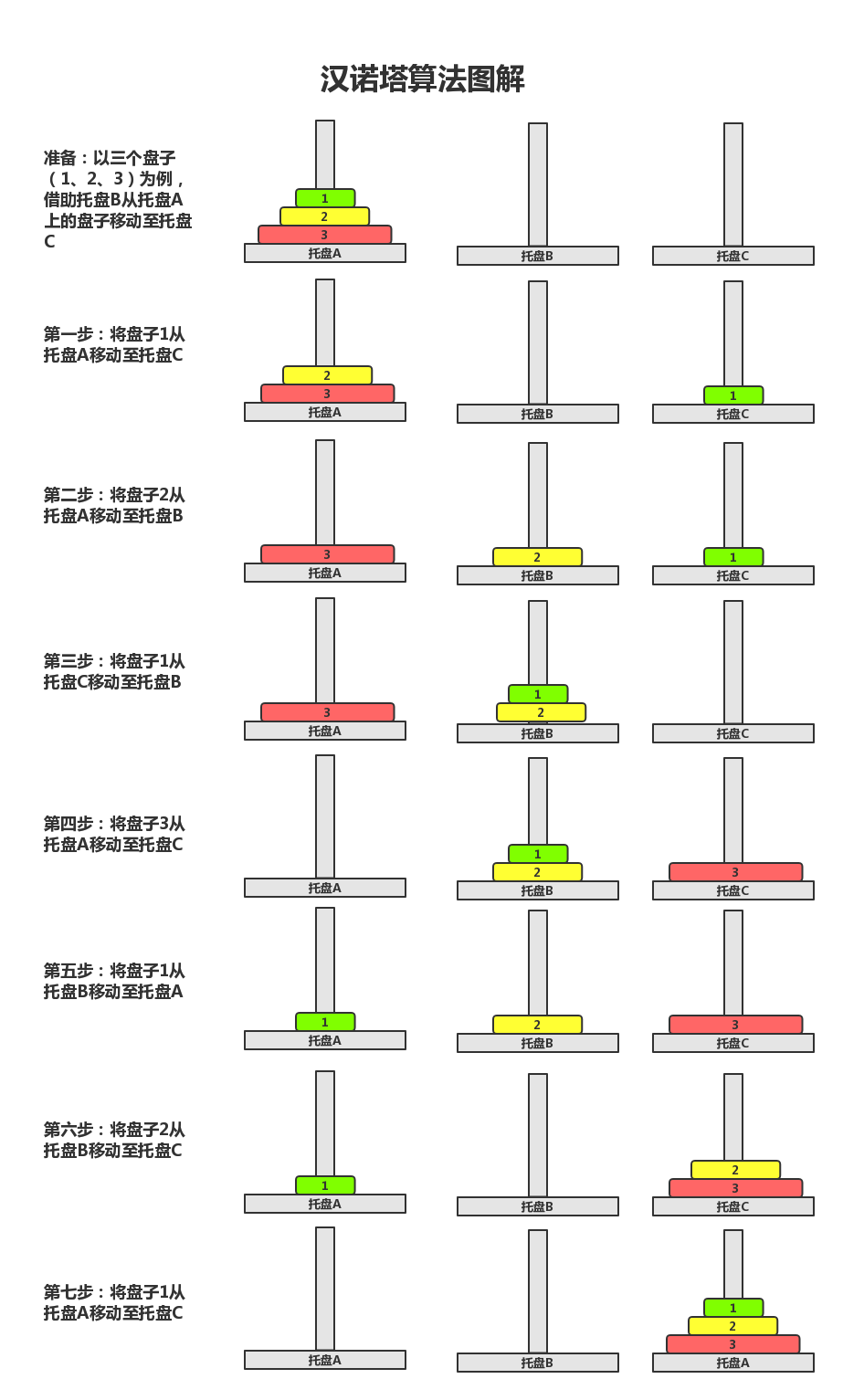
共需7步。
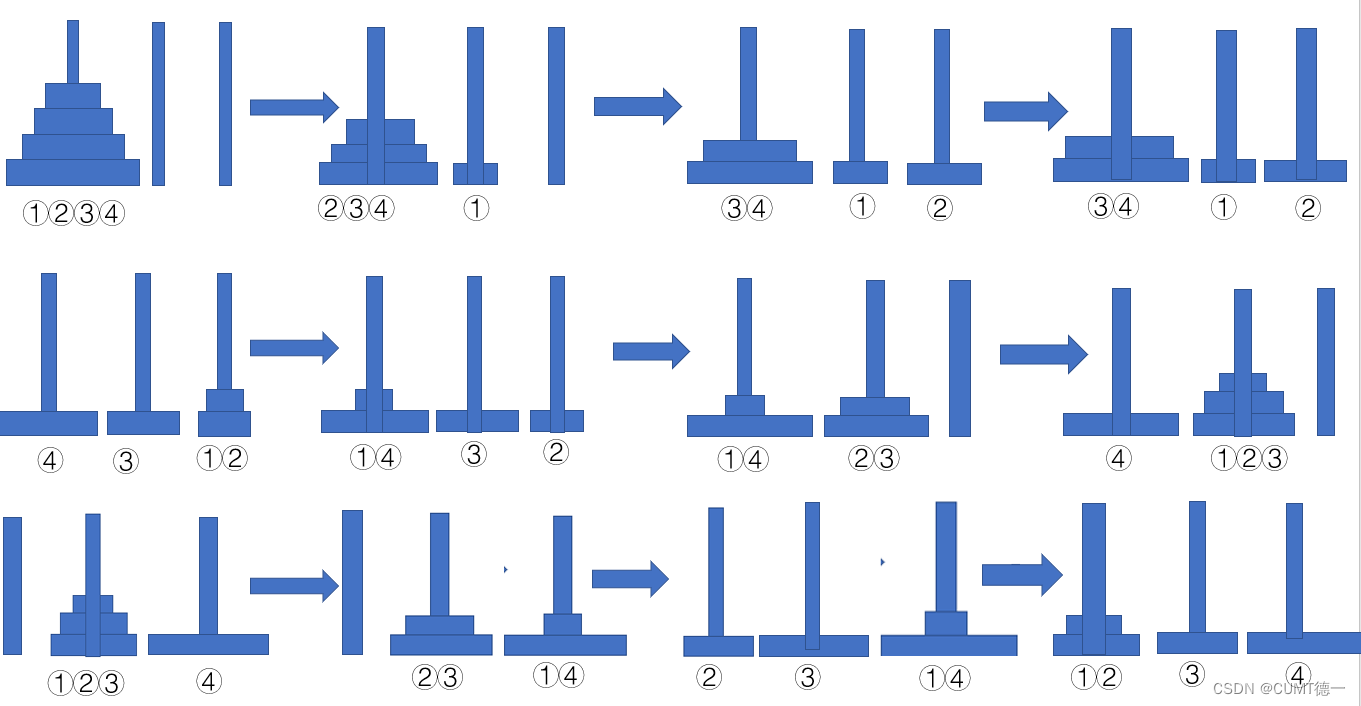
四阶汉诺塔问题解题步骤

共需15步
五阶汉诺塔问题解题步骤
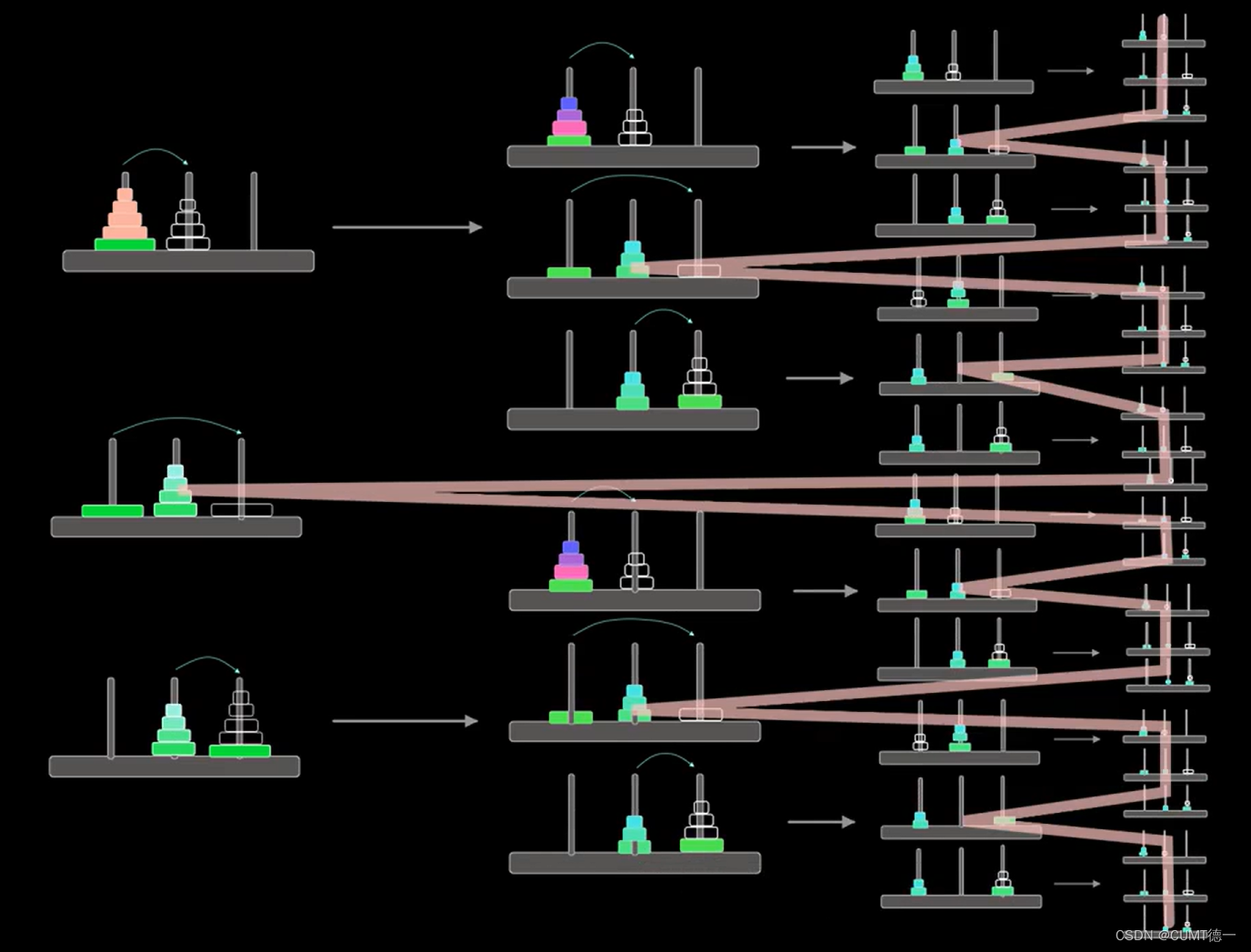
算法采用了分治的思想,利用递归的方式,完成n层汉诺塔的移动。
问题解法:
当n=1时,只要将编号为1的圆盘从柱子A直接移到柱子C上即可。
当n>1时,就需要借助另外一根柱子来移动。将n个圆盘由A移到C上可以分解为以下几个步骤:
(1) 将A柱子上的n-1个圆盘借助C柱子移到B柱子上;
(2) 把A柱子上剩下的一个圆盘从A柱子移到C柱子上;
(3) 最后将剩下的n-1个圆盘借助A柱子从B柱子移到C柱子上。
假定n是圆盘的数量,T(n)是移动n个圆盘的移动次数。
当n=1时,T(1)=1
当n=2时,T(2)=2T(1)+1
当n=3时,T(3)=2T(2)+1
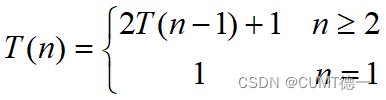
- 递归关系式:
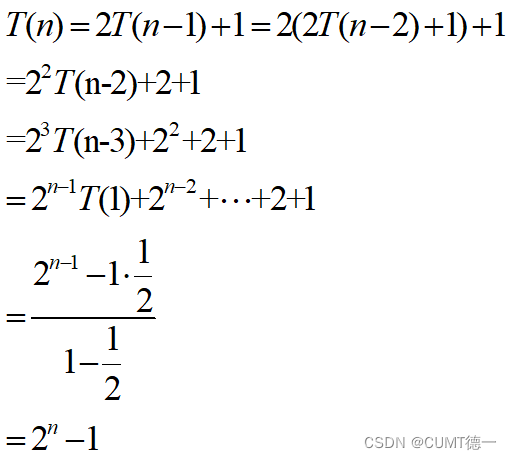
所以,n阶汉诺塔问题最少共需要2的n次方减1步
算法的时间复杂度为
![]()
3.代码表示:
void Hanoi(int numberOfDisks, char start, char destination ,char spare)
{//只有一个盘子时,从起始桩移到目标桩if (numberOfDisks == 1) {cout << "move the disk from peg 'start' to peg 'destination'<<endl; }//超过一个盘子时else if(numberOfDisks > 1){Hanoi(numberOfDisks-1, start , spare , destination); //将n-1个盘子移到过渡桩cout << "move top disk from peg 'start' to peg 'destination' << endl; //将剩下的一个大盘移到目标桩Hanoi(numberOfDisks-1, start , destination , spare); //将过渡桩的n-1个移到目标桩}
}二.汉诺塔问题的非递归算法
汉诺塔问题也可以借助非递归算法来解决,有许多种非递归算法可以解决汉诺塔问题,博主认为最常见的是利用递归二叉树,下面列举两种非递归算法。
1.利用二叉递归树
文献[4]指出:汉诺塔问题的递归算法代码与二叉树的中序遍历算法代码十分相似,故采用了二叉树的中序遍历,发现汉诺塔问题的算法步骤正好可以画成一棵完全二叉树,其中序遍历过程就是汉诺塔问题的算法步骤。
函数move(N-1,s,e,t) N:盘子数 ,s:起始桩 e:目标桩 t:过渡桩
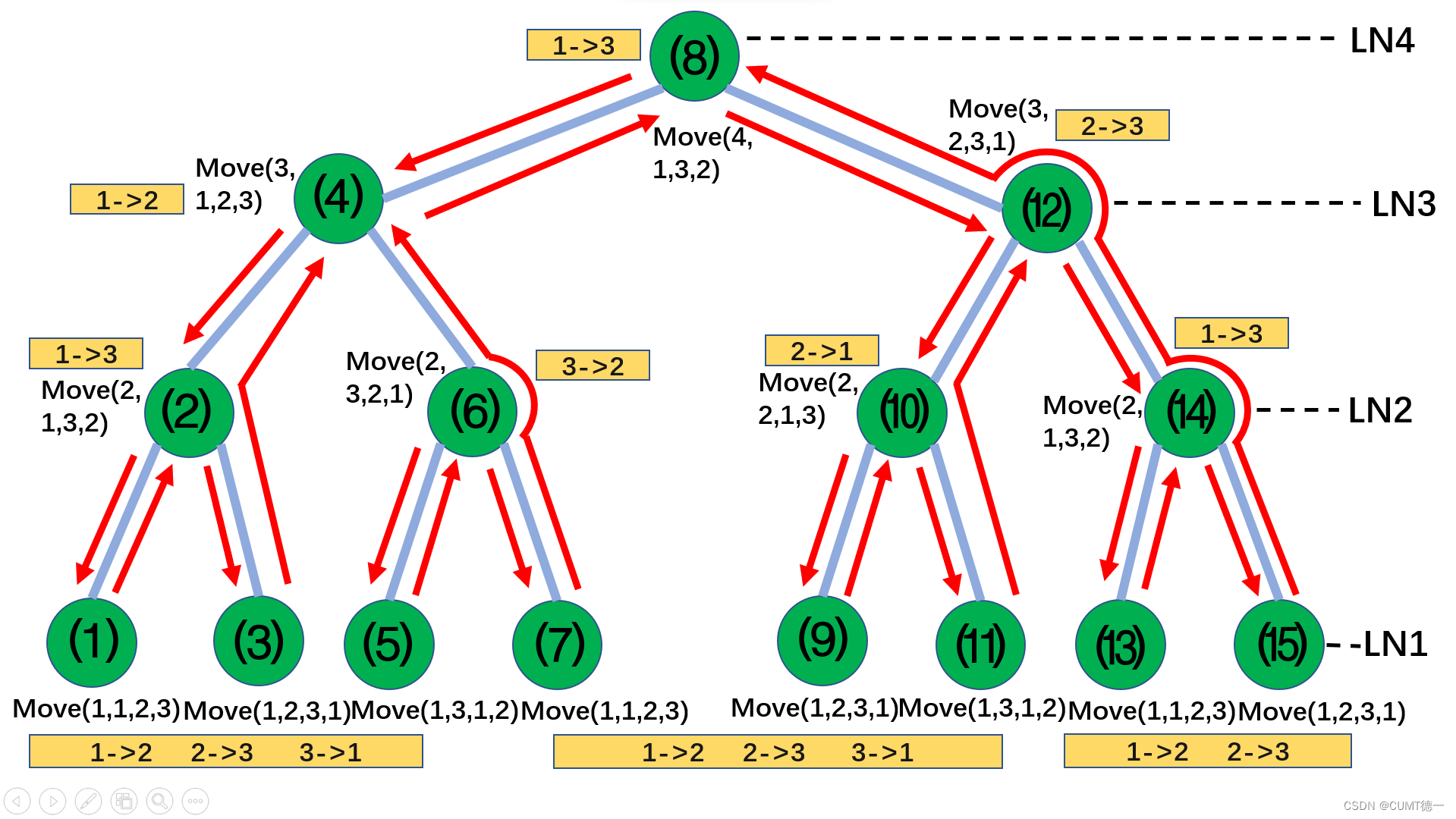
完全二叉树结点个数正好是2^n-1,与汉诺塔最优解法的步骤数相同
结点1到结点15正好对应4阶汉诺塔问题的15步
要解决的问题:
(1)第i步(即结点i)应移动哪一盘片?
由图可知,同一层总是处理同一盘片,
第LN层各结点编号的最大公约数为2^(LN-1)
所以,求出第i步对应的LN,就能求出应该移动哪一盘片
文献[4]给出的方法是:
LN=1 ,j=2;
cin>>i;
while(i%j==0)
{j*=2;LN++;
}例如i=12,12%2=0,所以j=4,LN=2;
12%4=0,所以j=8,LN=3;
12%8!=0,所以LN=3,结点i在第三层知道第i步应该移动谁之后,还要知道从哪移到哪
(2)如何确定每一步盘片移动的起止桩编号?
- 规律1:各层从左到右的第一个结点移动盘片时,起始桩编号都是1,目标是2或3(请看1,2,4,8四个结点);
- 规律2:树的总层数N与结点i所在层数LN同奇或同偶时,目的桩为3,否则为2;
- 规律3:由图可知,树的每一层内都有固定回路,有的是“1->3,3->2,2->1",有的是“1->2,2->3,3->1"。周期都为3。
那么只需要知道 :
1.所在层起始结点是哪种模式?(1->2还是1->3)
2.i在所在层的横向编号?(i是所在层从左到右的第几个结点)
3.i结点在循环回路中的第几个位置?(1/2/3)
-
问题1:所在层起始结点是哪种模式?(1->2还是1->3)
设结点i所在层的起始结点的起止桩编号为(s,d)
由规律1、2,s=1,d=3-(N-LN)%2,假设i=11,则LN=1,d由前面公式算出等于2,
所以,i所在层最左侧结点开始为"1->2",则该层的循环回路为:“1->2,2->3,3->1"
-
问题2:i是所在层从左到右的第几个结点?
设是第Sn个,Sn=Round(i/2LN)(Round为四舍五入),例如i=11,则LN =1,Sn由前面公式得出为6,那么i在第1层从左往右的第6个结点。
-
问题3:i结点在循环回路中的第几个位置?
设在第p(1<=p<=3)个位置,p=(Sn-1)%3+1,例如i=11,则LN =1,Sn=6,p由前面公式算出等于3,所以结点i在“1->2,2->3,3->1"循环的第三步,也就是“3->1"。
所以,如果问:汉诺塔问题的走法中,第i步应该移动谁?怎么移动?
根据上面公式,求出LN,d,Sn,p的值,就可以做回答
2.利用逆序编码
文献[5]采用了逆序编码的方式
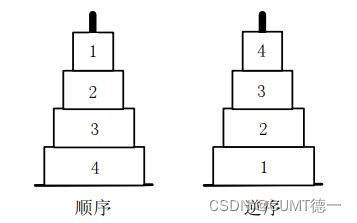
3阶汉诺塔搬移:

4阶汉诺塔搬移:

去除4号盘的4层汉诺塔搬移顺序:

发现4层汉诺塔搬移中,去掉4号盘之后,剩下的搬移路径与3阶汉诺塔完全相同
得出结论:
完成 n 层汉诺塔的搬运,前 1,2,…,n-1 号圆盘的搬运次数、顺序与完成 n-1 层汉诺塔的搬运 相同。(只有在逆序编码时成立)
其他定理与算法代码可以去文献[5]中阅读。
三.双色汉诺塔

采用数学归纳法:
设f(n)为双色汉诺塔的移动规则,g(n)为普通汉诺塔的移动规则,n为圆盘个数。
很容易知:
f(1) = g(1);
f(2) = g(2);
f(3) = g(3);
假设 f(k) = g(k) , f(k+1)=g(k+1) 若能证明f(k+2)=g(k+2),则结论得证
证明:

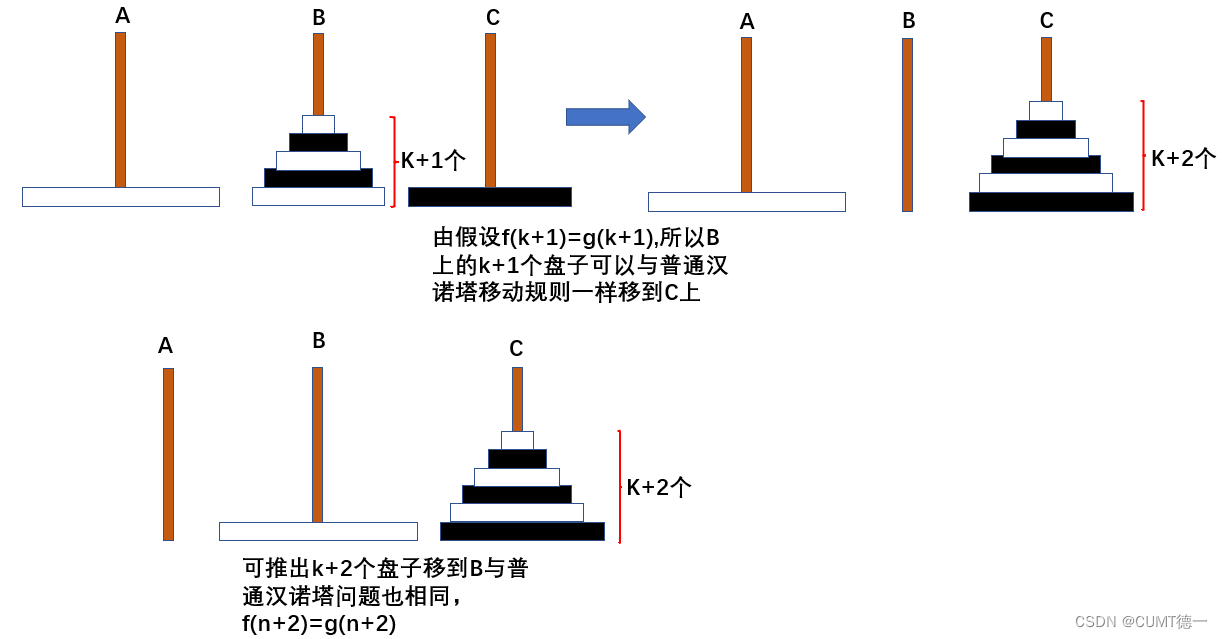
所以可得出结论,双色汉诺塔问题与普通汉诺塔问题相同
四.利用启发式算法解决汉诺塔问题
1.A算法处理汉诺塔
f(n)=g(n)+h(n)
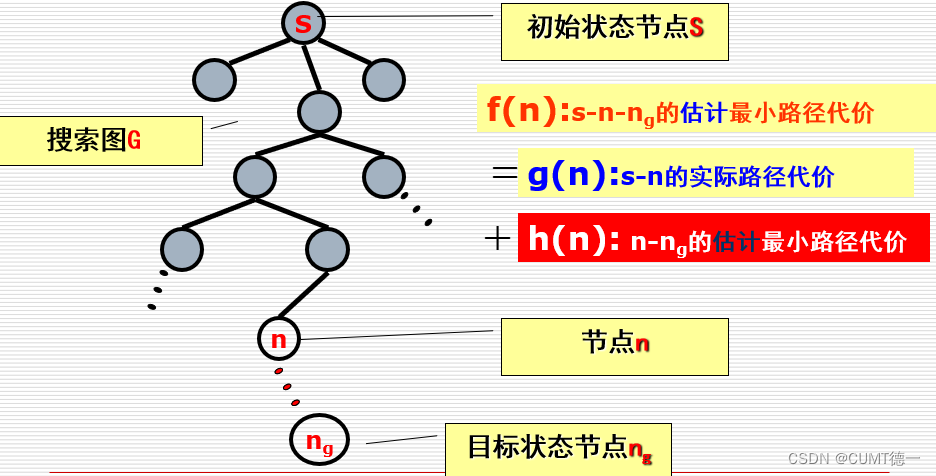
关键在于估计函数h(n)的设计
一种设计方案是文献[7],
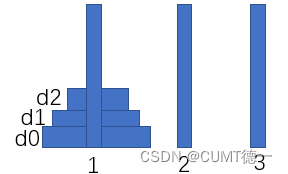
设起始状态空间是I=<1,1,1>,目标状态空间是G=<3,3,3>,移动函数move(di,destination)。
设g=G0+G1+G2,评价函数设计为:f(x)=g(x)+h(x),h(x)=| g - (d0+d1+d2) |

发现此种方案只能保证找到解路径
文献[8]给出了另一种方案:
应用极值方法,考虑极端的情况,确定其上限和下限,把考虑对象限制在每个托盘中的最顶上的两个盘子。如果托盘中只有一个盘子,也没有关系,另一个盘子作为 0 处理;如果托盘中一个盘子都没有,那么最顶上的两个盘子都做 0 处理,这样不会影响结果。然后比较托盘 中最顶上两个盘子的权值的和,从而决定移动的方向。其移动的方向是:最小的权值之和的托盘移向具有较大的权值之和的托盘。
制定出以下几条规则:
- 规则1:if(a0) if(A.top==1&&B.top==1) { move(B,C); move(A,C);}
else { if(!move(A,B)) move(A,C);}
- 规则2:if(a==0&&b<c) if(!move(C,A)) move(B,A);
- 规则3:if((a==b)>c&&c!=0) if(!move(C,B)) move(C,A);
- 规则4:if(a>b&&b==c) if(!move(C,B)) move(B,C)
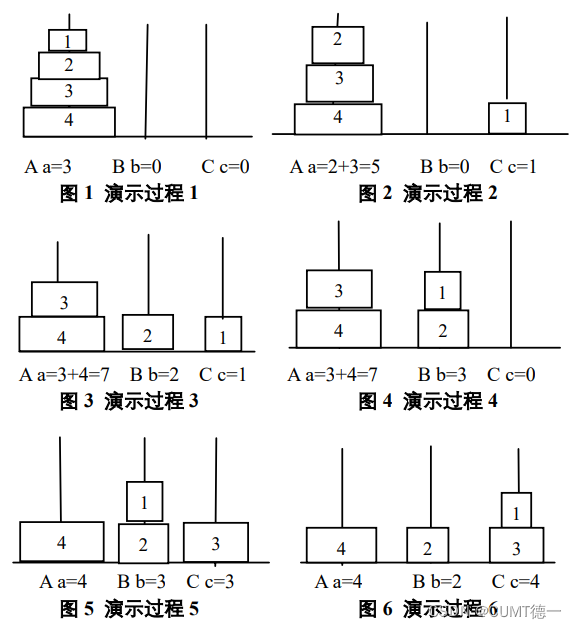
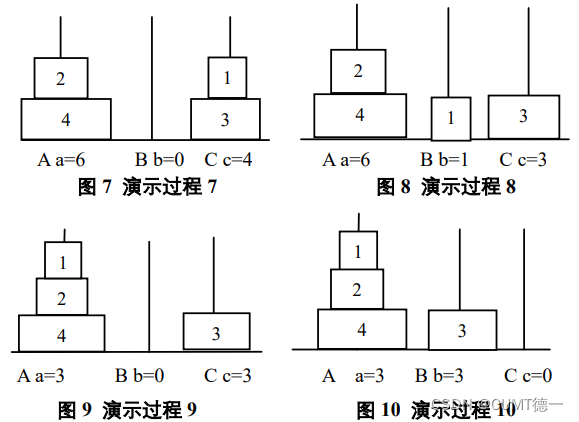
如上图,过程1运用了规则2,过程2运用了规则2,过程3运用了规则1,过程4运用了规则2,过程5运用了规则4,过程6运用了规则3,过程7运用了规则2,过程8运用了规则1,过程9运用了规则2,过程10运用了规则2。
2.利用问题规约法
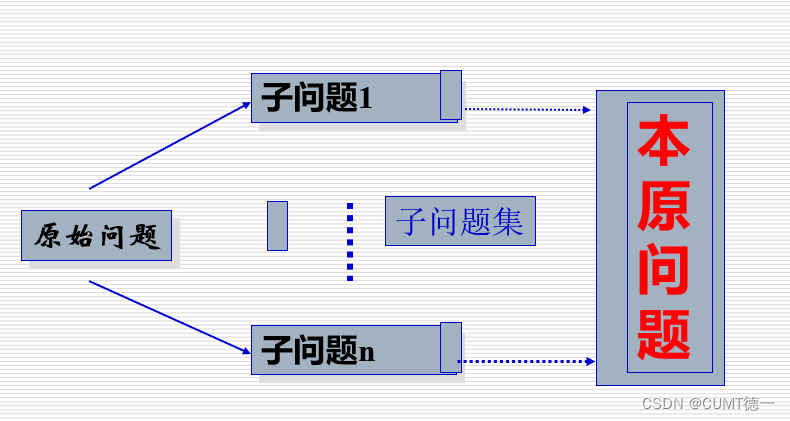
方法与分治类似
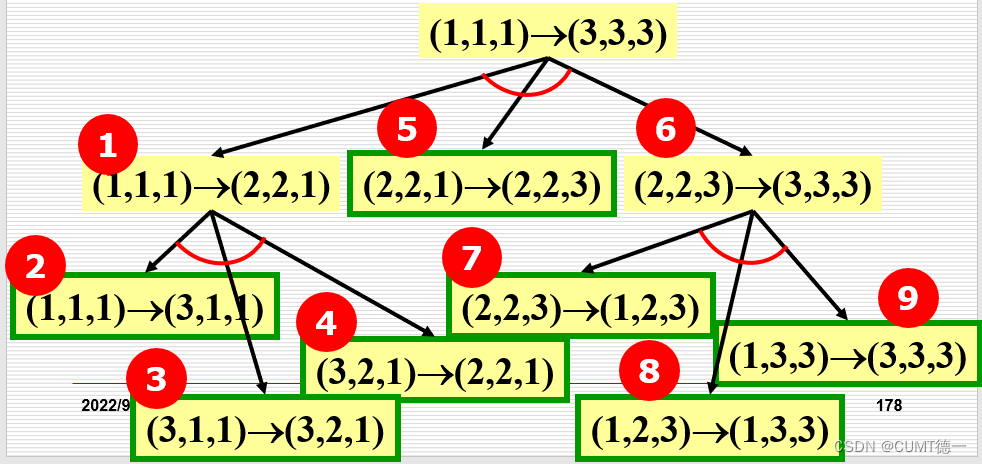
画出每一步的状态空间图,图中的弧线代表逻辑或关系
参考文献:
文献[1] Ames W F . Computer Algorithms — Introduction to design and analysis (second edition)[J]. Mathematics and Computers in Simulation, 1990, 31(6):602-602.
文献[2] 手撕“汉诺塔算法”之详细图解_灰小猿的博客-CSDN博客_汉诺塔算法
三阶汉诺塔问题算法步骤图来自文献[2]
文献[3] b站视频 【汉诺塔小游戏和递归思想】 https://www.bilibili.com/video/BV1Zh411y7XB?share_source=copy_web&vd_source=fa7199f346f857b079aeb8f19090512c (5阶汉诺塔问题图像来源)
文献[4] 彭伟.汉诺塔问题的非递归算法设计及可视化实现[J].武汉船舶职业技术学院学报,2011,10(06):55-59+72.
文献[5] 严海兵.基于逆序编码的汉诺塔非递归算法[J].苏州科技大学学报(自然科学版),2022,39(01):71-76.
文献[6] 王晓东. 计算机算法设计与分析-第 3 版[M]. 北京: 电子工业 出版社,2009.
文献[7] [AI]A*搜索练习题——3传教士3食人族、单臂机器人、汉诺塔_是土豆大叔啊!的博客-CSDN博客
文献[8] 陈炼,邓少波,万芳.A算法在梵塔问题中的应用[J].计算机工程,2005(08):168-170.