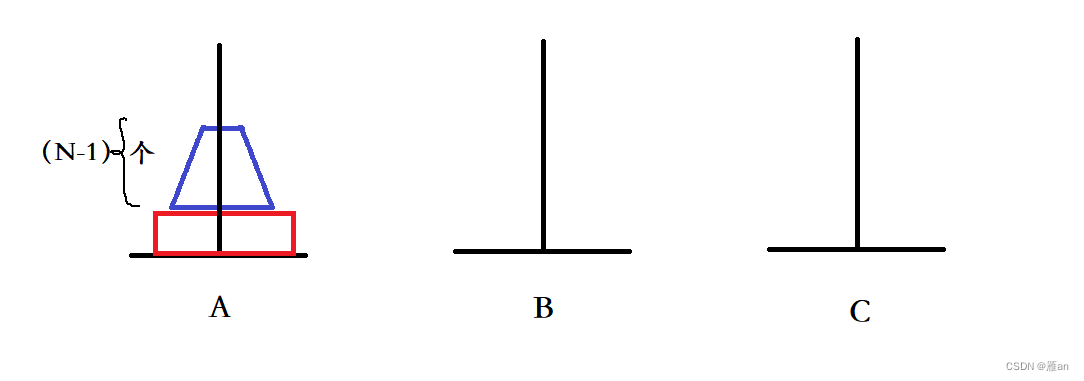汉诺塔问题是一个递归的经典范例。
让我们先从移动一个盘开始,逐渐增加需要移动的盘数。
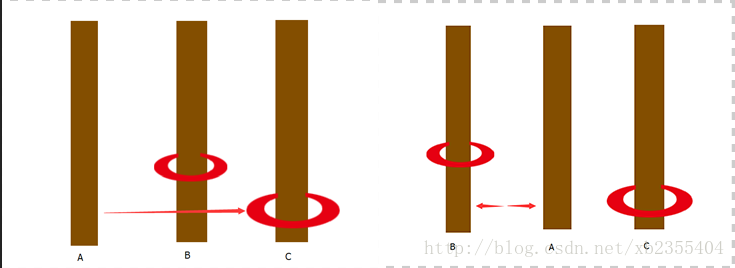
当我们需要移动一个盘时,只需将该盘移动至C杆。
int c = 0;
void move(char a, char b)
{printf("第%d步为:%c->%c\n",++c, a, b);
}
当我们需要移动两个盘时,便需要在移动一个盘的基础上,再移动一个(此时这2个盘最终会移动到B杆,这个问题我们会在后面解决)。
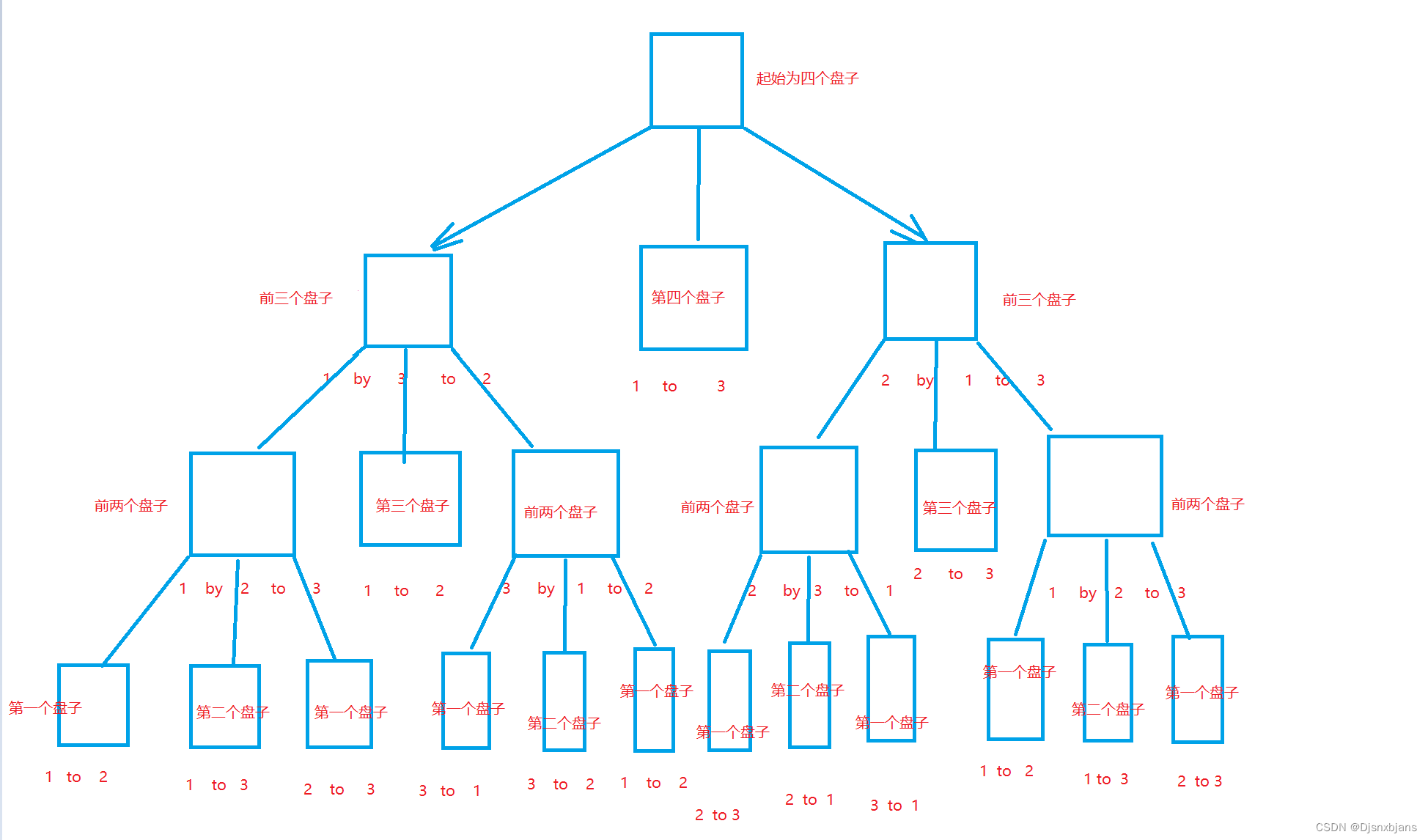
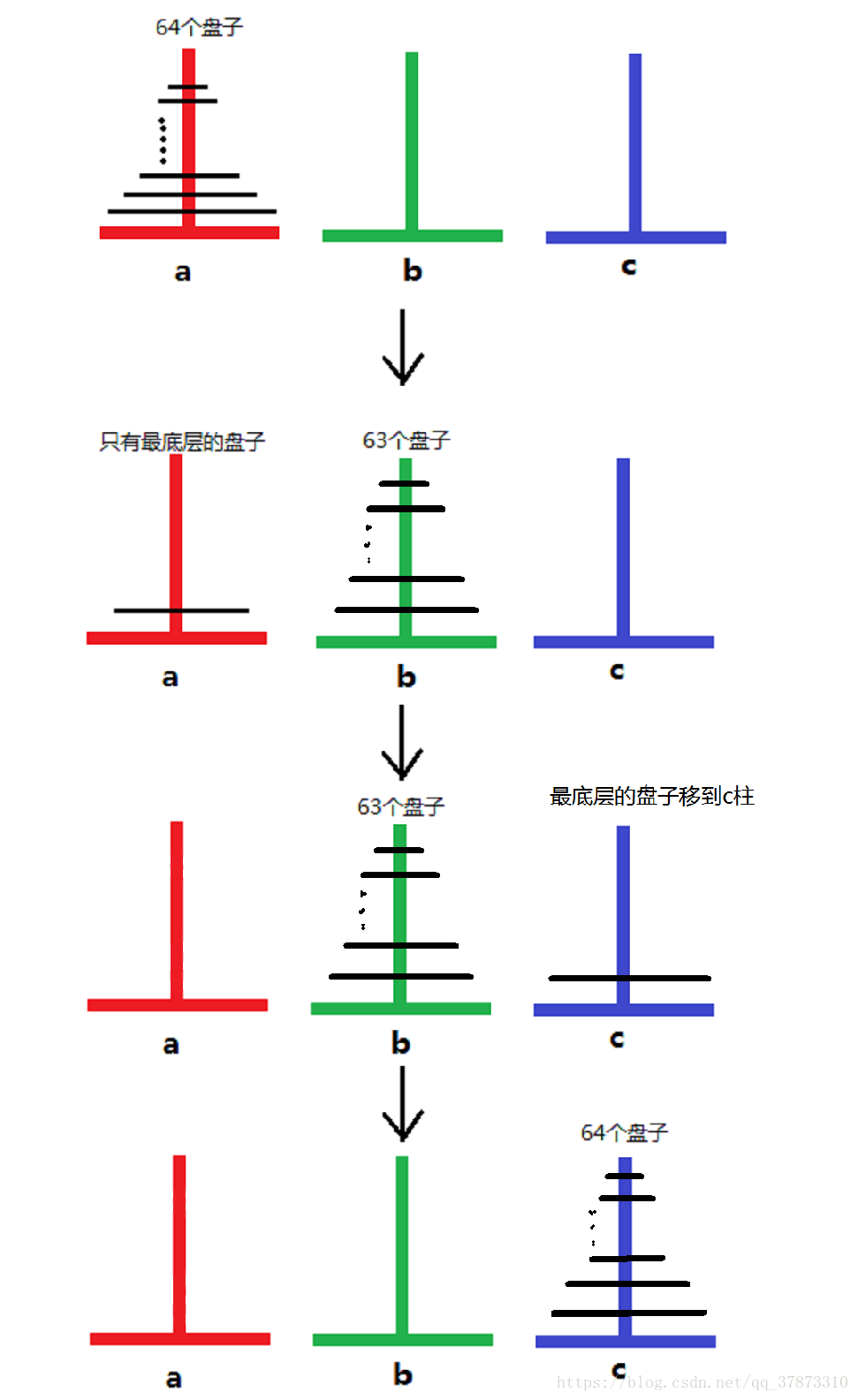
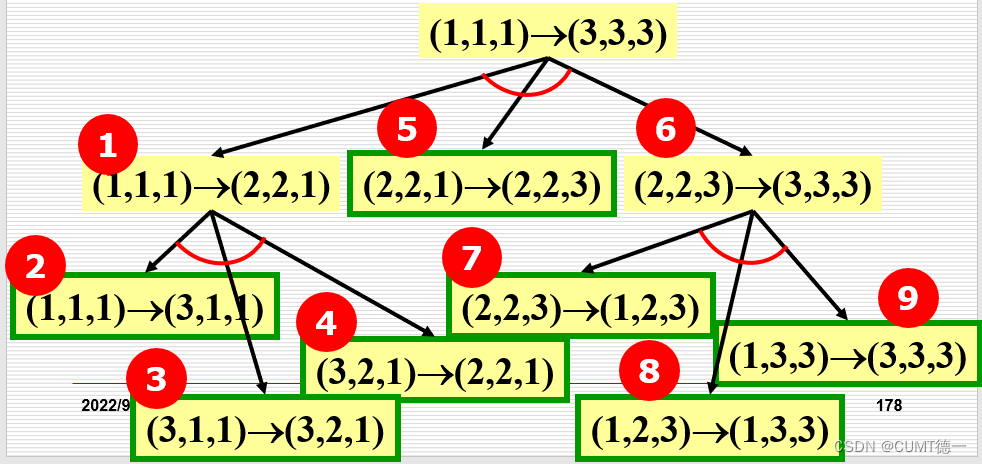
移动三个盘时,便要在移动两个盘的基础上再移动一个,继续增加下去,我们会发现:我们在需要移动n个盘时,只要在(n-1)个盘的基础上再移动一个盘。我们将这n个盘看成两部分,第n个盘,和前(n-1)个盘的整体。这样当n>=2时,都是同样的模型:先将上面的盘移动到B杆,再将最下面的盘移动到C杆,最后将B杆上的盘移到C杆,放在最下面的盘之上。

我们在需要移动n个盘时,已经成功移动了(n-1)个盘,我们只需将移动(n-1)个盘的过程写成一个函数。移动n个盘需要调用移动(n-1)个盘的函数,移动(n-1)个盘需要调用移动(n-2)个盘的函数......最终递推到移动2个盘会调用移动1个盘的函数,这便是函数的递归。
通过以上的思考逻辑,我们会发现:编写递归函数时,虽然程序是在最外层的函数层层调用至最内层,但我们的逻辑出发点还是要落在最内层的函数,也就是递归停止的那层函数。
但是当我们尝试写出代码时,会发现出现了新的问题,那就是我们调用的移动(n-1)函数最终会将(n-1)个盘移动到C盘,这也就代表着第n个盘只能移动到B杆,所以最终这全部n个盘也会在B杆。探寻一下规律,我们会发现,移动到B杆和移动到C杆的现象是交替出现的。我们当然也可以通过单双数来区分,但这样不仅麻烦,而且低效。因为在代码中,杆不是实体,只能用符号储存在变量中来表示对应的杆。我们尝试将杆的位置看成储存杆的变量,而杆本身只是一个符号

我们在调用移动(n-1)的函数时,可以通过函数的形参进行“换杆”。我们只需要在调用函数时更换参数位置,便可以将形参中的值互换,实现“换杆”操作,保证无论移动多少个盘,最终都在C杆上。
void hanotower(int n, char a, char b, char c);hanotower(n - 1, a, c, b);//将(n-1)个盘整体移动,并将c杆与b杆交换位置
最后一步便是将b杆的(n-1)个盘整体移到C杆,放在第n个盘之上。相信在接受了以上的思想后,这一步也会自然的以这个思路思考。既然能将A杆到C杆修改为A杆到B杆,自然也能将其修改为B杆到C杆。依然只需要在调用函数时改变参数位置。
void hanotower(int n, char a, char b, char c);hanotower(n - 1, b, a, c);//将(n-1)个盘整体移动,并将a杆与b杆交换位置全部代码为:
#include<stdio.h>
int c = 0;
void move(char a, char b)
{printf("第%d步为:%c->%c\n",++c, a, b);
}
void hanotower(int n, char a, char b, char c)
{if (n == 1)move(a, c);else{hanotower(n - 1, a, c, b);//将(n-1)个盘整体移动,并将c杆与b杆交换位置move(a, c);hanotower(n - 1, b, a, c);//将(n-1)个盘整体移动,并将a杆与b杆交换位置}
}
int main()
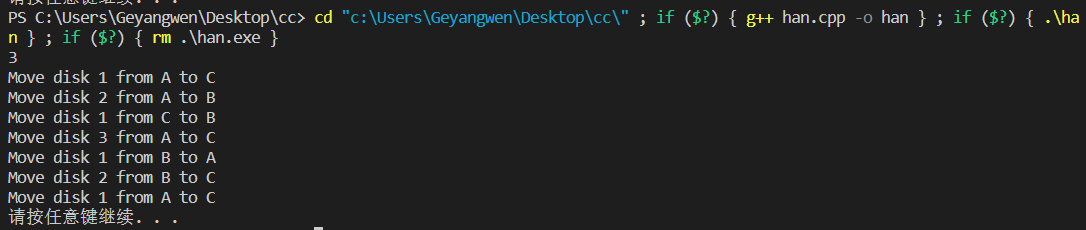
{int n = 0;scanf_s("%d", &n);hanotower(n, 'A', 'B', 'C');return 0;
}通过这个例子,我们可以初步理解一些递归的思想,也能把握一些理解递归的方法:
1.由里到外,从递归终止的那层开始,理解每一层函数的作用
2.在使用时,知道每一层函数的作用就已经足够了,在编写时试图由外向内将代码一层层展开来理解反而容易感到困惑,影响使用的逻辑。