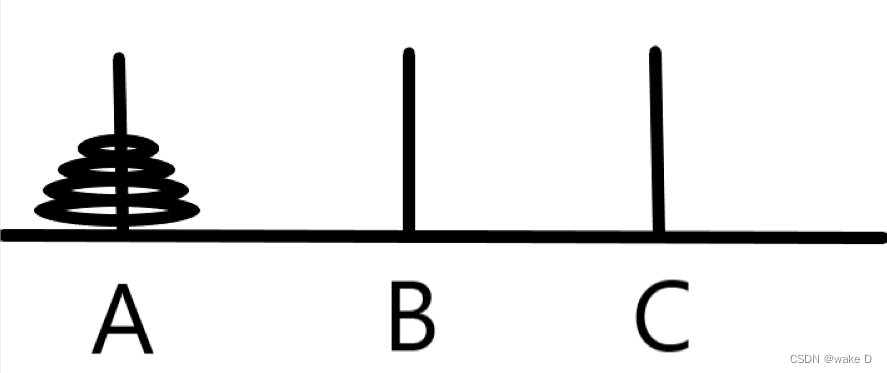
汉诺塔问题,是心理学实验研究常用的任务之一。该问题的主要材料包括三根高度相同的柱子和一些大小及颜色不同的圆盘,三根柱子分别为起始柱A、辅助柱B及目标柱C。
相传在古印度圣庙中,有一种被称为汉诺塔(Hanoi)的游戏。该游戏是在一块铜板装置上,有三根杆(编号A、B、C),在A杆自下而上、由大到小按顺序放置64个金盘(如图1)。游戏的目标:把A杆上的金盘全部移到C杆上,并仍保持原有顺序叠好。操作规则:每次只能移动一个盘子,并且在移动过程中三根杆上都始终保持大盘在下,小盘在上,操作过程中盘子可以置于A、B、C任一杆上。


言归正传,汉诺塔问题的核心其实就是把上面的盘子移动到第三个柱子(辅助柱)上,然后把最底下的盘子移动到目标柱上,再把原先的柱子作为辅助柱,将其余盘子放在最大的盘子上。下面是动画演示图:
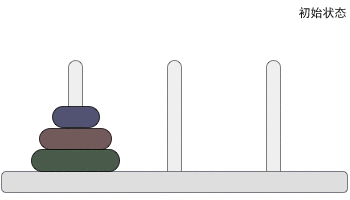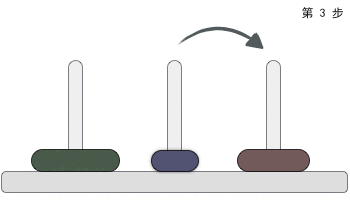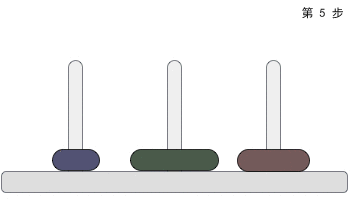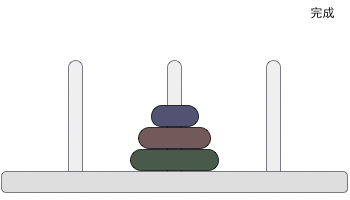
其实怎么做我们高中时候就已经学习过了,那么如何使用C语言来实现上述过程呢?这时候就用到了函数的递归思想,通过函数的嵌套调用,来实现上述过程。下面是C语言的代码以及部分解析:
#include <stdio.h>void Hanoi(int n, char a, char b, char c)//此时a是原柱,b是目标柱,c是辅助柱
{if (n == 1){printf("移动%d:从%c到%c\n", n, a, b);//这个是当只剩下最底下的盘子时,直接移动到目标柱上}else{Hanoi(n - 1, a, c, b);//这个时候a是原柱,c是目标柱,b是辅助柱printf("移动%d:从%c到%c\n", n, a, b);//移动完上面的柱子后把最底下的柱子移动走Hanoi(n - 1, c, b, a);//这个时候c是原柱,b是目标柱,a是辅助柱}
}
int main()
{int n = 0;printf("输入放上的塔数:");scanf("%d", &n);Hanoi(n,'A', 'B', 'C');return 0;
}上面是代码,下面我们来实现一下,跟着程序结果走一遍,是不是发现不用动脑也可以解出来汉诺塔问题呢?我们以3个盘子为例,从上到下依次标记为1,2,3。同时我们有三个柱子,接下来,跟着程序走吧:
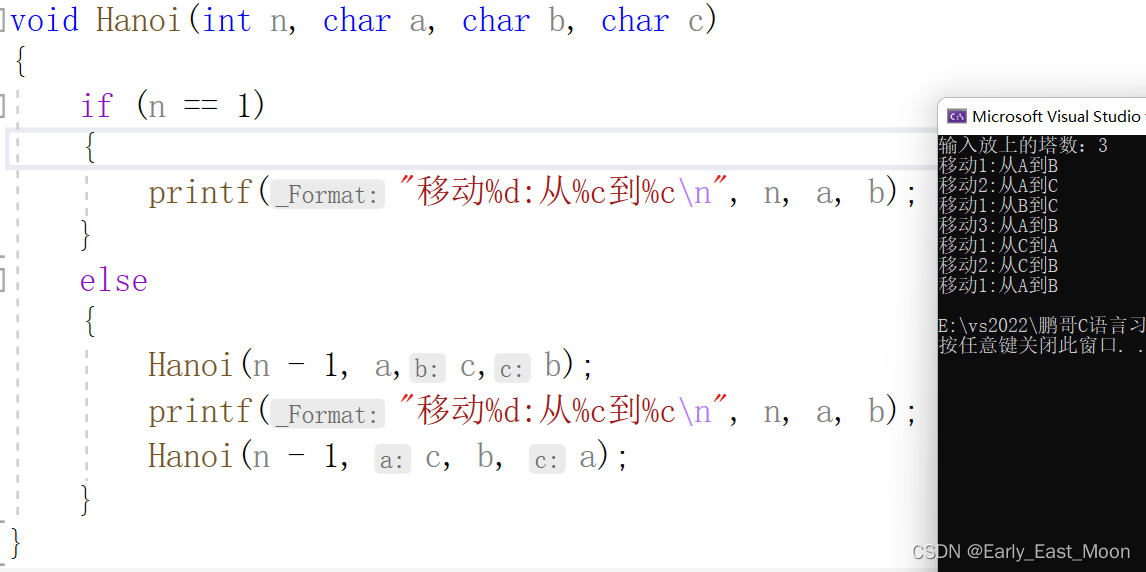

怎么样,是不是感觉C语言来解决这种题方便了许多呢?其实核心就是递归思想,递归作为一种算法在程序设计语言中广泛应用。一个过程或函数在其定义或说明中有直接或间接调用自身的一种方法,他通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。递归的主要思想就是:把大事化小。
是不是很有趣呢?你也来试试吧。如果本文对你有帮助或者觉得有趣,就给一个小红心吧。下期再见。