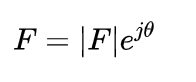0前言

在上一篇博客中，我们详细介绍了矩量法（MoM）的原理及其数值求解过程。在这篇文章中，我们将以电场积分方程（EFIE）为例，介绍基于RWG函数的矩量法C++代码。
在正式解析代码之前，要先提一下关于矢量运算库函数的问题。
在求解EFIE方程的MoM方法中，涉及到了大量的矢量和矩阵运算过程，为了提高我们的编程效率，推荐选择一款成熟的矢量运算库。
这里，给大家推荐armadillo C++。这个运算库的使用方式非常类似Matlab，有matlab经验的人非常容易上手，我这里就不再过多介绍了。另外，我在个人网盘中上传了armadillo的配置和安装教程。感兴趣的朋友可以自行下载，链接如下：https://pan.baidu.com/s/1M0pZF_d56CNyhdF5mK9wZQ。

1三维目标几何剖分与网格信息处理

从上一张的介绍中不难发现，利用MoM求解EFIE，关键难点在于计算并填充阻抗矩阵方程。说白了，就是计算不同RWG函数之间基于电场积分算子联系起来的相互作用效应。那么问题来了，我们怎么将针对一个三维目标定义与其相对应的RWG函数呢？
根据RWG函数的定义，它的本质是依托一对三角面片的公共边定义的。因此，拿到一个三维目标，我们要做的第一步就是对其进行表面三角剖分，将其分解为一系列三角面片的组合。通常，这样的表面三角剖分工作依托一些现有的成熟工具（如FEKO、Ansys ICEM CFD）等就可以开展。
得到目标剖分后的三角面片网格信息之后，我们要对其进行一系列的处理，如定义三角面片编号、定义RWG函数等。这些工作是MoM求解的第一道难关。

2阻抗矩阵计算

阻抗矩阵元素的计算与填充是矩量法的核心，上一篇博客中有详细的说明，这里就不再详细说明了。需要补充说明的一点是，目标的阻抗矩阵主要决定因素就是目标的网格剖分信息。

3激励矩阵填充与表面电流求解

关于激励矩阵，实质上就是目标表面定义的RWG函数与入射波的相互作用，故而其除了与目标的网格剖分信息相关之外，还与入射波的方向、极化方式相关。另外，程序求解出的表面电流I实际上并不是目标的表面电流密度，它只是RWG函数的系数，两者合在一起才是严格意义上的表面电流密度。

4根据目标表面电流计算空间散射场及RCS

计算得到目标表面电流系数之后，就可以根据自由空间电流源的散射场公式计算目标在照射波条件下的空间散射场及其他电磁特征。这里，在计算目标空间散射场的过程中，采用的偶极子等效法，及目标表面的RWG函数等效成一系列电偶极子。具体的过程鉴于时间关系就不再这里详述，感兴趣的朋友可以参考论文：《综合函数矩量法理论及应用研究》。

5示例代码与说明

以下是利用Matlab编写的一段演示金属球体双站RCS计算的代码。代码主要分为三个部分：第一部分是利用Matlab生成一个半径为factor*lambda的金属球，并利用delaunayTriangulation函数对该金属球进行表面三角剖分，获取剖分网格信息；第二部分是设置照射波的参数（本例为一线极化平面波），并利用MoM计算金属球的双站RCS；第三部分是结果可视化。
第二部分关于MoM的代码是利用C++严格按照上一篇博客的思路编写的，这是一个通用的MoM程序，只需输入目标的三角剖分网格信息和对应的照射波参数即可直接计算目标的散射特性曲线。完整的源码已上传本站https://download.csdn.net/download/u014411646/12420361。

clc;clear all;close all;
f = 1e9;
c0 = 3e8;
lambda = c0/f;
step = lambda/10;
factor = 1.5;
%% sphere 创建目标三角剖分网格 
R = factor * lambda;
Jl = pi*R;
N_theta = round(Jl/step);
theta = 0 : pi/N_theta : pi;
X = []; Y = []; Z = [];
for n = 1 : length(theta)th = theta(n);if abs(th-0)<1e-4X(end+1) = 0; Y(end+1) = 0; Z(end+1) = R;elseif abs(th-pi)<1e-4X(end+1) = 0; Y(end+1) = 0; Z(end+1) = -R;elser = R*sin(th);Wl = 2*pi*r;if Wl <= 2*stepX(end+1) = r*cos(0); Y(end+1) = r*sin(0); Z(end+1) = R*cos(th);X(end+1) = r*cos(pi); Y(end+1) = r*sin(pi); Z(end+1) = R*cos(th);elseN_phi = round(Wl/step);phi = 0 : 2*pi/N_phi : 2*pi;for m = 1 : length(phi)X(end+1) = r*cos(phi(m)); Y(end+1) = r*sin(phi(m)); Z(end+1) = R*cos(th);endendend    
end
X = X(:); Y = Y(:); Z = Z(:);
DT = delaunayTriangulation(X,Y,Z);
[tdata,v] = convexHull(DT);
pdata = [X Y Z];
trisurf(tdata, X, Y, Z,'FaceAlpha',1.0);axis equal;box on;
xlabel('x'); ylabel('y'); zlabel('z');
p_whole = 'pdata_whole.txt';
t_whole = 'tdata_whole.txt';
save(p_whole,'pdata','-ascii');
save(t_whole,'tdata','-ascii');
%% MoM计算目标RCS
RCS_plane = 1;
dz = [-1.0 0.0 0.0];
Pol = [0.0 0.0 1.0];
fid = fopen('InputPara_MoM.txt','w');
fprintf(fid,p_whole);fprintf(fid,' ');fprintf(fid,t_whole);fprintf(fid,'\r\n');
fprintf(fid,'freq: ');fprintf(fid,num2str(f));fprintf(fid,'\r\n');
fprintf(fid,'RCS_plane: ');fprintf(fid,num2str(RCS_plane));fprintf(fid,'\r\n');
fprintf(fid,'dz: ');fprintf(fid,num2str(dz));fprintf(fid,'\r\n');
fprintf(fid,'Pol: ');fprintf(fid,num2str(Pol));fprintf(fid,'\r\n');
fclose(fid);
system('MoM_EFIE.exe');
%% 结果可视化
figure;
theta = -180:180;
rcs_mom = importdata('BiRCS_xoz_MoM.txt');
plot(theta,rcs_mom,'b');hold off;
grid on; xlabel('theta/deg');ylabel('BiRCS/dBsm');

利用上述程序，我们计算了金属球的双站RCS曲线，结果如下所示。