相量的加减乘除计算
矢量是物理学中的术语,是指具有大小(magnitude)和方向的量。如速度、加速度、力等等就是这样的量。向量是数学中的术语,也称为欧几里得向量、几何向量、矢量。与向量对应的量叫做数量,在物理学中称为标量,数量只有大小,没有方向。
相量是电子工程学中用以表示正弦量大小和相位的矢量。它仅用来表示具有正弦波的电压和电流,将电压电流用一个复数形式表示,以方便计算。为了让这两个相量相乘具有功率的意义,在极坐标系中,使用电压和电流的有效值来表示相量的大小表示,相量的角度使用电压电流的初相角。不再象直角坐标系,采用幅值和正弦函数的乘积来表示。
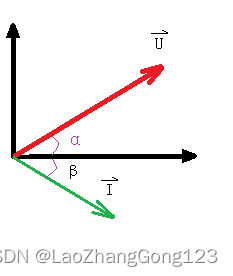
由于电压和电流同频,我们将电压相量和电流相量画在同一个复平面中(极坐标系),称为相量图。
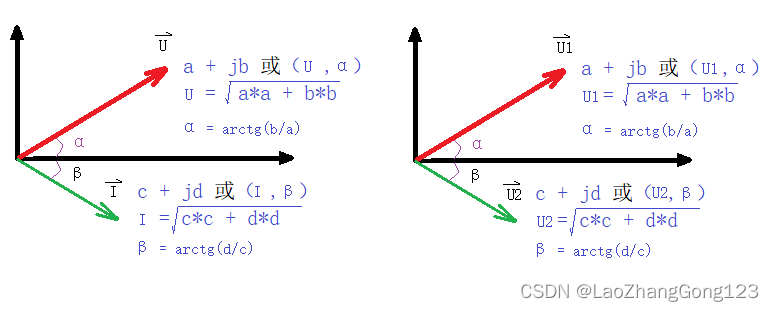
在上图中:
相量U = a + jb = U * [cos(α)+ jsin(α)]
相量I = c + jd = I * [cos(β)+ jsin(β)]
相量U1 = a + jb = U1 * [cos(α)+ jsin(α)]
相量U2 = c + jd = U2 * [cos(β)+ jsin(β)]
采用有效值表示相量的大小,是因为考虑到功率计算,如果继续使用幅值表示相量的大小,会导致电压电流相量的乘积就失去了功率的意义,因此,这里采用有效值表示相量的大小。采用初相角表示方向,是因为电压电流相量同频。
相量加法

相量U1 + 相量U2 = U1 * [cos(α)+ jsin(α)] + U2 * [cos(β)+ jsin(β)]
= [U1 * cos(α)+ U2 * cos(β)] + j[U1 * sin(α)+ U2 * sin(β)]
相量和模的平方:
[U1 * cos(α)+ U2 * cos(β)]* [U1 * cos(α)+ U2 * cos(β)]+ [U1 * sin(α)+ U2 * sin(β)]* [U1 * sin(α)+ U2 * sin(β)]
= U1*U1 + U2*U2 + 2U1*U2*[cos(α) cos(β) + sin(α) sin(β)]
=U1*U1 + U2*U2 + 2U1*U2*cos(α-β)
相量和的角度:
arctg{[U1 * sin(α)+ U2 * sin(β)] /[U1 * cos(α)+ U2 * cos(β)]}
相量加法结论:相量的实部和实部相加,虚部和虚部相加
相量减法
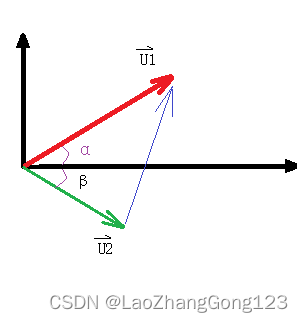
相量U1 - 相量U2 = U1 * [cos(α)+ jsin(α)] - U2 * [cos(β)+ jsin(β)]
= [U1 * cos(α)- U2 * cos(β)] + j[U1 * sin(α)- U2 * sin(β)]
相量和模的平方:
[U1 * cos(α)- U2 * cos(β)]* [U1 * cos(α)- U2 * cos(β)]+ [U1 * sin(α)- U2 * sin(β)]* [U1 * sin(α)- U2 * sin(β)]
= U1*U1 + U2*U2 - 2U1*U2*[cos(α) cos(β) + sin(α) sin(β)]
=U1*U1 + U2*U2 - 2U1*U2*cos(α-β)
相量和的角度:
arctg{[U1 * sin(α)- U2 * sin(β)] /[U1 * cos(α)- U2 * cos(β)]}
相量减法结论:相量的实部和实部相减,虚部和虚部相减
相量乘法
相量U和相量I的乘积=[U*cos(α)+jU*sin(α)] * [I*cos(β)+jI*sin(β)]
=UI{[cos(α)cos(β)-sin(α)sin(β)] + j [cos(α) sin(β)+sin(α) cos(β)]}
=UI[cos(α+β) + jsin(α+β)]
相量乘法结论:“积的模”等于相量的模相乘,“积的角度”等于相量的角度相加。
有功功率计算

有功功率功是“电流的有功分量”乘以“电压相量的模”,因此,有功功率为UIcos(α-β)。
相量除法
相量U和相量I的商=[U*cos(α)+jU*sin(α)] / [I*cos(β)+jI*sin(β)]
=(U/I)* [cos(α)+jsin(α)] / [cos(β)+jsin(β)]
=(U/I)* [cos(α)+jsin(α)] *[cos(β)-jsin(β)]/ {[cos(β)+jsin(β)]* [cos(β)-jsin(β)]}
=(U/I)* [cos(α)+jsin(α)] *[cos(β)-jsin(β)]
=(U/I)* [cos(α)cos(β)+ sin(α) sin(β)]+j[sin(α)cos(β)-cos(α)sin(β)]
=(U/I)* [cos(α-β)+jsin(α-β)]
相量除法结论:“商的模”等于相量的模相除,“商的角度”等于相量的角度相减。
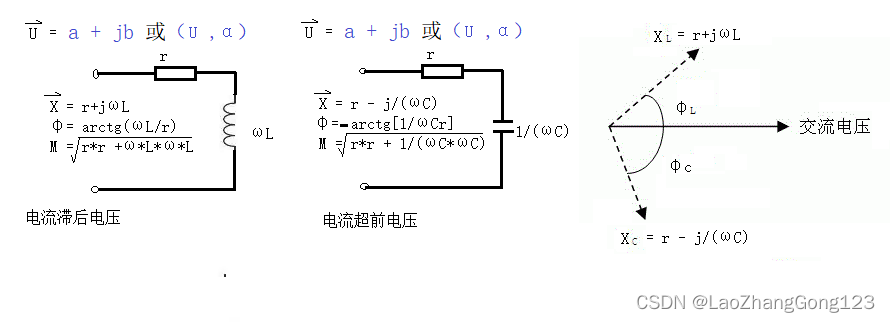
复阻抗的相位角φ,阻抗是复阻抗的模,容抗为1/ωC,感抗为ωL
电压相量为U[cos(α)+jsin(α)]
复阻抗是一个复数,为M[cos(φ)+jsin(φ)]
电流相量= U[cos(α)+jsin(α)] / M[cos(φ)+jsin(φ)]
=(U/M)* [cos(α)+jsin(α)] / [cos(φ)+jsin(φ)]
=(U/M)* [cos(α)+jsin(α)] * [cos(φ)-jsin(φ)]
=(U/M)*{[cos(α)cos(φ) + sin(α)sin(φ)]+j[sin(α)cos(φ)- cos(α)sin(φ) }
=(U/M)*{[cos(α-φ)]+j[sin(α-φ) }
电流初相角为 (α-φ),即电流初相角等于电压初相角与复阻抗角度的差。
因此,当φ> O时,电流初相角小于电压初相角,即电流滞后电压;当φ< O时,电流初相角大于电压初相角,即电流超前电压。
电压电流相位差ψ=α-(α-φ)= φ,即电压电流相位差等于复阻抗的角度值。
因此,功率因素等于阻抗角度的余弦值,等于电压电流相位差的余弦值。知道了功率因素,就等于告诉了复阻抗的角度值。
很多学习《电路分析》的人,不知道“视在功率等于电压相量乘以电流相量的共轭”。记得上课时,教授给出他的证明过程,我疑惑不已,以为他在凑答案。估计很多人讲不清楚其中的原因。
证明:视在功率等于电压相量乘以电流相量的共轭
已知:电压相量为(U, α), 复阻抗为M[cos(φ)+jsin(φ)]
经过计算:电流初相角为β=(α-φ),I=U/M,得到φ=α-β
根据视在功率等于电压相量的平方除法以复阻抗,得到:
[U*cos(α)+jU*sin(α)] * [U*cos(α)+jU*sin(α)] / M*cos(φ)+jM*sin(φ)]
=U*U*[cos(2α)+ jsin(2α)] / [M*cos(φ)+jM*sin(φ)]
=(U*U/M)* [cos(2α)+ jsin(2α)]* [cos(φ) - jsin(φ)]
=(U*U/M)* [cos(2α)+ jsin(2α)] * [cos(-φ) + jsin(-φ)]
=(U*U/M)* [cos(2α-φ)+ jsin(2α-φ)]
=(U*I)* {cos[2α-(α-β)]+ jsin[2α-(α-β)]}
=(U*I)* [cos(α-β)+ jsin(α-β)]
实部为UIcos(α-β),表示有功功率,虚部为UI sin(α-β),表示无功功率。
因此,视在功率等于电压相量乘以电流相量的共轭。
基尔霍夫第一定律又称基尔霍夫电流定律,简记为KCL,其物理背景是电荷守恒公理。假设进入某节点的电流为正值,离开这节点的电流为负值,则所有涉及这节点的电流的代数和等于零,因此又称为节点电流定律。
基尔霍夫第二定律又称基尔霍夫电压定律,简记为KVL,其物理背景是能量守恒。沿着闭合回路所有元件两端的电势差(电压)的代数和等于零,因此又称为回路电压定律。