简介

相信大家在学习《电路》这门课程的时候就遇到了神奇的相量法，
自1893年由德国人C.P.施泰因梅茨提出后，这种牛逼的方法就大
受欢迎。本来求解正弦稳态电路的稳态解的时候，需要根据电路
列写微分方程，然后对微分方程求解。但是使用相量法之后，电
感和电容原件竟然可以像电阻一样处理计算，可谓是大大简化了
求解过程。这些都是教科书告诉我们的内容，可是相量法却有使
用限制：

1. 激励源必须是正弦信号（当然其他周期信号可以通过傅里叶分
   解得到一系列不同频率正弦信号的组合）
2. 只能用于线性电路，若电路含有非线性原件就不适用了。

那么，相量法对正弦稳态电路得到的解就是电路的解吗？在写这
篇博文的以前我一直深信不疑，知道遇到了下面的例子。

一个例子

$U_s=sin(t),L=1H,C=1F,R=1\Omega$ 求电容上的电压 $U_c$

先不理具体参数，使用相量法：
$\dot{U_s}=\frac{\sqrt{2}}{2}\angle 0^{\circ }$

$\frac{\dot{U_c}}{\dot{U_s}}=\frac{1}{1-{\omega }^{2}LC+j\omega RC}$

$\dot{U_c}=\frac{\sqrt{2}}{2\sqrt{(1-{\omega }^{2}LC{)}^2+(\omega RC{)}^2}}\angle arctan(\frac{\omega RC}{1-{\omega }^{2}LC})\times 180^{\circ }÷\pi$

带入参数解得： $\dot{U_c}=\frac{\sqrt{2}}{2}\angle -90^{\circ }$
可知 $U_c=sin(t-90^{\circ })$

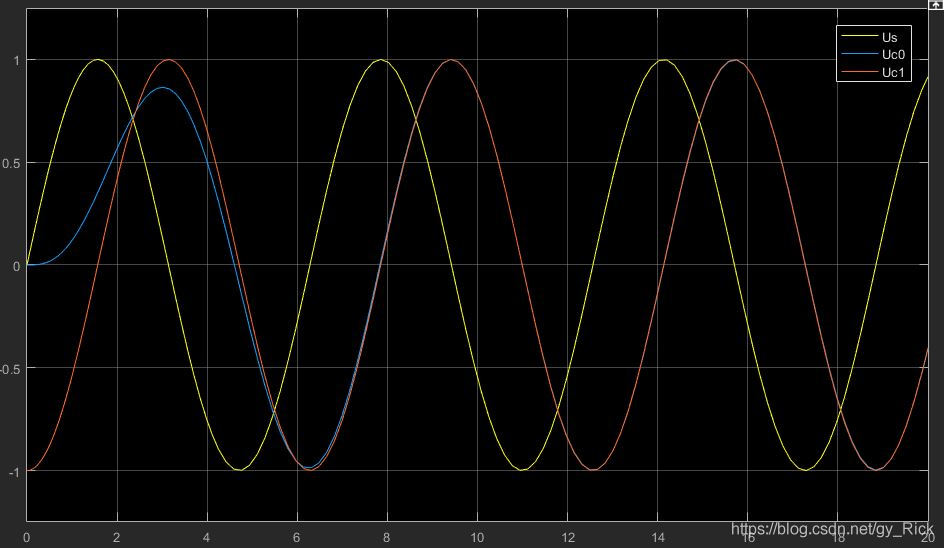
然后看图：

其中Uc0为仿真得到的 $U_c$ 曲线，Uc1为计算得到的预期曲线，为啥一开始他们不是重合的呢？？？原来相量法得到的是稳态解啊！！正因为如此它才用来求解正弦稳态电路。只要时间够长，他们（曲线）就会重合的！！

我们对刚刚那组参数求解微分方程：
$U_c=e^{-\frac{t}{2}}(cos(\frac{\sqrt{3}}{2}t)+\frac{\sqrt{3}}{3}sin(\frac{\sqrt{3}}{2}t))+sin(t-90^{\circ })$
可见使用相量法求解会少了前面的衰减项，导致刚开始曲线不重合，但由于第一项衰减很快，因此曲线很快就重合。那是否能说，相量法求解的就是正弦稳态电路的稳态解呢？是否时间够长一定能看到曲线重合呢？？

另一个例子

$U_s=sin(t),L=1H,C=1F$ 求电容上的电压 $U_c$ （去掉电阻）

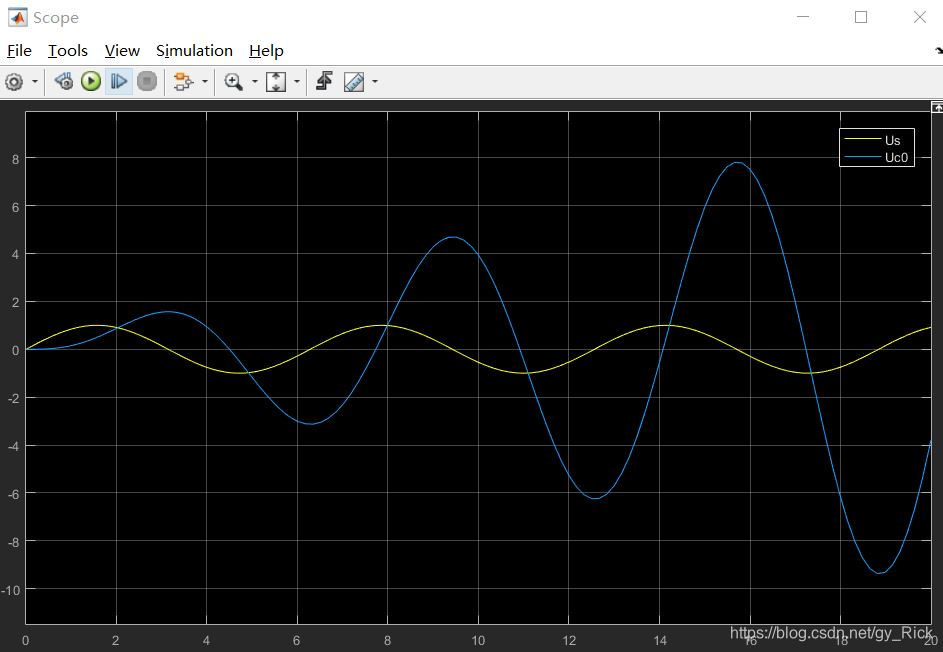
让我们首先看一下 $U_c$ 仿真图：

这下可能我们一下子就明白了，如果电路本身就是不稳定的，那么相量法自然也得不到稳态解。

$\frac{\dot{U_c}}{\dot{U_s}}=\frac{1}{1-{\omega }^{2}LC}\to \infty$

从式子我们可以猜测，稳态解为幅值正无穷，相位不变的正弦波。

求解微分方程：
$U_c=\frac{3sin(t)-sin(3t)}{8}-(\frac{t}{2}-\frac{1}{4}sin(2t))cos(t)$
可见不稳定的电路还产生了意料之外的2、3次谐波。那是否稳定的（不发散）电路相量法就一定能求到其稳态解，曲线就会重合呢？？

再来一个例子

继续改变参数：
$U_s=sin(t),L=0.1H,C=1F$ 求电容上的电压 $U_c$ （去掉电阻）

这次我们认为结论一定是对的，因此先求解再看仿真：

$\frac{\dot{U_c}}{\dot{U_s}}=\frac{1}{1-{\omega }^{2}LC}=1.11$
$\dot{U_c}=0.785\angle 0^{\circ }$
$U_c=1.11sin(t)$

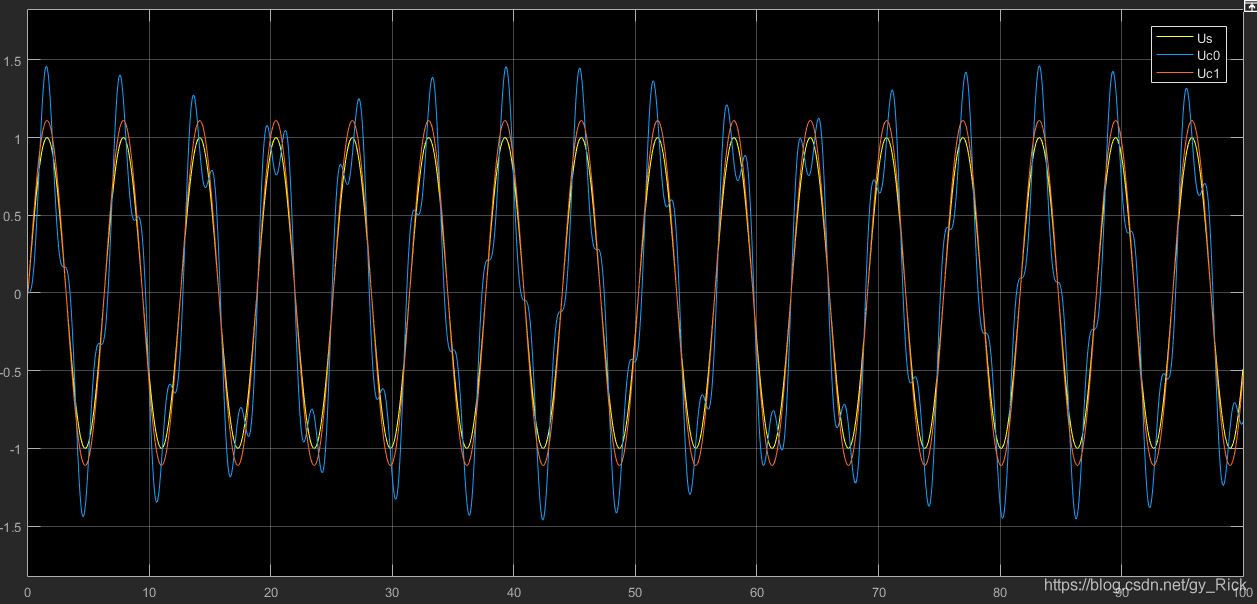
看到这结果可真让人大跌眼镜，为啥得到的 $U_c$ 曲线这么奇葩。
我们不得不求一下微分方程：

$U_c=\frac{10}{9}sin(t)-\frac{\sqrt{10}}{9}sin(\sqrt{10}t)$

从微分方程解中我们知道，第一项确实是我们用相量法求出的结果，但还有另外一项非整数次谐波的出现，真让人意外，而这个结果是有界的，也可以说是稳定的吧，但第二项却并不会衰减，一直随时间加在第一项上。

结论

1. 查阅百度百科，稳态的解释为:在某一输入信号的作用后，时间趋于无穷大时系统的输出状态称为稳态。而对于最后一个例子，即便时间趋于无穷大，奇怪的谐波依然会如影随形，在这个意义上，就不能说相量法求出的是稳态解。
2. 微分方程的解分为通解和特解，但可以肯定的是，相量法确实求出了微分方程的特解。但特解是否等价与稳态解，这还值得商榷吧？？
3. 那为什么很多书都默认了相量法求出的解就是正弦稳态电路的稳态解呢？是因为在日常生活中，电路不可能没有电阻。我们在考虑一下相量法适用的条件2（线性电路），线性电路可以使用叠加定理。则考虑： 解=零状态响应 + 零输入响应。相量法求出了零状态响应，但对于零输入响应，如果电路无耗能原件（如电阻），那么尽管无激励源，电路内部的能量也不会消耗，只会在电容电感元件上互相传递，因此这一项就永远不会衰减，然而即便没有电阻，现实生活中也不可能存在永远不会衰减这种情况，电容电感本身就会消耗微小能量。
4. 因此，相量法可以求解正弦稳态电路的稳态解还是对的，但是却绝不能求出暂态解，这却是很多朋友忽略的。

引用

1. 《电路》 邱关源著。
2. 党建亮，林爱英，朱连轩，吴丽丽，袁超. 相量法与傅里叶变换的联系与区别