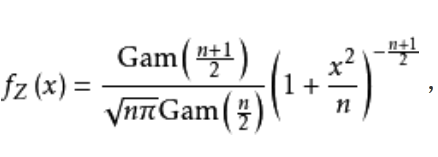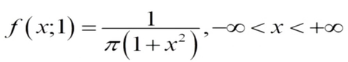统计量的分布称为 抽样分布,在使用统计量进行统计推断时需要知道它的分布,当总体的分布函数已知时,抽样分布是确定的,然而要求出统计量的精确分布,一般来说是困难的,下面介绍来自正态总体的几个常用统计量的分布.
1. χ 2 \chi^2 χ2 分布
-
定义
设 X 1 , X 2 , ⋯ , X n X_1,X_2,\cdots,X_n X1,X2,⋯,Xn 是来自总体 N ( 0 , 1 ) N(0,1) N(0,1)的样本,则称统计量 χ 2 = ∑ i = 1 n X i 2 , i = 1 , 2 , 3 ⋯ , n \chi^2 = \sum\limits_{i=1}^{n}X_i^2,\quad i = 1,2,3\cdots,n χ2=i=1∑nXi2,i=1,2,3⋯,n 服从自由度为 n n n的 χ 2 \chi^2 χ2分布,记为 χ 2 ∼ χ 2 ( n ) . \chi^2\sim\chi^2(n). χ2∼χ2(n).
此处的自由度是指独立变量的个数
-
χ 2 \chi^2 χ2分布的概率密度
f ( y ) = { 1 2 n / 2 Γ ( n / 2 ) y n / 2 − 1 e − y / 2 , y > 0 0 , e l s e f(y) = \begin{cases} \frac{1}{2^{n/2}\Gamma(n/2)}y^{n/2-1}e^{-y/2},\quad y>0 \\\\0, \quad else\end{cases} f(y)=⎩⎪⎨⎪⎧2n/2Γ(n/2)1yn/2−1e−y/2,y>00,else
其图像如下

- 图像为单峰曲线
- 图像为非对称图形
- n > 2 n>2 n>2时,在 n − 2 n-2 n−2处取得最大值
- n n n越大,峰越往右,图像也越趋于对称,当 n n n很大时,可近似看做正态分布
-
χ 2 \chi^2 χ2分布性质
-
χ 2 \chi^2 χ2分布的可加性
设 χ 1 2 ∼ χ 2 ( n 1 ) , χ 2 2 ∼ χ 2 ( n 2 ) \chi_1^2 \sim \chi^2(n_1),\chi_2^2 \sim \chi^2(n_2) χ12∼χ2(n1),χ22∼χ2(n2),并且 χ 1 2 , χ 2 2 \chi_1^2,\chi_2^2 χ12,χ22相互独立,则有 χ 1 2 + χ 2 2 ∼ χ 2 ( n 1 + n 2 ) \begin{aligned} \chi_1^2+\chi_2^2 \sim \chi^2(n_1+n_2) \end{aligned} χ12+χ22∼χ2(n1+n2)
-
χ 2 \chi^2 χ2分的数学期望和方差
E ( χ 2 ) = n , D ( χ 2 ) = 2 n . E(\chi^2)=n,D(\chi^2)=2n. E(χ2)=n,D(χ2)=2n.
证明:
由于 χ 2 = ∑ i = 1 n X i 2 \chi^2 = \sum\limits_{i=1}^{n}X_i^2 χ2=i=1∑nXi2,其中 X i ∼ N ( 0 , 1 ) X_i \sim N(0,1) Xi∼N(0,1) ,因此有
E ( X i 2 ) = D ( X i ) + ( E X i ) 2 = 1 + 0 = 1 E(X_i^2) = D(X_i)+(EX_i)^2 = 1+0=1 E(Xi2)=D(Xi)+(EXi)2=1+0=1
因此 E ( χ 2 ) = n ∗ E ( X i 2 ) = n E(\chi^2) = n*E(X_i^2) = n E(χ2)=n∗E(Xi2)=n
D ( χ 2 ) = n ∗ D ( X i 2 ) = n ∗ [ E ( X i 2 ) 2 − E ( X i 2 ) ] = n ∗ [ E ( X i 4 ) − E ( X i 2 ) ] = n E ( X i 4 ) − n \begin{aligned} D(\chi^2) &= n*D(X_i^2) \\&= n*[E(X_i^2)^2-E(X_i^2)] \\&= n*[E(X_i^4)-E(X_i^2)] \\&=nE(X_i^4)-n\end{aligned} D(χ2)=n∗D(Xi2)=n∗[E(Xi2)2−E(Xi2)]=n∗[E(Xi4)−E(Xi2)]=nE(Xi4)−n
我们需要知道 E ( X i 4 ) E(X_i^4) E(Xi4), 目前没有更好的方式,我们尝试使用期望的定义进行计算
E ( X i 4 ) = ∫ − ∞ + ∞ x 4 1 2 π e − x 2 2 d x = 1 2 π ∫ − ∞ + ∞ x 4 e − x 2 2 d x = 1 2 π [ − x 3 e − x 2 2 ∣ − ∞ + ∞ + ∫ − ∞ + ∞ 3 x 2 e − x 2 2 d x ] = 0 + 3 ∫ − ∞ + ∞ 1 2 π x 2 e − x 2 2 d x = 3 ∫ − ∞ + ∞ x 2 1 2 π e − x 2 2 d x \begin{aligned} E(X_i^4) &= \int_{-\infty}^{+\infty}x^4\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx \\&= \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}x^4e^{-\frac{x^2}{2}}dx \\&= \frac{1}{\sqrt{2\pi}}\bigg[-x^3e^{-\frac{x^2}{2}}\bigg|_{-\infty}^{+\infty}+\int_{-\infty}^{+\infty}3x^2e^{-\frac{x^2}{2}}dx\bigg] \\&=0+3\int_{-\infty}^{+\infty}\frac{1}{\sqrt{2\pi}}x^2e^{-\frac{x^2}{2}}dx \\&= 3\int_{-\infty}^{+\infty}x^2\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\end{aligned} E(Xi4)=∫−∞+∞x42π1e−2x2dx=2π1∫−∞+∞x4e−2x2dx=2π1[−x3e−2x2∣∣∣∣−∞+∞+∫−∞+∞3x2e−2x2dx]=0+3∫−∞+∞2π1x2e−2x2dx=3∫−∞+∞x22π1e−2x2dx
这里对后面的积分项可继续采用分部积分方法进行处理,但是这地方其实有个技巧 ,根据期望定义有
E ( X i 2 ) = ∫ − ∞ + ∞ x 2 1 2 π e − x 2 2 d x \begin{aligned} E(X_i^2) = \int_{-\infty}^{+\infty}x^2\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx \end{aligned} E(Xi2)=∫−∞+∞x22π1e−2x2dx
前面我们已经算出 E ( X i 2 ) = 1 E(X_i^2)=1 E(Xi2)=1
因此有 E ( X i 2 ) = ∫ − ∞ + ∞ x 2 1 2 π e − x 2 2 d x = 1 \begin{aligned} E(X_i^2) = \int_{-\infty}^{+\infty}x^2\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx=1 \end{aligned} E(Xi2)=∫−∞+∞x22π1e−2x2dx=1
所以有 E ( X i 4 ) = 3 ∗ 1 = 3 E(X_i^4) = 3*1 = 3 E(Xi4)=3∗1=3
∴ D ( χ 2 ) = n E ( X i 4 ) − n = 3 n − n = 2 n \therefore D(\chi^2) = nE(X_i^4)-n = 3n-n=2n ∴D(χ2)=nE(Xi4)−n=3n−n=2n
-
-
χ 2 \chi^2 χ2分布的分位点
对于给定的正数 α , 0 < α < 1 \alpha,\quad 0<\alpha<1 α,0<α<1,称满足条件 P { χ 2 > χ α 2 ( n ) } = ∫ χ α 2 ( n ) ∞ f ( y ) d y = α \begin{aligned} P\{\chi^2>\chi_\alpha^2(n)\} = \int_{\chi_\alpha^2(n)}^{\infty}f(y)dy = \alpha \end{aligned} P{χ2>χα2(n)}=∫χα2(n)∞f(y)dy=α 的点 χ α 2 ( n ) \chi_\alpha^2(n) χα2(n)为 χ 2 ( n ) \chi^2(n) χ2(n)分布的上 α \alpha α分位点
-
补充 Γ \Gamma Γ函数介绍
Γ ( x ) = ∫ 0 ∞ t x − 1 e − t d t . ( x > 0 ) \begin{aligned}\Gamma(x) = \int_0^{\infty}t^{x-1}e^{-t}dt.\quad(x>0)\end{aligned} Γ(x)=∫0∞tx−1e−tdt.(x>0)
-
性质 1 1 1
Γ ( x + 1 ) = x Γ ( x ) \begin{aligned}\Gamma(x+1) = x\Gamma(x)\end{aligned} Γ(x+1)=xΓ(x)
- 推论1
Γ ( 2 ) = Γ ( 1 ) = 1 \Gamma(2)=\Gamma(1)=1 Γ(2)=Γ(1)=1
- 推论2
Γ ( 1 2 ) = π \Gamma(\frac{1}{2}) = \sqrt\pi Γ(21)=π
- 推论3
Γ ( n + 1 ) = n ! \Gamma(n+1) = n! Γ(n+1)=n!
-
性质2
对于 0 < x < 1 , Γ ( 1 − x ) Γ ( x ) = π s i n π x 0 <x <1,\quad\Gamma(1-x)\Gamma(x)=\frac{\pi}{sin\pi x} 0<x<1,Γ(1−x)Γ(x)=sinπxπ
-
-
补充 Γ \Gamma Γ分布介绍
Γ \Gamma Γ分布是统计学的一种连续概率函数,是概率统计中一种非常重要的分布。指数分布和χ2分布都是伽马分布的特例
-
假设随机变量 X X X为等到第 α \alpha α件事发生所需的等候时间, 密度函数为
f ( x , β , α ) = β α Γ ( α ) x α − 1 e − β x , x > 0 \begin{aligned} f(x,\beta,\alpha) = \frac{\beta^\alpha}{\Gamma(\alpha)}x^{\alpha-1}e^{-\beta x},\quad x>0 \end{aligned} f(x,β,α)=Γ(α)βαxα−1e−βx,x>0
其中参数 α \alpha α为形状参数, β \beta β 为逆尺度参数
-
E ( X ) = α β , D ( X ) = α β 2 E(X) = \frac{\alpha}{\beta},D(X)=\frac{\alpha}{\beta^2} E(X)=βα,D(X)=β2α
-
Γ \Gamma Γ分布具有可加性
-
当形状参数α=1时,伽马分布就是参数为 β \beta β的指数分布,即 X ∼ E ( β ) X\sim E(\beta) X∼E(β)
-
当 α = n 2 , β = 1 2 \alpha=\frac{n}{2},β=\frac{1}{2} α=2n,β=21时,伽马分布就是自由度为 n n n的卡方分布,即 X ∼ χ 2 ( n ) X\sim \chi^2(n) X∼χ2(n)
-
2. t t t分布
-
定义
设 X ∼ N ( 0 , 1 ) , Y ∼ χ 2 ( n ) X\sim N(0,1),Y\sim \chi^2(n) X∼N(0,1),Y∼χ2(n),且 X , Y X,Y X,Y相互独立,则称随机变量 t = X Y / n t=\frac{X}{\sqrt{Y/n}} t=Y/nX 服从自由度为 n n n的 t \pmb{t} ttt分布 . 记为 t ∼ t ( n ) . t\sim t(n). t∼t(n).
-
t t t分布概率密度
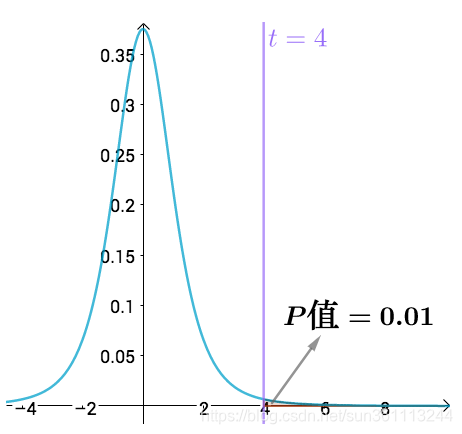
h ( t ) = Γ [ ( n + 1 ) / 2 ] π n Γ ( n / 2 ) ( 1 + t 2 n ) − ( n + 1 ) / 2 , − ∞ < t < ∞ \begin{aligned} h(t) = \frac{\Gamma[(n+1)/2]}{\sqrt{\pi n}\Gamma(n/2)}\bigg(1+\frac{t^2}{n}\bigg)^{-(n+1)/2},\quad -\infty <t<\infty\end{aligned} h(t)=πnΓ(n/2)Γ[(n+1)/2](1+nt2)−(n+1)/2,−∞<t<∞ 其图像如下

-
以0为中心,左右对称的单峰分布;
-
n n n越小,曲线越低平; n n n越大,t分布曲线越接近标准正态分布曲线
-
当 n ≥ 30 n\geq30 n≥30时, t t t分布近似于标准正态分布
-
t t t分布的分位点
对于给定的正数 α , 0 < α < 1 \alpha,\quad 0<\alpha<1 α,0<α<1,称满足条件 P { t > t α ( n ) } = ∫ t α ( n ) ∞ h ( t ) d t = α \begin{aligned} P\{t>t_\alpha(n)\} = \int_{t_\alpha(n)}^{\infty}h(t)dt = \alpha \end{aligned} P{t>tα(n)}=∫tα(n)∞h(t)dt=α 的点 t α ( n ) t_\alpha(n) tα(n)为 t ( n ) t(n) t(n)分布的上 α \alpha α分位点
- 由 h ( t ) h(t) h(t)图像的对称性可知 t 1 − α ( n ) = − t α ( n ) . t_{1-\alpha}(n) = -t_\alpha(n). t1−α(n)=−tα(n).
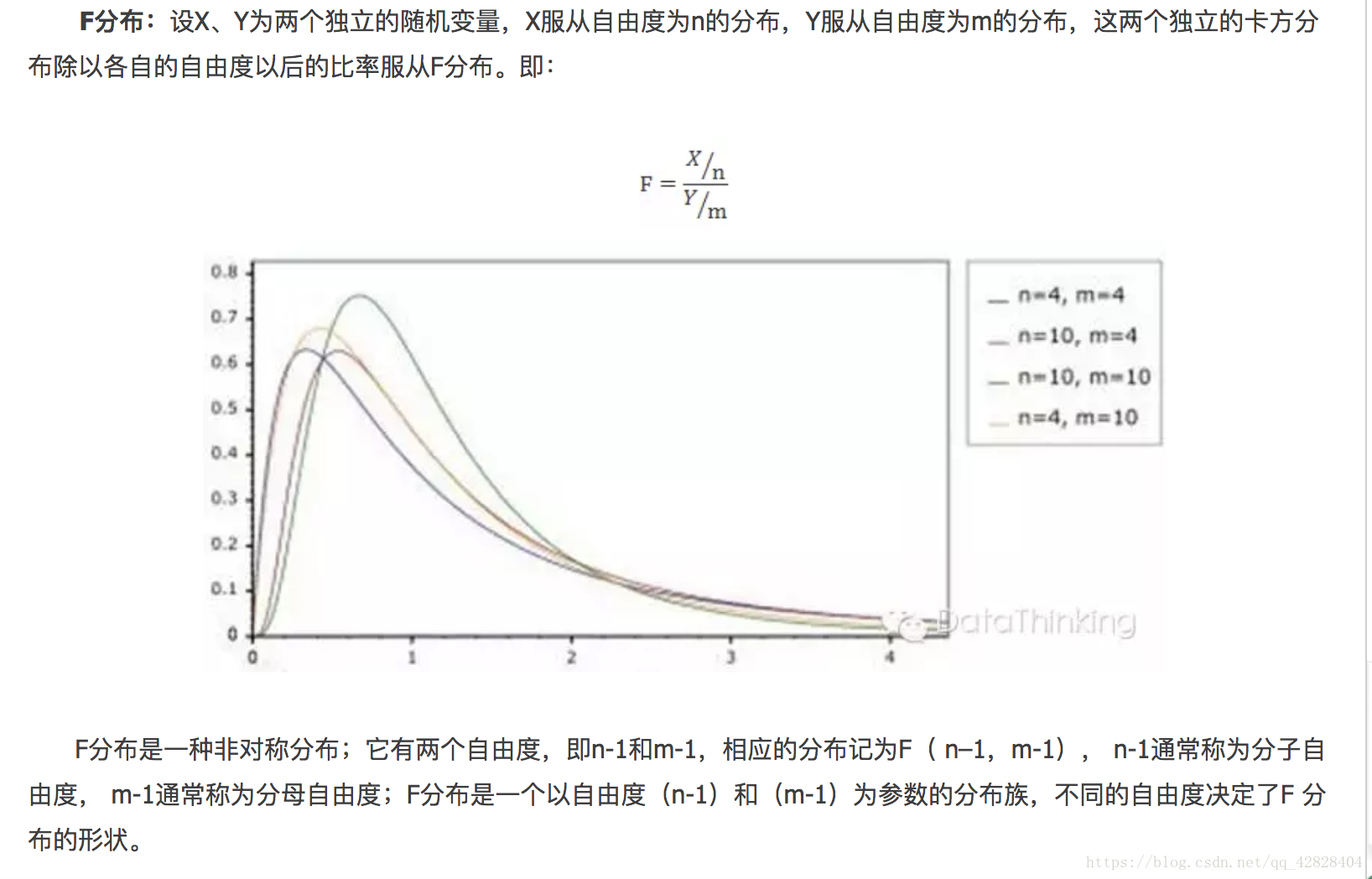
3. F F F分布
-
设 U ∼ χ 2 ( n 1 ) , V ∼ χ 2 ( n 2 ) U\sim \chi^2(n_1),V \sim \chi^2(n_2) U∼χ2(n1),V∼χ2(n2),且 U , V U,V U,V相互独立,则称随机变量 F = U / n 1 V / n 2 F=\frac{U/n_1}{V/n_2} F=V/n2U/n1服从自由度为 ( n 1 , n 2 ) (n_1,n_2) (n1,n2)的 F F F分布,记为 F ∼ F ( n 1 , n 2 ) . F\sim F(n_1,n_2). F∼F(n1,n2).
-
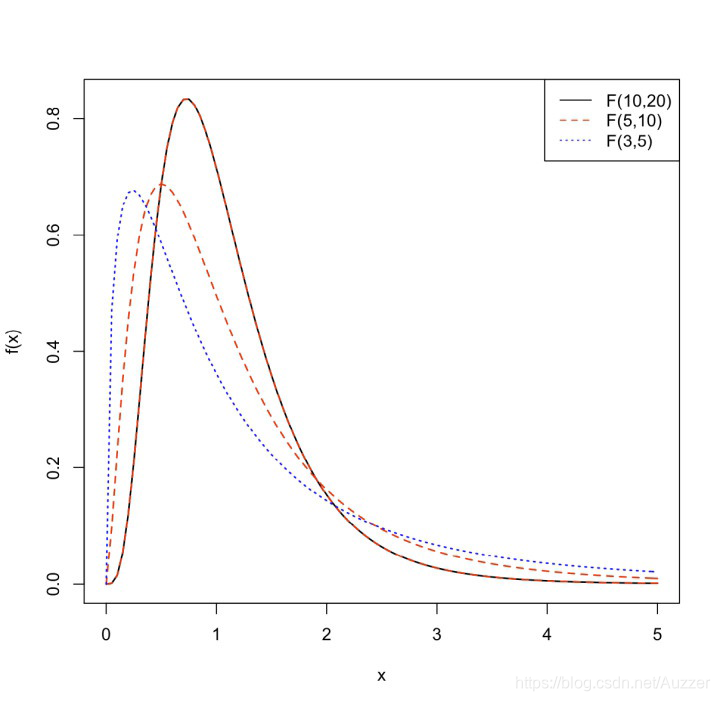
F F F分布概率密度
ψ ( y ) = { Γ [ ( n 1 + n 2 ) / 2 ] ( n 1 / n 2 ) n 1 / 2 y ( n 1 / 2 ) − 1 Γ ( n 1 / 2 ) Γ ( n 2 / 2 ) [ 1 + ( n 1 y / n 2 ) ] ( n 1 + n 2 ) / 2 , y > 0 0 , e l s e \begin{aligned}\psi(y) = \begin{cases} \frac{\Gamma[(n_1+n_2)/2](n_1/n_2)^{n_1/2}y^{(n_1/2)-1} }{\Gamma(n_1/2)\Gamma(n_2/2)[1+(n_1y/n_2)]^{(n_1+n_2)/2}},\quad &y>0 \\\\ 0, &else \end{cases}\end{aligned} ψ(y)=⎩⎪⎨⎪⎧Γ(n1/2)Γ(n2/2)[1+(n1y/n2)](n1+n2)/2Γ[(n1+n2)/2](n1/n2)n1/2y(n1/2)−1,0,y>0else
其图像为

-
由定义可知,若 F ∼ F ( n 1 , n 2 ) F\sim F(n_1,n_2) F∼F(n1,n2),则 1 F ∼ F ( n 2 , n 1 ) \frac{1}{F}\sim F(n_2,n_1) F1∼F(n2,n1)
-
F F F分布的分位点
对于给定的正数 α , 0 < α < 1 \alpha,\quad 0<\alpha<1 α,0<α<1,称满足条件 P { F > F α ( n 1 , n 2 ) } = ∫ F α ( n 1 , n 2 ) ∞ ψ ( y ) d y = α \begin{aligned} P\{F>F_\alpha(n_1,n_2)\} = \int_{F_\alpha(n_1,n_2)}^{\infty}\psi(y)dy = \alpha \end{aligned} P{F>Fα(n1,n2)}=∫Fα(n1,n2)∞ψ(y)dy=α 的点 F α ( n 1 , n 2 ) F_\alpha(n_1,n_2) Fα(n1,n2)为 F ( n 1 , n 2 ) F(n_1,n_2) F(n1,n2)分布的上 α \alpha α分位点.
-
分位点性质
F 1 − α ( n 1 , n 2 ) = 1 F α ( n 2 , n 1 ) . F_{1-\alpha}(n_1,n_2)=\frac{1}{F_\alpha(n_2,n_1)}. F1−α(n1,n2)=Fα(n2,n1)1.
证明如下
根据 F F F分布分位点的定义可知
P { F > F 1 − α ( n 1 , n 2 ) } = 1 − α ∴ P { 1 F < 1 F 1 − α ( n 1 , n 2 ) } = 1 − α 此 时 有 P { 1 F ≥ 1 F 1 − α ( n 1 , n 2 ) } = 1 − ( 1 − α ) = α 再 次 根 据 分 位 数 定 义 , 有 1 F 1 − α ( n 1 , n 2 ) = 1 F α ( n 1 , n 2 ) ∴ F 1 − α ( n 1 , n 2 ) = 1 F α ( n 2 , n 1 ) \begin{aligned} P\{F>F_{1-\alpha}(n_1,n_2) \} &= 1-\alpha \\ \therefore P\{\frac{1}{F}<\frac{1}{F_{1-\alpha}(n_1,n_2)}\} &=1-\alpha \\此时有 P\{\frac{1}{F}\geq \frac{1}{F_{1-\alpha}(n_1,n_2)}\} &=1-(1-\alpha)=\alpha \\再次根据分位数定义,有\frac{1}{F_{1-\alpha}(n_1,n_2)}&=\frac{1}{F_{\alpha}(n_1,n_2)} \\ \therefore F_{1-\alpha}(n_1,n_2)&=\frac{1}{F_\alpha(n_2,n_1)}\end{aligned} P{F>F1−α(n1,n2)}∴P{F1<F1−α(n1,n2)1}此时有P{F1≥F1−α(n1,n2)1}再次根据分位数定义,有F1−α(n1,n2)1∴F1−α(n1,n2)=1−α=1−α=1−(1−α)=α=Fα(n1,n2)1=Fα(n2,n1)1
-