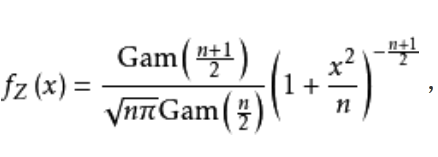1. t检验的历史

  阿瑟·健力士公司（Arthur Guinness Son Co.）是一家由阿瑟·健力士（Arthur Guinness）于1759年在爱尔兰都柏林建立的一家酿酒公司：

  不过它最出名的却不是啤酒，而是《吉尼斯世界纪录大全》：

  1951年11月10日，健力士酒厂的董事休·比佛爵士（Sir Hugh Beaver）在爱尔兰韦克斯福德郡打猎时，因为没打中金鸻，于是和同行们争论哪种鸟飞得最快，彼此争论不休。由于当时的参考资料并不足以回答这个问题，这促使比弗想出版一本记载世界之最的书，这就是后来的《吉尼斯世界纪录大全》。

  在健力士公司，戈斯特提出了t检验以降低啤酒质量监控的成本，但健力士酒厂为了保护公司的商业机密和智慧财产，明文禁止员工发表文章。

  戈斯特并没有因为这项规定而放弃他的学术研究发表，他在《生物统计期刊》以“学生”（The Student）为笔名，发表了关于t检验的文章，所以t检验又称为“学生t检验”。

  直到1937年，戈斯特因心脏病去世之前，健力士酒厂一直不知道戈斯特从事统计研究工作，并以“学生”笔名发表研究成果。许多统计研究者要和戈斯特见面，都必须像间谍电影般地秘密安排见面地点和时间。

  现在位于都柏林的健力士专卖店中有一个戈斯特的纪念碑，上面写著“化学家、统计学家威廉·希利·戈斯特，首席酿酒师，学生t检验”：

2. t检验的思路

  啤酒，主要原料是大麦，啤酒厂肯定是希望尽力提高亩产。

  比如，健力士公司有下面两块麦田：

  左边的麦田采用传统A工艺进行种植，平均每株大麦可以结100粒穗子。

  而右边的麦田采用改进过的B工艺种植，健力士公司想知道“B工艺是否提高了产量”。

  为了节约成本、减小损耗，抠门的健力士公司从B工艺的麦田中采样了5株大麦，样本均值为120粒穗子。然后把难题抛给了戈斯特。

  似乎直观看来产量提高了，毕竟均值增加了20%，可是戈斯特想得更多一些。

2.1 戈斯特的分析

  戈斯特提出一个假设检验

  假设：B工艺没有提高产量，即AB下的麦穗都是同一个分布

  检验：看看在此假设下,$\overline{x}=130$发生的概率高不高。

  已知的数据是，A工艺下的单株麦穗的个数服从$\mu =100$，标准差$\sigma$未知的正态分布：

$X\sim N(\mu ,{\sigma }^2)$

  而B工艺下的麦田的样本均值$\overline{x}=120$，采样了5株。

  不同的标准差对应的正态分布图像不同：

  图像的跨度由标准差$\sigma$决定：

  X如果服从以下正态分布：

$X\sim N(\mu ,2)$

  ${\sigma }^2=2$，跨度不大，采样五个点使其$\overline{x}=120$的图像如下：

  可见，$\overline{x}=120$的概率非常低，即AB下的麦穗是同一个分布的可能性不大，我们有很大把握可以认为B工艺真正提高了产量。

  而如果X服从的是跨度更大的正态分布，采样五个点使其$\overline{x}=120$的图像如下（为了演示，正态分布的参数选的不是很严谨）：

  这样的正态分布下，$\overline{x}=120$的概率并不低，即AB下的麦穗还是可能为同一个分布的，我们没十足的把握认为B工艺提高了产量。

  因此，看起来不能单纯依靠$\overline{x}-{\mu }_0$，或许除以样本标准差 可以消除跨度的影响：

$\frac{\overline{x}-{\mu }_0}{s}$

  因为A工艺的$\sigma$我们不清楚，但是我们假设AB同分布，所以直接使用了样本标准差s。

  当然，样本数n也会影响结果。比如说，在n=1000下，得到$\overline{x}=120$，那么根据大数定理，我们不用算了，基本上可以认为“B工艺提高了产量”。

  所以，戈斯特认为应该综合考虑样本均值$\overline{x}$、样本方差s和样本数n，给出了一个统计量t值：

$t=\frac{\overline{x}-{\mu }_0}{s/\sqrt{n}}$

  该统计量越大说明AB工艺导致的差别越大，越有可能说明“B工艺提高了产量”。

3. t分布

  对于t值：

$t=\frac{\overline{x}-{\mu }_0}{s/\sqrt{n}}$

  对应的概率密度函数，也就是t分布为：

$f(t)=\frac{\Gamma ((v+1)/2)}{\sqrt{v\pi }\Gamma (v/2)}(1+t^2/v{)}^{-(v+1)/2}$

  其中v=n-1,也叫做自由度。而$\Gamma$为伽马函数。

  $f(t)$接近于正态分布$N(0,1)$(灰色虚线就是$N(0,1)$)下面是$v=2$的t分布:

  而t值，实际上对应的就是横坐标的值，比如说t值等于4：

  t=4之后的曲线下面积其实就是P值

  所以，我们知道t值之后，就可以根据$v=n-1$以及要求的P值，查出当前的t值是否会拒绝我们的假设。

  举个例子，比如本文中的AB工艺下的数据为：

$\mu =5$, $n=5$,$\overline{x}=120$ , $s=5\sqrt{5}$

  计算出来

$t=\frac{\overline{x}-{\mu }_0}{s/\sqrt{n}}=\frac{120-100}{5\sqrt{5}/\sqrt{5}}=4$

  服从$v=n-1=4$的t分布：

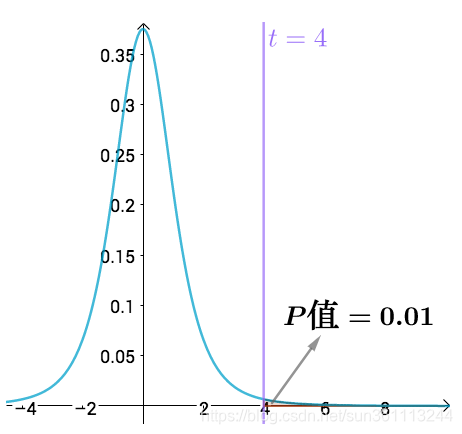
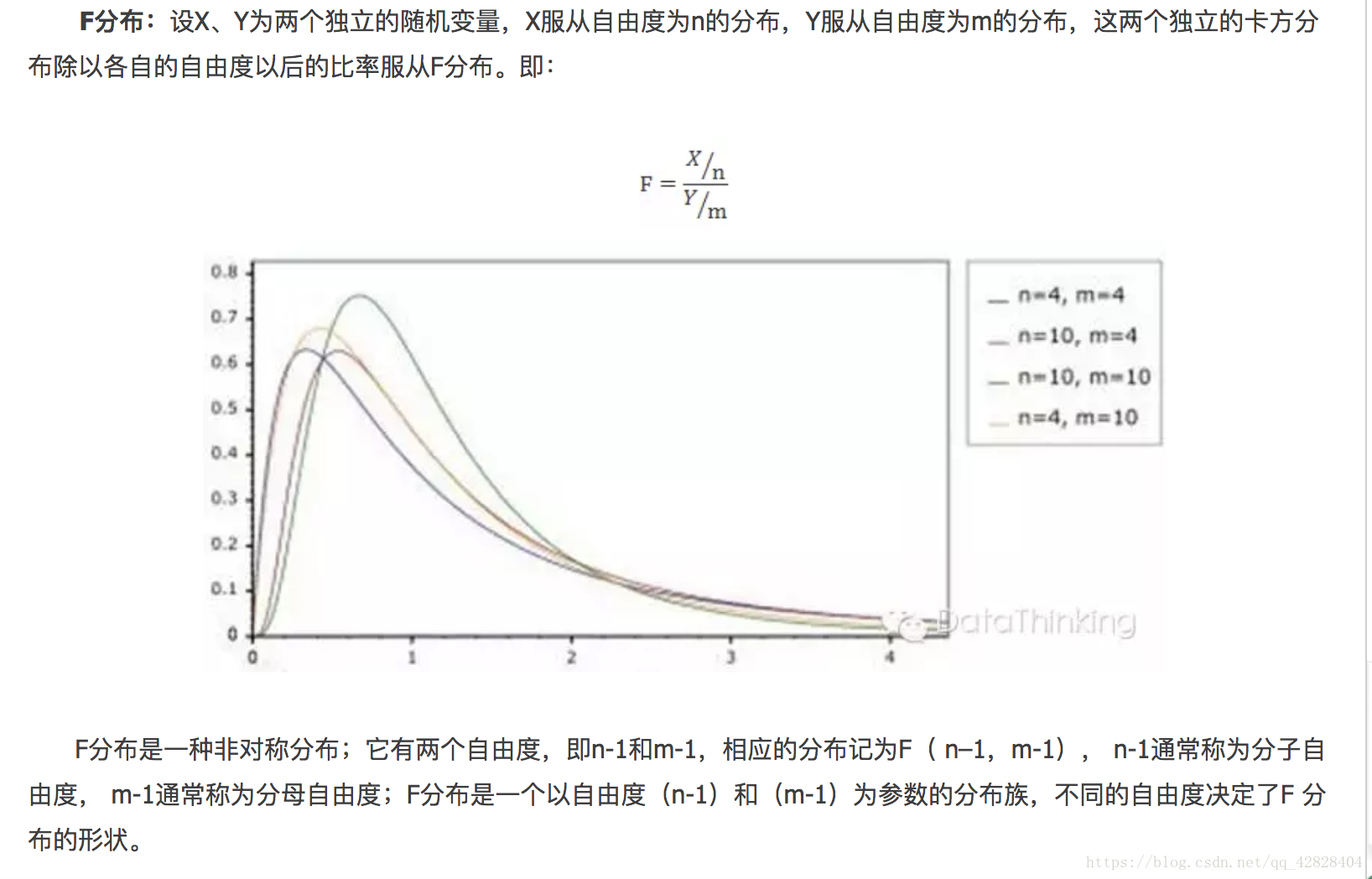
  如果我们要求5%的显著水平的话，那么就可以拒绝“B工艺没有提高产量”这个假设了。