TCP Nagle算法及示例

article/2025/7/23 4:51:32

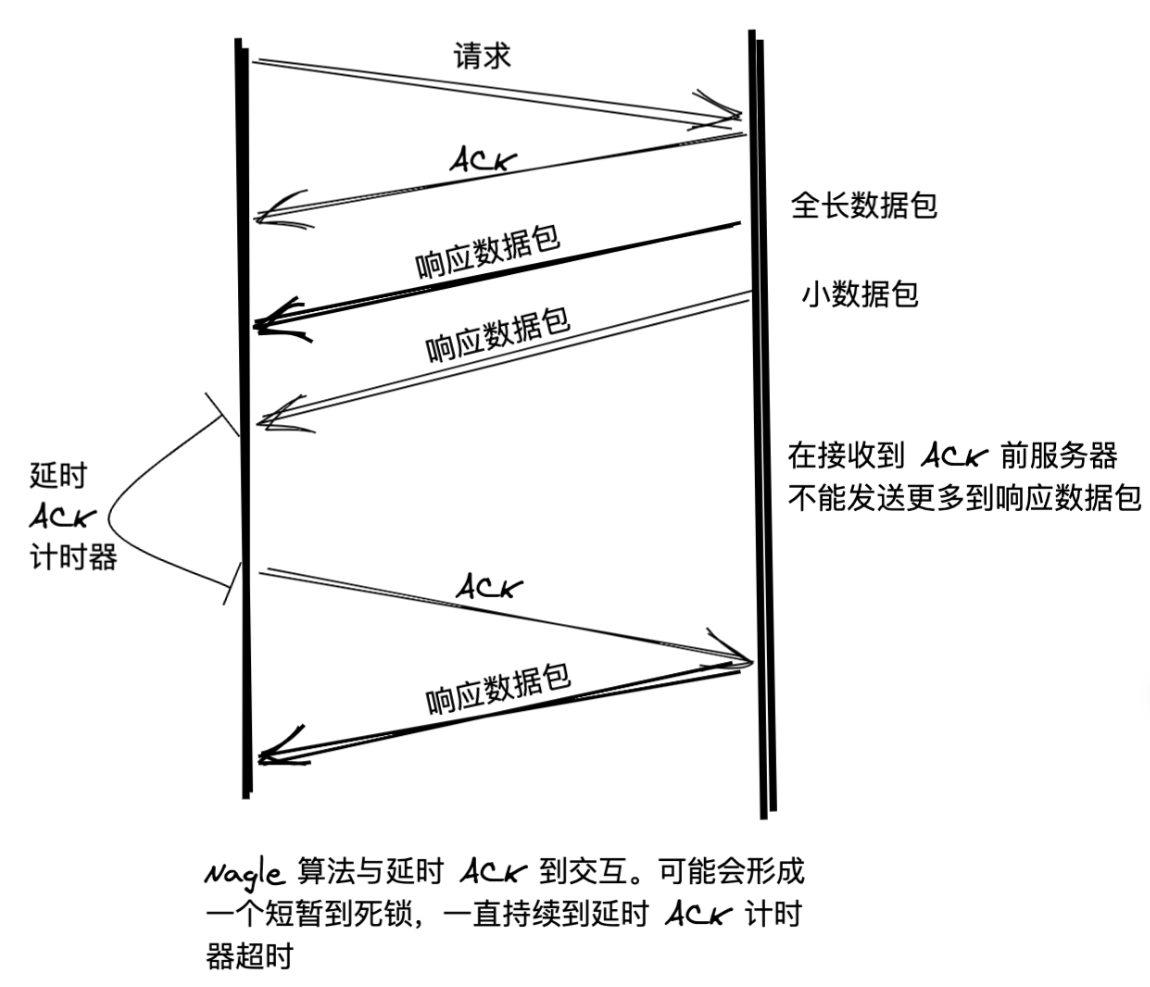
TCP nagle算法是说，一个TCP连接只允许有一个未被确认的小数据包，如果有小数据包未被确认，其他要发送的小数据包先被缓存起来，等收到确认后，把这些数据包再一块发送出去。注意算法中说的是小数据包，也就是nagle算法是针对发送许多小数据包时的算法。为什么会有这个算法？因为我们知道TCP头部一般就有20字节的长度，如果每次我只发送1字节的数据，那一个数据包的有效载荷只有1/21，所以，为了更高效发送数据，TCP设计了nagle算法，把小包收集起来一块发送。这个算法的精妙之处在于，如果我ack收到的越快，发送数据越快，如果ack收到的慢，说明网络环境不好，TCP发送数据也就越慢，这样就避免了给网络带来负担。

示例

首先我在本机windows电脑用netassist开启了1234端口，作为服务端。

然后编写如下代码，在一台centos虚拟机中执行，在执行之前，开启wireshark抓包。

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <arpa/inet.h>
#include <sys/socket.h>
#include <netinet/tcp.h>
#include <string.h>// nagle算法示例
int main(){// 创建套接字int sock = socket(AF_INET, SOCK_STREAM, 0);//向服务器（特定的IP和端口）发起请求struct sockaddr_in serv_addr;memset(&serv_addr, 0, sizeof(serv_addr));  //每个字节都用0填充serv_addr.sin_family = AF_INET;  //使用IPv4地址serv_addr.sin_addr.s_addr = inet_addr("192.168.52.1");  //具体的IP地址serv_addr.sin_port = htons(1234);  //端口int res = connect(sock, (struct sockaddr*)&serv_addr, sizeof(serv_addr));if(res != 0) {printf("connect fail %d\n", res);return 0;}// 向服务端发送多个小数据包char s[] = "abc";for(int i=0; i<100; i++) {write(sock, s, strlen(s));}sleep(1);close(sock);return 0;
}

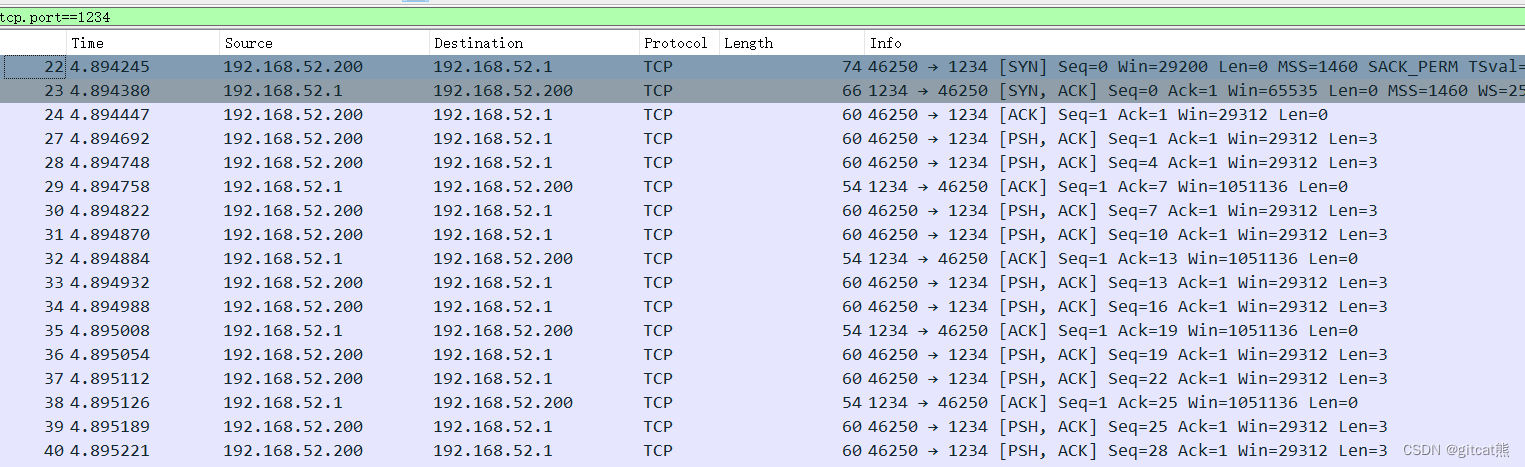
wireshark抓包内容如下：

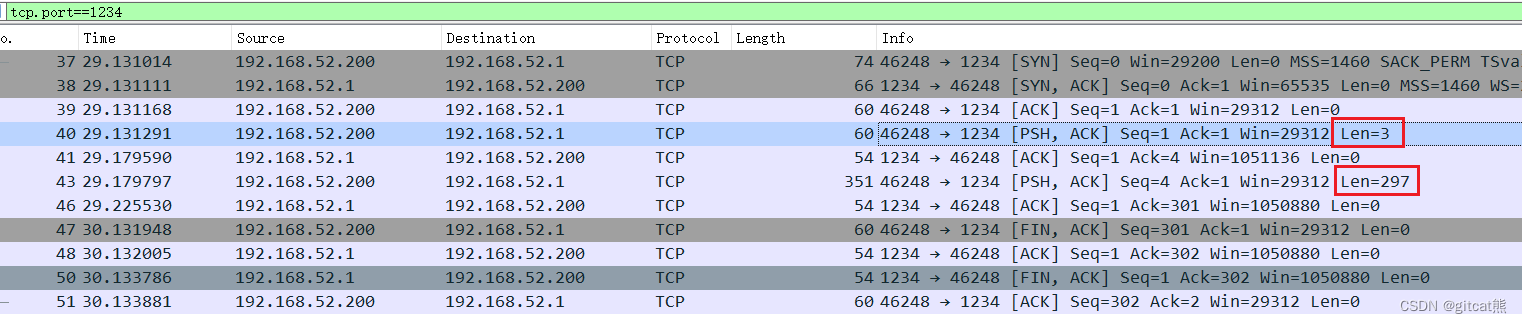
可以看到，第四行，tcp先发送了"abc"三个字节，然后就没有继续再发送，而是等到服务端回复了ack之后，又发送了另外的99个"abc"（共297字节）。说明nagle算法起作用了。

tcp提供了一种方式来关闭nagle算法，我们把nagle算法关闭，再来看效果。

修改上面的代码，改成如下：

#include <stdio.h>
#include <stdlib.h>
#include <unistd.h>
#include <arpa/inet.h>
#include <sys/socket.h>
#include <netinet/tcp.h>
#include <string.h>// nagle算法示例
int main(){// 创建套接字int sock = socket(AF_INET, SOCK_STREAM, 0);// 设置关闭nagle算法int setFlags = 1;socklen_t setFlagsLen = sizeof(setFlags);int setRes = setsockopt(sock, IPPROTO_TCP, TCP_NODELAY, &setFlags, setFlagsLen);printf("set nagle no delay flags result: %d\n", setRes);//向服务器（特定的IP和端口）发起请求struct sockaddr_in serv_addr;memset(&serv_addr, 0, sizeof(serv_addr));  //每个字节都用0填充serv_addr.sin_family = AF_INET;  //使用IPv4地址serv_addr.sin_addr.s_addr = inet_addr("192.168.52.1");  //具体的IP地址serv_addr.sin_port = htons(1234);  //端口int res = connect(sock, (struct sockaddr*)&serv_addr, sizeof(serv_addr));if(res != 0) {printf("connect fail %d\n", res);return 0;}// 向服务端发送多个小数据包char s[] = "abc";for(int i=0; i<100; i++) {write(sock, s, strlen(s));}sleep(1);close(sock);return 0;
}

此时我们再抓包看，如下，这里只截取了一部分，因为数据包太多了。可以看到tcp把我们在for循环中发送的"abc"一个个发送的，不再一块发送，也不再等待服务端ack之后再发送。