三角函数的正交性
- 三角函数的正交性
- 三角函数系
- 证明
三角函数的正交性
三角函数系
集合 { s i n 0 x , c o s 0 x , s i n x , c o s x , s i n 2 x , c o s 2 x , . . . } \lbrace sin0x, cos0x, sinx,cosx,sin2x,cos2x,... \rbrace {sin0x,cos0x,sinx,cosx,sin2x,cos2x,...}
正交
∫ − π π s i n n x c o s m x d x = 0 \int_{-\pi}^{\pi} sin\;nx\;cos\;mx\;dx=0 ∫−ππsinnxcosmxdx=0
∫ − π π c o s n x c o s m x d x = 0 n ≠ m \int_{-\pi}^{\pi} cos\;nx\;cos\;mx\;dx=0 \quad n \not= m ∫−ππcosnxcosmxdx=0n=m
正交意味着垂直
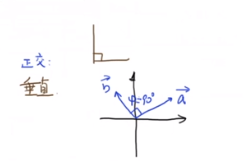
a ⃗ ⋅ b ⃗ = ∣ a ⃗ ∣ ∣ b ⃗ ∣ c o s φ \vec{a} \cdot \vec{b} = \mid \vec{a}\mid \mid \vec{b} \mid cos \varphi a⋅b=∣a∣∣b∣cosφ
当 a ⃗ \vec{a} a与 b ⃗ \vec{b} b垂直的时候, c o s φ = 0 cos \varphi = 0 cosφ=0
a ⃗ ⋅ b ⃗ = 0 \vec{a} \cdot \vec{b}=0 a⋅b=0
举例:
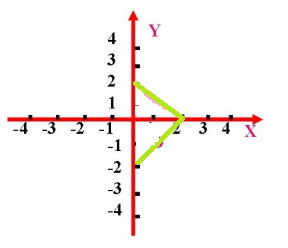
a ⃗ = ( 2 , 1 ) b ⃗ = ( − 1 , 2 ) \vec{a}=(2,1) \quad \vec{b}=(-1,2) a=(2,1)b=(−1,2)
a ⃗ ⋅ b ⃗ = ( 2 , 1 ) ⋅ ( − 1 , 2 ) = 2 ∗ − 1 + 1 ∗ 2 = 0 \vec{a} \cdot \vec{b}=(2,1) \cdot (-1,2) = 2*-1 + 1* 2 = 0 a⋅b=(2,1)⋅(−1,2)=2∗−1+1∗2=0
扩展:
a ⃗ = ( a 1 , a 2 , a 3 , . . . a n ) \vec{a}=(a_1,a_2,a_3,...a_n) a=(a1,a2,a3,...an)
b ⃗ = ( b 1 , b 2 , b 3 , . . . b n ) \vec{b}=(b_1,b_2,b_3,...b_n) b=(b1,b2,b3,...bn)
a ⃗ ⋅ b ⃗ = a 1 b 1 + a 2 b 2 + . . . + a n b n = ∑ i = 1 n a i b i = 0 \vec{a} \cdot \vec{b}=a_1 b_1 + a_2 b_2 + ...+ a_n b_n = \sum_{i=1}^n a_i b_i = 0 a⋅b=a1b1+a2b2+...+anbn=∑i=1naibi=0
进一步扩展:
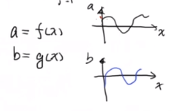
a = f ( x ) a=f(x) a=f(x)
b = g ( x ) b=g(x) b=g(x)
a ⋅ b = ∫ x 0 x 1 f ( x ) g ( x ) d x = 0 a \cdot b = \int_{x_0}^{x_1}f(x)g(x) dx =0 a⋅b=∫x0x1f(x)g(x)dx=0
当两个函数积分等于0的时候,我们说这两个函数正交。
证明
已知:
s i n ( A + B ) = s i n A c o s B + c o s A s i n B sin(A+B)=sinAcosB+cosAsinB sin(A+B)=sinAcosB+cosAsinB
s i n ( A − B ) = s i n A c o s B − c o s A s i n B sin(A-B)=sinAcosB-cosAsinB sin(A−B)=sinAcosB−cosAsinB
c o s ( A + B ) = c o s A c o s B − s i n A s i n B cos(A+B)=cosAcosB-sinAsinB cos(A+B)=cosAcosB−sinAsinB
c o s ( A − B ) = c o s A c o s B + s i n A s i n B cos(A-B)=cosAcosB+sinAsinB cos(A−B)=cosAcosB+sinAsinB
∫ − π π s i n n x c o s m x d x = ∫ − π π 1 2 [ s i n ( n − m ) x + s i n ( n + m ) x ] d x = 1 2 [ ∫ − π π s i n ( n − m ) x d x + ∫ − π π s i n ( n + m ) x d x ] = 1 2 [ − 1 n − m c o s ( n − m ) x ∣ − π π − 1 n + m c o s ( n + m ) x ∣ − π π ] = 0 + 0 = 0 \begin{aligned} \int_{-\pi}^{\pi} sinnx\;cosmx\;dx &= \int_{-\pi}^{\pi} \frac{1}{2}[sin(n-m)x+sin(n+m)x]dx \\ &= \frac{1}{2}[\int_{-\pi}^{\pi}sin(n-m)x \;dx+\int_{-\pi}^{\pi}sin(n+m)x \;dx] \\ &=\frac{1}{2}[-\frac{1}{n-m}cos(n-m)x \mid_{-\pi}^{\pi}-\frac{1}{n+m}cos(n+m)x \mid_{-\pi}^{\pi}] \\ &=0+0 \\ &=0 \end{aligned} ∫−ππsinnxcosmxdx=∫−ππ21[sin(n−m)x+sin(n+m)x]dx=21[∫−ππsin(n−m)xdx+∫−ππsin(n+m)xdx]=21[−n−m1cos(n−m)x∣−ππ−n+m1cos(n+m)x∣−ππ]=0+0=0
∫ − π π c o s n x c o s m x d x = ∫ − π π 1 2 [ c o s ( n − m ) x + c o s ( n + m ) x ] d x = 1 2 [ ∫ − π π c o s ( n − m ) x d x + ∫ − π π c o s ( n + m ) x d x ] = 1 2 [ 1 n − m s i n ( n − m ) x ∣ − π π + 1 n + m s i n ( n + m ) x ∣ − π π ] = 0 + 0 = 0 \begin{aligned} \int_{-\pi}^{\pi} cosnx\;cosmx\;dx &= \int_{-\pi}^{\pi} \frac{1}{2}[cos(n-m)x+cos(n+m)x]dx \\ &= \frac{1}{2}[\int_{-\pi}^{\pi}cos(n-m)x \;dx+\int_{-\pi}^{\pi}cos(n+m)x \;dx] \\ &=\frac{1}{2}[\frac{1}{n-m}sin(n-m)x \mid_{-\pi}^{\pi}+\frac{1}{n+m}sin(n+m)x \mid_{-\pi}^{\pi}] \\ &=0+0 \\ &=0 \end{aligned} ∫−ππcosnxcosmxdx=∫−ππ21[cos(n−m)x+cos(n+m)x]dx=21[∫−ππcos(n−m)xdx+∫−ππcos(n+m)xdx]=21[n−m1sin(n−m)x∣−ππ+n+m1sin(n+m)x∣−ππ]=0+0=0
当 m = n m= n m=n 时
∫ − π π c o s m x c o s m x d x = ∫ − π π 1 2 [ 1 + c o s 2 m x ] d x = 1 2 [ ∫ − π π 1 d x + ∫ − π π c o s 2 m x d x ] = 1 2 [ ∫ − π π 1 d x + 0 = 1 2 x ∣ − π π = π \begin{aligned} \int_{-\pi}^{\pi} cosmx\;cosmx\;dx &= \int_{-\pi}^{\pi} \frac{1}{2} [1+cos2mx]dx \\ &=\frac{1}{2}[ \int_{-\pi}^{\pi} 1 dx+ \int_{-\pi}^{\pi}cos2mx dx] \\ &=\frac{1}{2}[ \int_{-\pi}^{\pi} 1 dx+0\\ &=\frac{1}{2}x \mid_{-\pi}^{\pi} \\ &=\pi \end{aligned} ∫−ππcosmxcosmxdx=∫−ππ21[1+cos2mx]dx=21[∫−ππ1dx+∫−ππcos2mxdx]=21[∫−ππ1dx+0=21x∣−ππ=π
原视频:
https://www.bilibili.com/video/av34364399/?spm_id_from=333.788.videocard.1