文章目录
- 背景
- Nagle算法详解
- 算法实现
- 实现
- 开启与关闭Nagle算法
- Nagle算法与延迟ACK
- 参考
背景
TCP的数据流大致可以被分成两类：
-
交互式数据流
TCP交互数据流指的是：TCP连接中传输的所有数据的总和，包括
控制命令（用于管理网络中连接，传输数据和处理错误，如telnet的send和put命令）和应用程序的数据。 -
成块数据流
成块数据流是用来发送数据的包，网络上大部分都是这种包。TCP中，数据被分成了一个一个的TCP数据包进行传输，
成块数据包指的是，在上层应用视角，TCP提供了一个连续无间断的数据流。
TCP在传输这两种数据包时的效率不同。为了提高TCP效率，需要对这两种包采用不同的算法。其中的原则是：尽量减少小分组传输的数量。
Nagle算法详解
在TCP连接中，任意时刻只能有一个未被确认的小片段。在发送出去的报文中，必须要等待对方发送ACK之后，服务端才会发送一个新的报文。
Nagle算法的主要目的是为了预防小分组的产生，因为在广域网中，小分组会造成网络拥塞。
当网络中存在大量小分组时，网络拥塞出现的可能性会增加，因为每个小分组都需要占据
网络带宽和路由器缓存空间。由于TCP要求每个小分组发送之前都需要进行确认，分组数量过多会导致消息数量增多，从而导致确认消息的数量增加，进而导致网络延迟和吞吐量下降。
Nagle算法的原理：
Nagle要求一个TCP连接上最多只能有一个未被确认的小分组。这意味着，在发送完一个小分组后，需要一直等待该分组的确认ACK到达，否则不会发送其他的分组。当确认到达之后，TCP会收集已经准备好的小分组，并将它们合并成一个大的分组发送出去，从而减少了
网络拥塞的可能性，降低了网络延迟，并提高了吞吐量。
缺点
- 严重影响请求响应式协议的延迟（例如Redis中是把Nagle算法禁止掉的，避免延迟,因为Redis的命令都要求尽快的传输到Redis服务器，而不需要等待其他命令或缓冲区填充）
- 对于实时性要求很高的交互上，我们也禁止使用Nagle
算法实现
Nagle算法的实现是通过下面的伪代码表述的：
if 有数据要发送:
{if 可用窗口大小>=MSS and 可发送数据>=MSS:立即发送MSS大小的数据else:if 有未确认的数据:将数据放入缓存等待ack
}
else:立即发送数据
具体来说，Nagle算法的实现原理和过程是这样的：
- 接收到了客户端发送过来的ACK。
- 如果包长度达到了
MSS(1460)，则允许发送。 - 如果该数据包含有
FIN，则允许发送。 - 如果设置了
TCP_NODELAY，则允许发送。 - 如果达到了
超时时长(200ms)，则允许发送。 - 如果未设置
TCP_CORK，且所有已发出去的小数据包的个数超过了最大值，默认是200个，则允许发送。
该算法的精妙之处在于实现了一个自时钟控制。ACK返回得越快，数据传输就越快，这使得在单位时间内发送的报文更少。
实现
//Go 模拟实现Nagle算法
/*实现Nagle算法的核心就是在发送数据的时候进行缓存和延迟*/
package mainimport ("net""sync""time"
)//这里使用互斥锁来保证线程安全
var mu sync.Mutexfunc main() {//conn变量代表与服务段的TCP连接，这个是一个客户端conn, err := net.Dial("tcp", "localhost:8080")if err != nil {panic(err)}//用于在函数执行完之后，自动断开连接defer conn.Close()//模拟Nagle算法：缓存小的数据包，在一定事件或者缓存到一定程度的时候发送//sendbuffer只哦叛逆用来缓冲需要发送的小数据包，等待合并sendBuffer := make([]byte, 0) //创建一个空的字节片,长度为0,可以将空的字节片看作一个缓冲区，在需要的时候进行动态扩容maxSendBufferSize := 1024 //需要缓存的最大容量delayedSecond := time.Second //发送的延迟时间,发送小数据包等待的最大时间lastSendTime := time.Now() //当前时间//向服务器发送数据msg1 := "hello"msg2 := "world"//将数据缓存到,//将byte数据一个字节一个字节添加到sendBuffer中sendBuffer = append(sendBuffer, []byte(msg1)...)sendBuffer = append(sendBuffer, []byte(msg2)...)for {mu.Lock()if len(sendBuffer) > 0 {idleSecond := time.Since(lastSendTime) //计算距离上一次有多少时间//如果当前缓存的数据量达到了指定的发送大小或者时间已经达到了超时时间。就需要发送if len(sendBuffer) >= maxSendBufferSize || (idleSecond >= delayedSecond && len(sendBuffer) > 0) {n, err := conn.Write(sendBuffer)if err != nil || n == 0 {panic(err)}lastSendTime = time.Now()//因为已经成功发送了n个字节，所以就需要从n位置开始截取新的切片，进行下一次的发送sendBuffer = sendBuffer[n:] //这个截取一个切片}}mu.Unlock()}
}
开启与关闭Nagle算法
当chOPt=1时关闭Nagle算法,不用等待ACK可以连续的发送
当chOpt=0时打开Nagle算法
int nErr=setsockopt( m_socket, IPPROTO_TCP, TCP_NODELAY, &chOpt, sizeof(char));
Nagle算法与延迟ACK
延迟ACK指接收端等待延时ACK计时器后统一对接收到的报文进行ACK，而非每个报文都立即ACK。
Nagle算法指规定一段时间内，只有一个报文会在传输，等待缓冲区满或者收到ACK才会发送新报文。
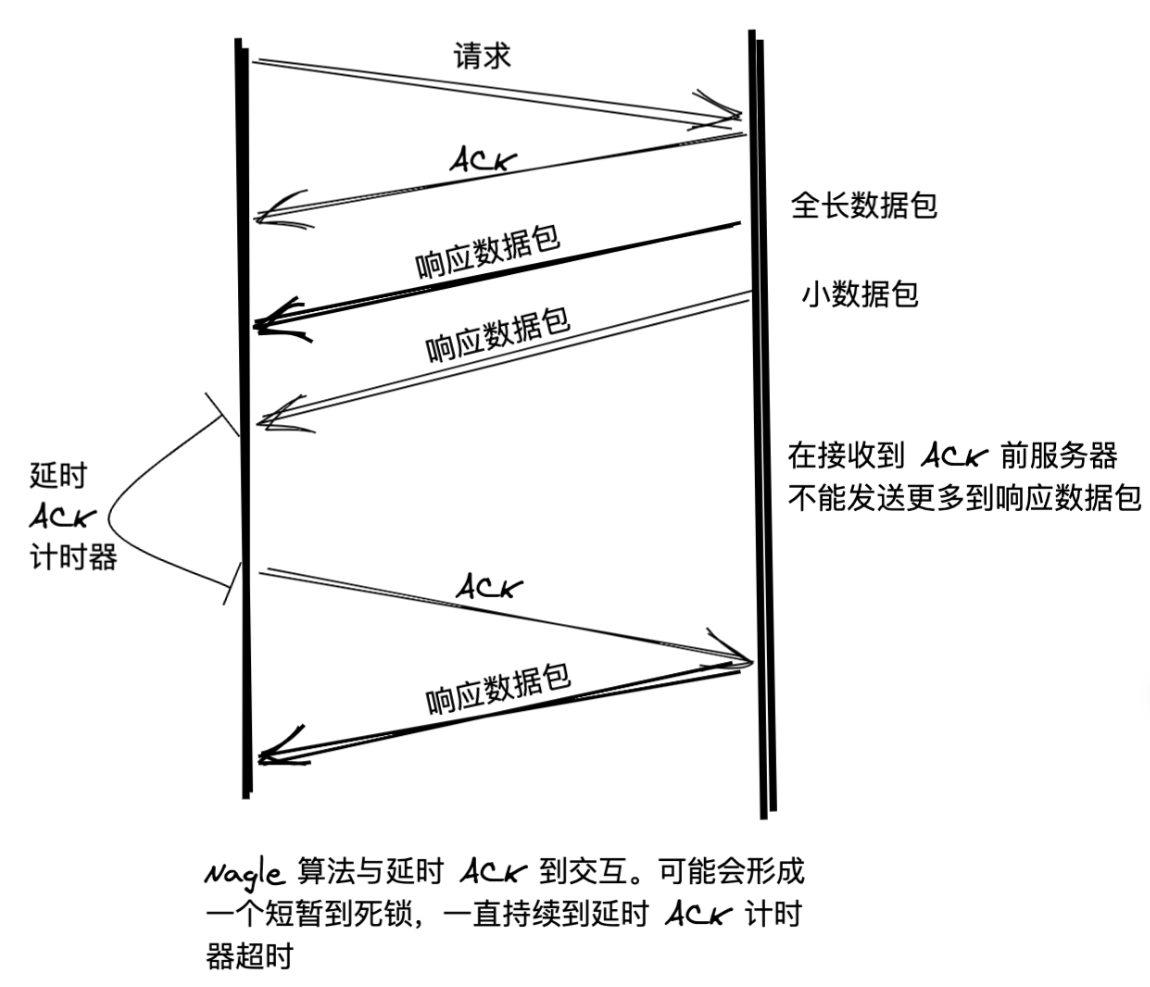当客户端（client）发送消息给服务器（server）时，若客户端收到ACK后等待延时ACK计时器结束才进行延迟应答，服务器由于未收到对方的ACK而一直等待，可导致死锁，此时只有等待延时计时器结束（至少40ms）才能解决死锁问题。
write-write-read模式对服务器而言也会造成类似的延迟问题，例如在需要发送两个报文 A、B的情况下，使用此模式时发送 A 报文后，服务器会等待客户端发送 A 报文的ACK，但如果客户端延迟响应，导致过了一段时间才发送ACK，才会发送 B 报文。这会极大增加延迟。
针对此问题，有两种解决方案：
- 将两个
write合并，变成一个write-read的过程，从而避免使用Nagle算法导致的延迟问题。 - 禁用Nagle算法。
参考
深入浅出TCPIP之Nagle算法
【TCP/IP】Nagle 算法以及所谓 TCP 粘包
TCP之Nagle算法和延迟确认及关闭参数
【网络编程实践】2.3.4.2 建议关闭 Nagle 算法
【1】TCP/IP 详解 卷1:协议
