目录

一.问题

二.安装说明

一、在一个盘符下新建一个目录

二、双击oracle的安装包开始安装。

三、最后安装完成，桌面会有一个oracle主页的快捷键，这个并没有什么重要，删掉即可！

四、如何测试oracle是否安装成功呢？

---

一.问题

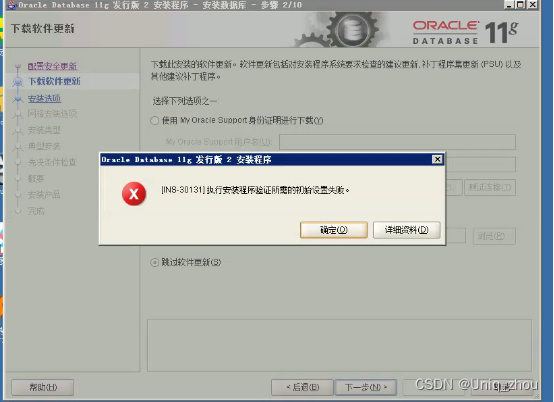
问题：在安装oracle的时候出现了一个弹出框里面的乱码提示

 解决办法：可能是因为你的安装路径带特殊字符(尽量纯英文路径)

注意事项：

1.先查看jdk是否存在

查看命令：

 java  -version

2.JDK环境变量顺序在要在Oracle环境变量顺序的前面

二.安装说明

一、在一个盘符下新建一个目录

（注意：这个目录不能包含中文以及特殊符号，只能是英文）

二、双击oracle的安装包开始安装。

安装时选择安装目录，安装到刚才新建的文件夹中。

在安装过程中，有一个界面需要你输入口令，

注意：这个口令是连接oracle的密码，一定要记住，

为了避免以后会忘记，最好设置简单点的密码

三、最后安装完成，桌面会有一个oracle主页的快捷键，这个并没有什么重要，删掉即可！

四、如何测试oracle是否安装成功呢？

1、打开cmd命令终端

2、在终端中输入“sqlplus”

3、输入用户名（用户名为默认的SYSTEM，注意：这个是大写）

4、输入密码（也就是在第二步中你自己设置的口令）

5、如果出现 SQL> ，恭喜你，安装成功！

6、下面我们就可以在终端里写sql语句了

如果在终端里写sql语句看着不舒服，那么我们就可以用sqldeveloper工具来解决。

1、直接解压sqldeveloper.zip

2、找到里面的sqldeveloper.exe快捷键

3、双击打开

4、进行连接配置

        连接名： 这个随便写，只是一个名字

        用户名： 默认是SYSTEM

        口 令： 你自己设置的密码

        主机名： localhost（或者本机具体的IP，例如我的是192.168.221.138）

        端 口： 1521（一般oracle的端口都是1521）

        SID： XE（通常oracle的SID是orcl或者xe，如果这两个都不行，那就是在安装的时候把SID改了）

5、点击“测试”，如果显示成功，就连接，出现错误的话就看一下错误信息。

最后记住，sqldeveloper跟oracle没有关系，它只是连接oracle服务的一个工具（图形化界面），没有sqldeveloper也可以在cmd命令行里写sql语句。