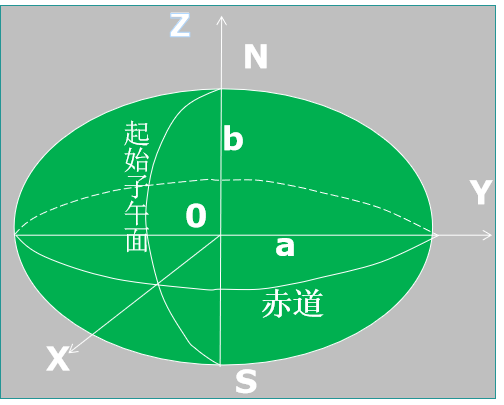
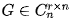闫令琪图形学入门笔记（矩阵变换篇）

整个坐标变化过程贯穿管线渲染，它与光栅化、着色一同构成GPU完整的渲染过程。所以理解三维世界的坐标与矩阵变换是首要的学习内容
在这里插入图片描述

1.1 向量的点乘与叉乘

点乘

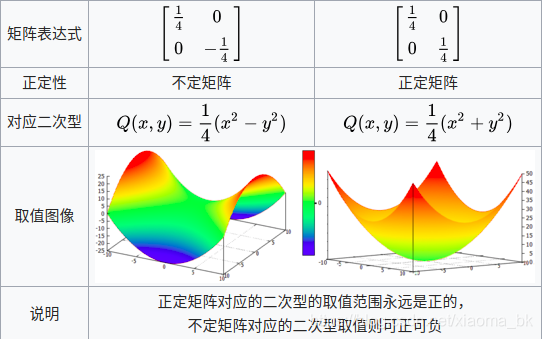
向量的点乘可以求得一个数，利用点乘可以进一步计算两向量的夹角大小，或者一个向量在另一向量的投影长度。这一运算可用于路径判断中

叉乘

叉乘的含义决定，计算结果是一个向量。结果向量方向上垂直于参加叉乘的两向量，因此称之为法向量，根据右手螺旋定则（先将两向量移动到同一起点，右手四指从a转到b,则拇指所指方向，即为结果向量的方向）确认计算结果的方向，将多边形各边与某一点向量依次做叉乘，可以判断某点是否位于多边形内部，这在光栅化中极为重要。
在这里插入图片描述

1.2 左乘矩阵

矩阵描述的是运动，是线性变换，向量左乘矩阵即代表该向量进行某种线性变换后产生新的向量。当然只有线性变化不足以表示图形学中的所有图像操作，因此可大致分为以下几种矩阵变换

1.2.1 线性变换

线性代数限制在一种特殊类型的变换上，即线性变换。如果一个变换拥有以下两个性质，我们就称它为线性的变化：

直线在变换后仍保持直线，不能有所弯曲。
原点保持固定

我们熟知的线性矩阵变化包括

缩放
$\begin{bmatrix} s & 0 \\ 0 & s \end{bmatrix} \quad * \begin{bmatrix} x \\ y \end{bmatrix} = \quad \begin{bmatrix} s*y \\ s*x \end{bmatrix} \quad$
在这里插入图片描述

推移（切变）

$\begin{bmatrix} 1 & a \\ 0 & 1 \end{bmatrix}* \quad \begin{bmatrix} x \\ y \end{bmatrix} = \quad \begin{bmatrix} x+ay \\ y \end{bmatrix} \quad$
在这里插入图片描述

旋转
$\begin{bmatrix} cosθ & -sinθ \\ sinθ & cosθ \end{bmatrix}* \quad \begin{bmatrix} x \\ y \end{bmatrix} = \quad \begin{bmatrix} cosθ *x - sinθ*y \\ sinθ *x+cosθ*y \end{bmatrix} \quad$
在这里插入图片描述

1.2.2 平移与仿射变换

平移的矩阵表示与线性变换格格不入，涉及到了矩阵的加法，实际上平移不是线性变换
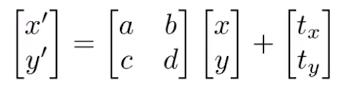
在这里插入图片描述

而仿射变换实际就是线性变换+平移，那么十分有必要将平移写成矩阵形式，为此引入齐次坐标

将向量维数加1，且新加一维的数值为0（根据向量的平移不变性，三维空间类推），就可以把平移用矩阵左乘写出来。同样线性变化也可以在齐次坐标下表示出来
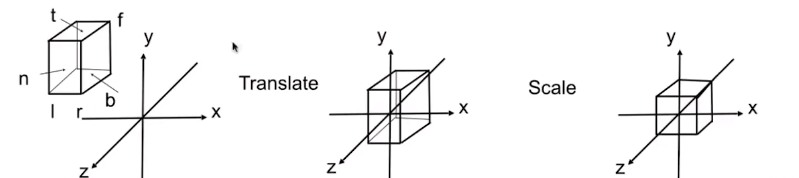
在这里插入图片描述
继续引出仿射变化，例如下图的转换

直接左乘旋转矩阵无法得到右图，因为旋转是绕原点进行的，所以需要经过先旋转后平移（变换的复合）实现：

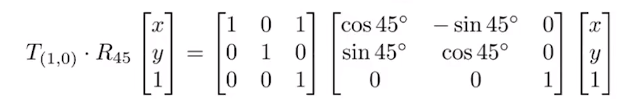
这里有两点注意：

平移后再旋转已经构成个仿射变换
矩阵变换的顺序不可调换，否则影响最终结果

1.2.3 投影变换（正交投影与透视投影）

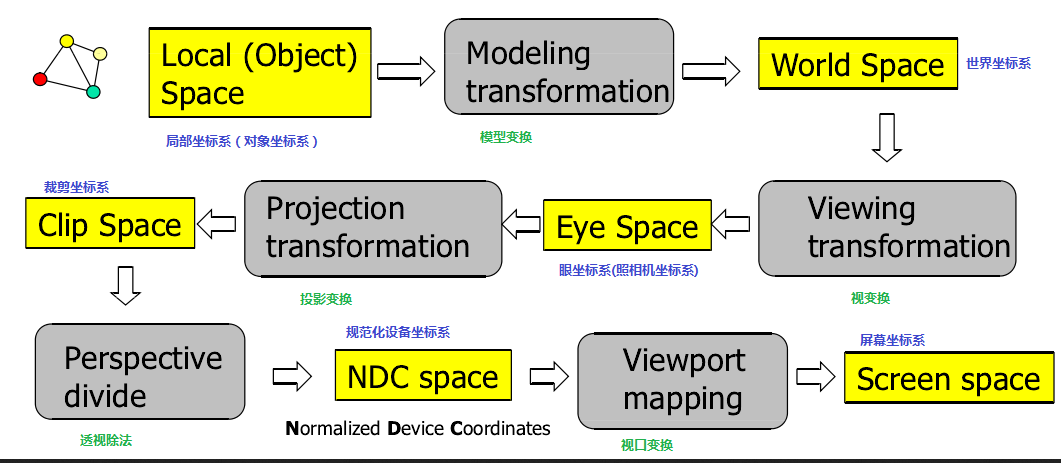
三维图形从制作到显示到屏幕上需要经历MVP+视口变换四个步骤

M 模型变换：即将计算机世界中的物体模型放置到规定的世界坐标系位置中，对应OpenGL中的world space
V视图变换：调整摄像机的位置、方向以及摄像机的向上调整最终将其放到世界坐标系的原点（实际按照相对运动原理，一切关于摄像机的移动同时作用在物体之上，就可以确保两者相对位置的固定），对应OpenGL中的eye/camera space
P 投影变换：包括正交投影与透视投影，他们的最终目的都是把复杂的三维图形”挤压“到一个立方体中，而最终成像（光栅化）时从立方体的一个面看过去都是一张标准的二维图（其中深度信息会用于遮挡检测）。
透视变换具有近大远小的特点，更符合人眼对于三维物体的平面成像。透视投影其实是分成两步：首先将视锥体挤压成长方体，再做一次正交投影得到最终的立方体，对应OpenGL中的eye/camera space。具体步骤下面会展开来看

OpenGL中的还有一个透视除法，得到归一化设备坐标，即NDC space

视口变换：上一步压缩会让最终得到的XY二维图的比例失调，且实际显示器的宽高比也是不同的，所以视口变换就是将二维图形的比例进行依次转换而已. 对应OpenGL中的screen space：
整个变换流程如下图：

重点来看投影变换的细节，以下内容可以认为是线性变换（不包括旋转）与平移在三维中的表示

正交投影
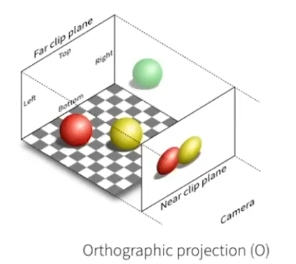
在这里插入图片描述
一般的正交变换并没有得到最终的二维图，而是将原先位于认为规定的长方体内的物体挤压到一个位于原点的立方体（所有轴的范围均位于-1 到1）中，因此正交投影只涉及平移与缩放

我们定义原长方体的尺寸如下：
在这里插入图片描述
根据推导可以得出最终的变换矩阵（缩放+平移）

透视投影

视锥体的远近平面包含了要显示的所有物体，摄像机相当于人眼，那么我们如何得到远大近小的效果呢？其实如果把远平面进行挤压，越靠近远平面的物体变小的越严重，那么相比来说越靠近近平面的物体就会变得更大，最终大小相等的两个物体会出现远大近小的效果。具体透视投影也分为两步

仅平面保持不变，缩小原平面

这一步的变换中，xy轴为缩放，很容易得出，而z轴需要依赖两个人为假设

Near clip plane上的任意点，设为(i,j,n)，它的z值不变依旧为 n。
Far clip plane上的任意点，设为(k,l,f)，它的z值不变依旧为 f。
常量k ！= 0，通过其次坐标我们可以知道，(x,y,z,1) 是等价于 (kx,ky,kz,k)
推导后得到挤压矩阵是（引入齐次坐标原因是z其实有向远平面的位移，必须使用齐次坐标来表示）

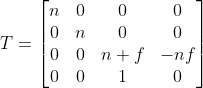
上式中，前两列代表xy轴的缩放，而第3、4列则是有上面三个假设得到
详细推导过程

1.3 其它矩阵性质

相似矩阵
一句话：相似的矩阵是同一个线性变换在不同基/坐标系下的的不同描述。
线性变换若粗略看成一个刚体的特定运动。刚体的特定运动是同一个，
但坐标系改变的话这个运动的描述函数就会不一样，如果这个函数可用矩阵等价替代的话，
一个坐标系就对应着一个矩阵，因此这些矩阵就不同，但这些矩阵必有关系，这个关系就是相似

1.3.1 正交矩阵

这种矩阵就是保持两点的欧式距离不变的线性变换，类似于把一个方方正正的立方体变成斜的

1.3.2 对称矩阵

对称矩阵定义的主要目的是因为它有一系列良好的性质。
比如对称矩阵如果可对角化，那么一定可被正交对角化。
几何上来看，这意味着对称矩阵的本征向量是正交的

1.3.3 正交对角化

正交矩阵是一个在三维坐标系中歪着摆的立方体。
对角化就是把这个立方体摆正来（也就是让它某一个顶点放在原点上，同时这个顶点的三条边正好对在三维坐标系的xyz三条轴上）
所以这个定理的意思就是，任何歪着摆的立方体劳资都能把它摆正了。这定理还是蛮直观的。

1.3.4 正定矩阵

对称的矩阵，而且是某个二次型方程的矩阵表示时的矩阵，二次型如果恒大于0，那么二次型为正定的，这个矩阵也是正定的
这个矩阵用在求二次型极值很有意义

1.3.5 矩阵的特征值与特征向量

矩阵是运动，是变换，那么矩阵的特征向量是就矩阵的各个变换方向，而特征值就是该变化的重要程度
方阵可以分解为相似矩阵与特征值矩阵的乘积，那么就很容易找到方阵的主要变化特征
马同学知乎

1.3.6 卷积

一个函数效果被另一函数翻转与平移（卷）后在一定时间内影响的叠加（积）结果
https://www.zhihu.com/question/22298352
https://blog.csdn.net/liuxiangxxl/article/details/84836164
https://blog.csdn.net/weixin_39124778/article/details/78411314
https://blog.csdn.net/kilotwo/article/details/88403079