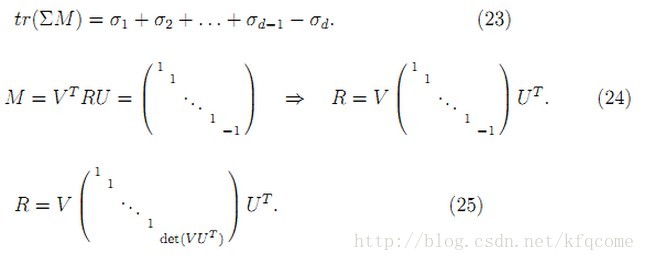原文地址：http://www.bfcat.com/index.PHP/2012/03/svd-tutorial/

SVD分解（奇异值分解），本应是本科生就掌握的方法，然而却经常被忽视。实际上，SVD分解不但很直观，而且极其有用。SVD分解提供了一种方法将一个矩阵拆分成简单的，并且有意义的几块。它的几何解释可以看做将一个空间进行旋转，尺度拉伸，再旋转三步过程。

首先来看一个对角矩阵，

几何上, 我们将一个矩阵理解为对于点  (x, y)  从一个平面到另一个平面的映射:

下图显示了这个映射的效果: 平面被横向拉伸了3倍，纵向没有变化。

对于另一个矩阵

它的效果是

这样一个变化并不是很好描述，然而当我们将坐标系旋转45度后，我们可以看出

这时，我们发现这个新的网格上发生的变化和网格在对角阵下发生变化的效果相似。

这是一个对称矩阵的例子，可以看出，对称矩阵经过旋转后，其作用就和对角阵类似了。数学上，对于一个对称矩阵 M, 我们可以找到一组正交向量 v_i 从而 Mv_i 相当于 v_i上的标量乘积; 也就是

M v_i = λ _i v_i λ _i  是标量，也就是对应对角阵中对角线上的元素. 由于这个性质，我们称  v_i  是  M  的特征向量; λ _i  为特征值 . 一个对称矩阵不同特征值对应的特征向量是正交的。

对于更广泛的情况，我们看看是否能从一个正交网格转换到另一个正交网格. 考虑一个非对称矩阵:

这个矩阵的效果形象的称为剃刀（ shear ）。

这个矩阵将网格在水平方向拉伸了，而垂直方向没有变化。如果我们将网格旋转大约58度，这两个网格就又会都变为正交的了。

奇异值分解：

考虑一个 2 *2 矩阵, 我们可以找到两组网格的对应关系。用向量表示，那就是当我们选择合适的单位正交向量 v₁ 和v₂, Mv₁ 和 Mv₂ 也是正交的.

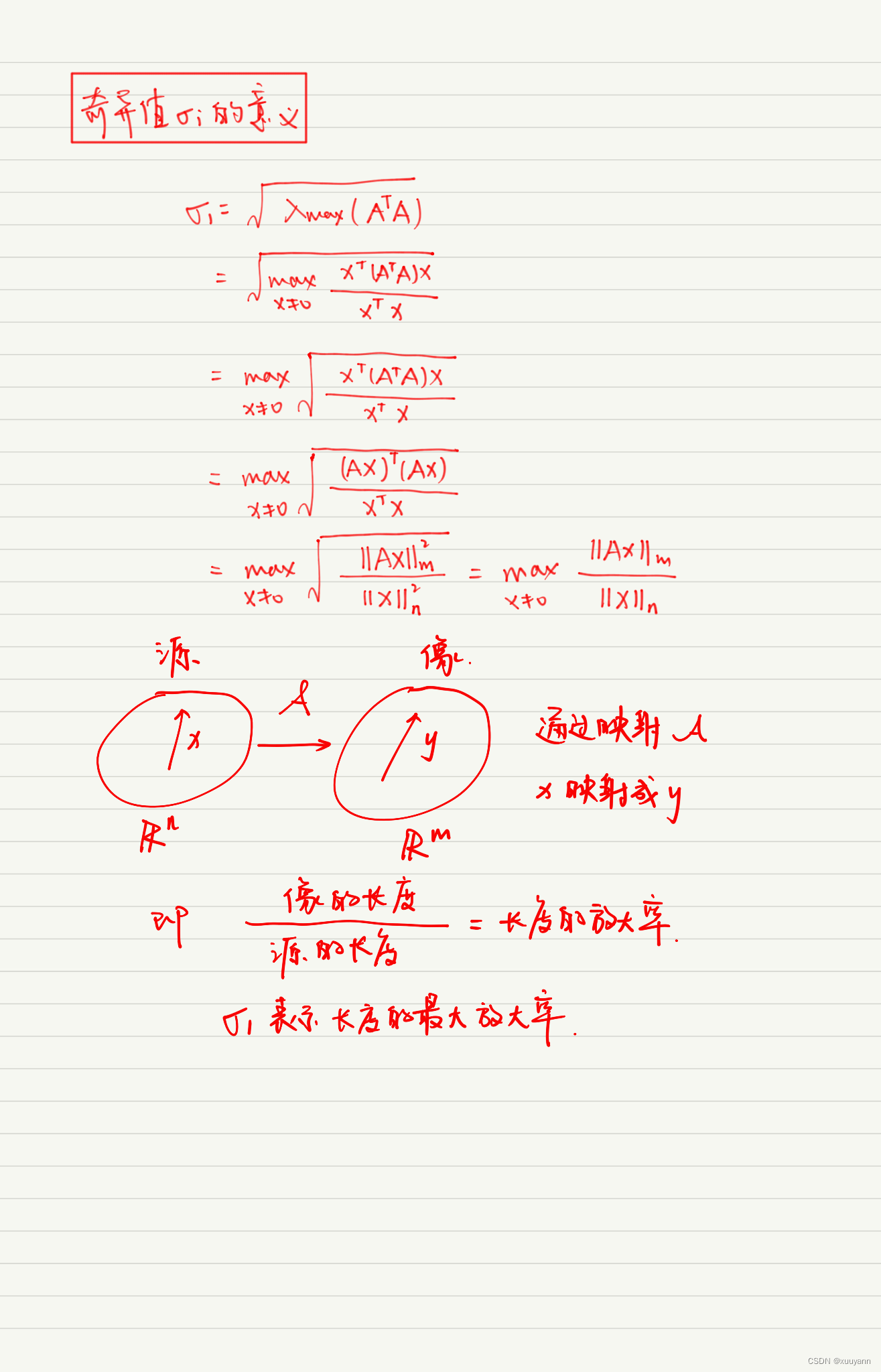
我们使用 u₁ 和 u₂ 代表 Mv₁ 和 Mv₂的方向. Mv₁ 和 Mv₂ 的长度表示为 σ₁ 和 σ₂，也就是网格在每个方向的拉伸.这两个拉伸值叫做M的 奇异值（sigular value）

和前面类似，我们可以 有

Mv₁ = σ₁u₁

Mv₂ = σ₂u₂

我们一直讨论的 v₁ 和 v₂ 是一对正交向量， 对于一般的向量 x，我们有这样的投影关系

x = ( v₁ x)  v₁ + ( v₂ x)  v₂ 也就是说

M x = ( v₁ x)  M v₁ + ( v₂ x)  M v₂ M x  = ( v₁ x ) σ ₁ u₁  + ( v₂x ) σ ₂ u

即

Mx = u₁σ₁ v₁^Tx + u₂σ₂ v₂^Tx ---> M = u₁σ₁ v₁^T + u₂σ₂ v₂^T

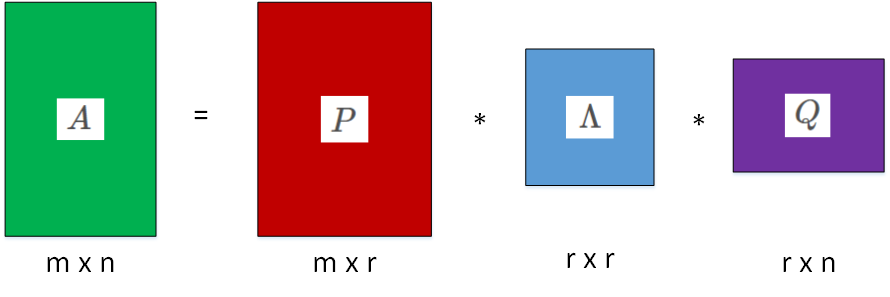
这个关系可以写成矩阵形式

M =  UΣ V^T U  的列是  u ₁  和  u ₂ , Σ σ ₁  和 σ ₂ 构成的对角阵,  V  的列是  v ₁  和  v ₂ . 即V描述了域中的一组正交基，U描述了相关域的另一组正交基，Σ 表述了U中的向量与V中向量的拉伸关系。

寻找奇异值分解

奇异值分解可以应用于任何矩阵，对于前面的例子，如果我们加上一个圆，那它会映射成一个椭圆，椭圆的长轴和短轴定义了新的域中的正交网格，可以被表示为Mv₁ and Mv₂。

换句话说，单位圆上的函数 |Mx| 在 v₁ 取得最大值，在 v₂取得最小值. 这将单位圆上的函数优化问题简化了。可以证明，这个函数的极值点就出现在M^TM的特征向量上，这个矩阵一定是对称的，所以不同特征值对应的特征向量v_i是正交的.

σ_i = |Mv_i|就是奇异值, u_i 是 Mv_i方向的单位向量.

M v_i = σ _i u_i M v_j = σ _j u_j. M v_i   M v_j =  v_i ^T M ^T  M v_j =  v_i   M ^T M v_j = λ _j v_i   v_j = 0. 也就是

M v_i   M v_j = σ _iσ _j  u_i   u_j = 0 因此,  u_i  和  u_j  也是正交的。所以我们就把一组正交基  v_i  变换到了另一组正交基  u_i .

另一个例子

我们来看一个奇异矩阵（秩为1，或只有一个非零奇异值）

它的效果如下

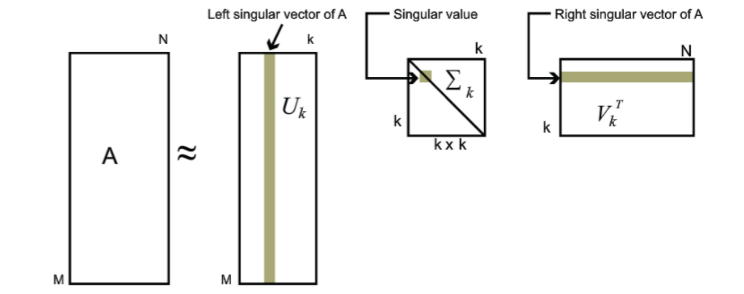
在这个例子中，第二个奇异值为0，所以 M = u₁σ₁ v₁^T. 也就是说，如果有奇异值为0，那么这个矩阵就有降维的效果。因为0奇异值对应的维度就不会出现在右边。这对于计算机科学中的数据压缩极其有用。例如我们想压缩下面的15  25 像素的黑白图像

我们可以看出这个图像中只有三种列，即

    把图像表示成一个15   25 的矩阵，总共有 375 个元素.

然而当我们做了奇异值分解，会发现非零奇异值仅有3个，

σ ₁ = 14.72， σ ₂ = 5.22， σ ₃ = 3.31 因此，这个矩阵就可以被表示为  M = u ₁ σ ₁   v ₁ ^T  +  u ₂ σ ₂   v ₂ ^T  +  u ₃ σ ₃   v ₃ ^T

也就是说我们用三个长度为15的向量v_i，三个长度为25的向量u_i，以及三个奇异值，总共123个数字表示了这个375个元素组成的矩阵。奇异值分解找到了矩阵中的冗余信息实现了降维。

可以看出，奇异值分解捕获了图像中的主要信息。因此，又假设上一个例子里引入了噪声，

当我们用同样的方法做奇异值分解，我们得到如下非零奇异值

σ ₁ = 14.15，σ ₂ = 4.67，σ ₃ = 3.00，σ ₄ = 0.21，σ ₅ = 0.19，...，σ ₁₅ = 0.05 显然，前三个奇异值比其他的大很多，说明其中包括了绝大部分信息。如果我们只要前三个，

M    u ₁σ ₁  v ₁ ^T +  u ₂σ ₂  v ₂ ^T +  u ₃σ ₃  v ₃ ^T

我们就实现了图像的降噪。

Noisy image	Improved image