二叉树

遍历概念

    　所谓遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。
    　遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

遍历方案

1．遍历方案
    　从二叉树的递归定义可知，一棵非空的二叉树由根结点及左、右子树这三个基本部分组成。因此，在任一给定结点上，可以按某种次序执行三个操作：
    　（1）访问结点本身(N)，
    　（2）遍历该结点的左子树(L)，
    　（3）遍历该结点的右子树(R)。
以上三种操作有六种执行次序：
    　NLR、LNR、LRN、NRL、RNL、RLN。
  注意：
    　前三种次序与后三种次序对称，故只讨论先左后右的前三种次序。

2．三种遍历的命名
    　根据访问结点操作发生位置命名：
　　① NLR：前序遍历(PreorderTraversal亦称(先序遍历))
         ——访问结点的操作发生在遍历其左右子树之前。
　　② LNR：中序遍历(InorderTraversal)
        ——访问结点的操作发生在遍历其左右子树之中(间)。
 　　③ LRN：后序遍历(PostorderTraversal)
        ——访问结点的操作发生在遍历其左右子树之后。
  注意：
    　由于被访问的结点必是某子树的根，所以N(Node)、L(Left subtlee)和R(Right subtree)又可解释为根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。

遍历算法

1．中序遍历的递归算法定义：
    　若二叉树非空，则依次执行如下操作：
         (1)遍历左子树；
         (2)访问根结点；
         (3)遍历右子树。

2．先序遍历的递归算法定义：
   　若二叉树非空，则依次执行如下操作：
         (1) 访问根结点；
         (2) 遍历左子树；
         (3) 遍历右子树。

3．后序遍历得递归算法定义：
   　若二叉树非空，则依次执行如下操作：
         (1)遍历左子树；
         (2)遍历右子树；
         (3)访问根结点。

4．中序遍历的算法实现
    　用二叉链表做为存储结构，中序遍历算法可描述为：
      void InOrder(BinTree T)
        { //算法里①~⑥是为了说明执行过程加入的标号
          ① if(T) { // 如果二叉树非空
          ②    InOrder(T->lchild)；
          ③    printf("％c"，T->data)； // 访问结点
          ④    InOrder(T->rchild);
          ⑤  }
          ⑥ } // InOrder

一、红黑树的介绍

先来看下算法导论对R-B Tree的介绍：
红黑树，一种二叉查找树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。
通过对任何一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其
他路径长出俩倍，因而是接近平衡的。

 

前面说了，红黑树，是一种二叉查找树，既然是二叉查找树，那么它必满足二叉查找树的一般性质。
下面，在具体介绍红黑树之前，咱们先来了解下 二叉查找树的一般性质：
1.在一棵二叉查找树上，执行查找、插入、删除等操作，的时间复杂度为O（lgn）。
    因为，一棵由n个结点，随机构造的二叉查找树的高度为lgn，所以顺理成章，一般操作的执行时间为O（lgn）。
    //至于n个结点的二叉树高度为lgn的证明，可参考算法导论 第12章 二叉查找树 第12.4节。
2.但若是一棵具有n个结点的线性链，则此些操作最坏情况运行时间为O（n）。

 

而红黑树，能保证在最坏情况下，基本的动态几何操作的时间均为O（lgn）。

ok，我们知道，红黑树上每个结点内含五个域，color，key，left，right，p。如果相应的指针域没有，则设为NIL。

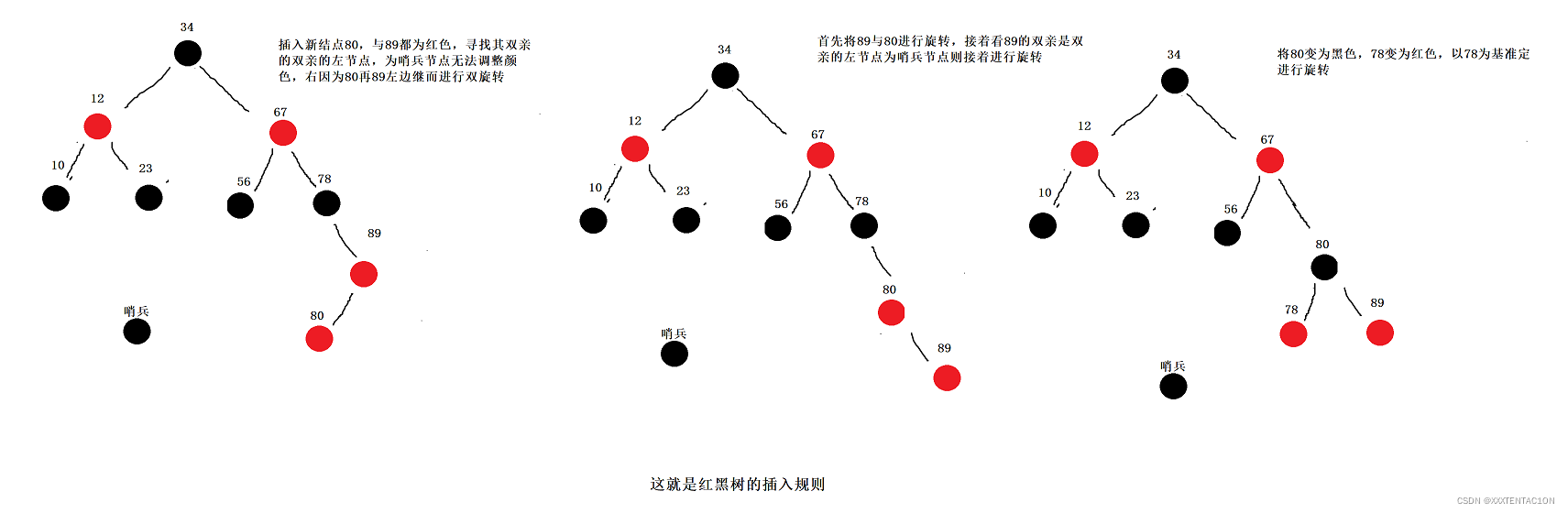
一般的，红黑树，满足以下性质，即只有满足以下全部性质的树，我们才称之为红黑树：

1）每个结点要么是红的，要么是黑的。
2）根结点是黑的。
3）每个叶结点，即空结点（NIL）是黑的。
4）如果一个结点是红的，那么它的俩个儿子都是黑的。
5）对每个结点，从该结点到其子孙结点的所有路径上包含相同数目的黑结点。

 

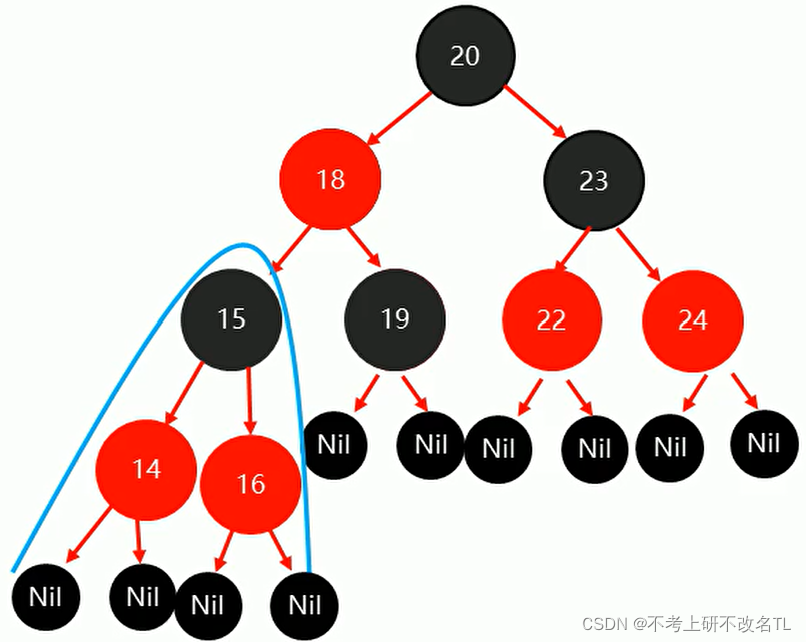
下图所示，即是一颗红黑树：

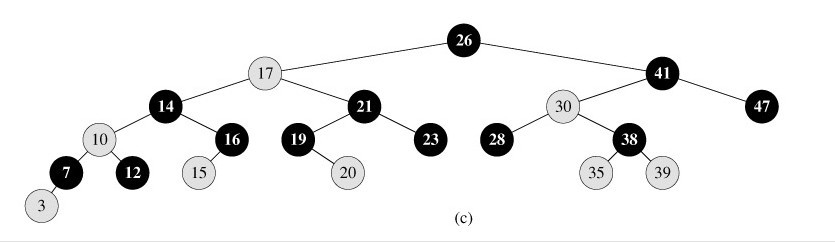
此图忽略了叶子和根部的父结点。

 

二、树的旋转知识

 

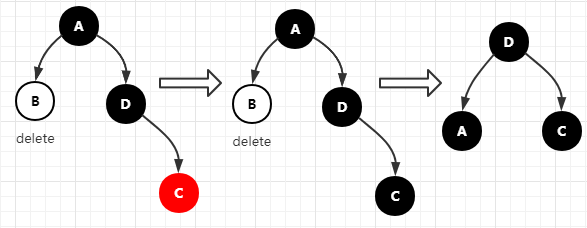
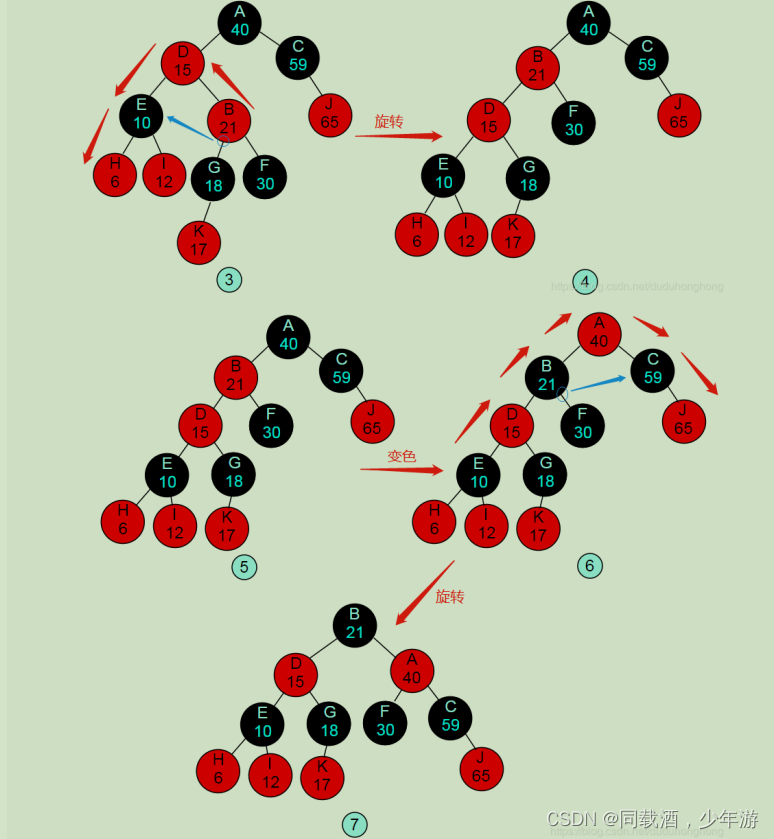
当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性质。

 

为了保持红黑树的性质，我们可以通过对树进行旋转，即修改树种某些结点的颜色及指针结构，以达到对红黑树进行

插入、删除结点等操作时，红黑树依然能保持它特有的性质（如上文所述的，五点性质）。

 

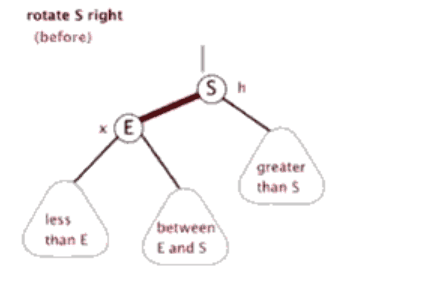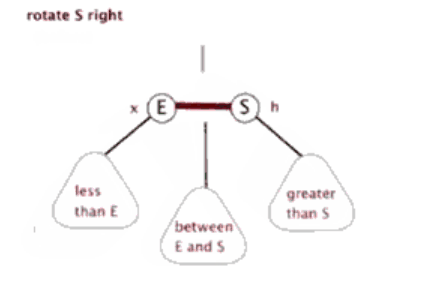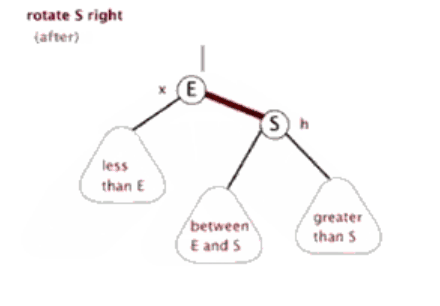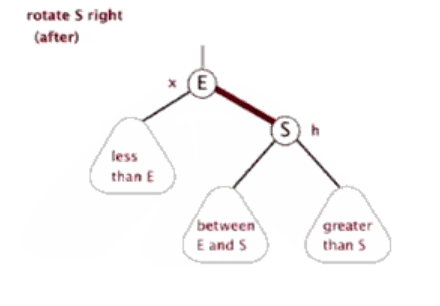
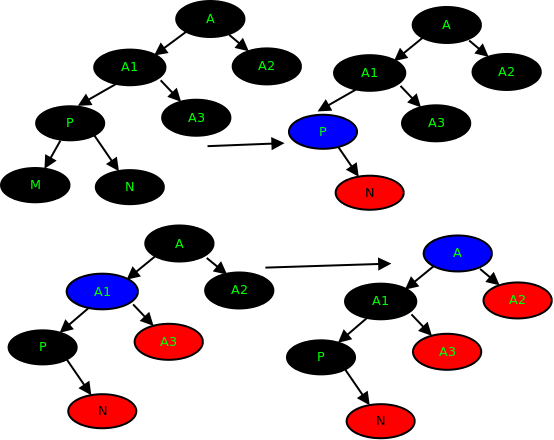
树的旋转，分为左旋和右旋，以下借助图来做形象的解释和介绍：

1.左旋

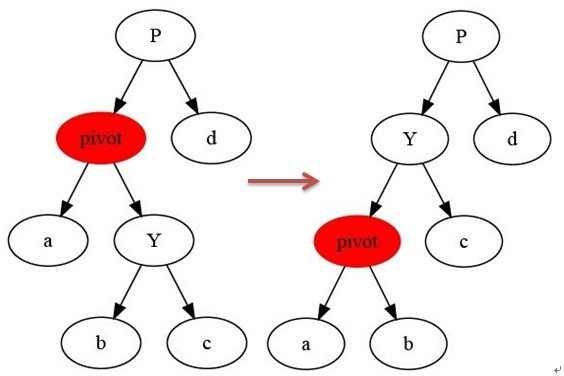
如上图所示：

当在某个结点pivot上，做左旋操作时，我们假设它的右孩子y不是NIL[T]，pivot可以为树内任意右孩子而不是NIL[T]的结点。

左旋以pivot到y之间的链为“支轴”进行，它使y成为该孩子树新的根，而y的左孩子b则成为pivot的右孩子。

更详细请看：http://blog.chinaunix.net/uid-26575352-id-3061918.html

用JAVA代码实现红黑树：http://blog.csdn.net/flyingpig4/article/details/5377839

JAVA二叉树

public class BinaryTree {
TreeNode root;
public TreeNode find(int key){
TreeNode currNode=root;
while(currNode.id!=key){
if(key<currNode.id){
currNode=currNode.leftnode;
}else{
currNode=currNode.rightnode;
}
}
return currNode;
}
public void insert(TreeNode newTd){
TreeNode currNode=root;
TreeNode pNode;
if(currNode==null){
currNode=newTd;
}else{
while(true){
pNode=currNode;
if(newTd.id<currNode.id){
currNode=currNode.leftnode;
if(currNode==null) {
pNode.leftnode=newTd;
return;
}
}else{
currNode=currNode.rightnode;
if(currNode==null) {
pNode.rightnode=newTd;
return;
}
}
}
}

}
public TreeNode findMin(){
TreeNode currNode,last = null;
currNode=root;
while(currNode!=null){
last=currNode;
currNode=currNode.leftnode;
}
return last;
}

/*
* 删除只有一个子节点的树
*/
public void deleteOneNode(TreeNode t){
TreeNode pNode=null;
TreeNode currNode=root;
while(currNode.id!=t.id){
pNode=currNode;
if(t.id<currNode.id)currNode=t.leftnode;
else currNode=t.rightnode;
}
/*
* 
*/
}