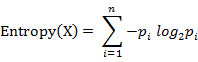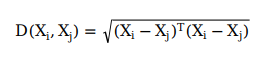1. 免疫算法思想起源

免疫算法是模仿生物免疫机制，结合基因的进化机理，人工构造出的一种新型智能优化算法。

• 它具有一般免疫系统的特征，采用群体搜索策略，通过迭代计算，最终以较大的概率得到问题的最优解。
• 相比较于其他算法，免疫算法利用自身产生多样性和维持机制的特点，保证了种群的多样性，克服了一般寻优过程（特别是多峰值的寻优过程）中不可避免的“早熟”问题，可以求得全局最优解。
• 免疫算法具有自适应性、随机性、并行性、全局收敛性、种群多样性等优点。

2. 算法原理

根据上述的对应关系，模拟生物免疫应答的过程形成了用于优化计算的免疫算法。算法主要包含以下几大模块：

• 抗原识别与初始抗体产生。根据待优化问题的特点设计合适的抗体编码规则，并在此编码规则下利用问题的先验知识产生初始抗体种群。
• 抗体评价。对抗体的质量进行评价，评价准则主要为抗体亲和度和个体浓度，评价得出的优质抗体将进行进化免疫操作，劣质抗体将会被更新。
• 免疫操作。利用免疫选择、克隆、变异、克隆抑制、种群刷新等算子模拟生物免疫应答中的各种免疫操作，形成基于生物免疫系统克隆选择原理的进化规则和方法，实现对各种最优化问题的寻优搜索。

3. 免疫算法算子

3.1 算法算子

免疫算法的算子包括：亲和度评价算子、抗体浓度评价算子、激励度计算算子、免疫选择算子、克隆算子、变异算子、克隆抑制算子和种群刷新算子等。由于算法的编码方式可能为实数编码、离散编码等，不同编码方式下的算法算子也会有所不同。

3.1.1 亲和度评价算子

• 亲和度评价表征算子免疫细胞与抗原的结合强度。
• 亲和度评价算子通常是一个函数$aff(x)：S\in R$ ，
• 其中 $S$ 为问题的可行解区间，$R$ 为实数域。函数的输入为一个抗体个体（可行解），输出即为亲和度评价结果。

3.1.2 抗体浓度评价算子：

抗体浓度评价表征算子抗体种群的多样性好坏。抗体浓度过高意味着种群中非常类似的个体大量存在，不利于全局优化。

• 抗体浓度通常定义为：

  

• 式中： $N$ 为种群规模； $S(a{b}_i,a{b}_j)$ 表示抗体间的相似度，可表示为：

其中 $a{b}_i$ 为种群中的第 $i$ 个抗体，$aff(a{b}_i,a{b}_j)$为抗体 $i$ 与抗体$j$ 的亲和度，${\delta }_s$ 为相似度阈值。

3.1.3 激励度计算算子

• 抗体激励度是对抗体质量的最终评价结果，需要综合考虑抗体亲和度和抗体浓度，通常亲和度大、浓度低的抗体会得到较大的激励度。

• 抗体激励度的计算通常可以利用抗体亲和度和抗体浓度的评价结果进行简单的数学运算得到，如：

  
  式中：$sim(a{b}_i)$为抗体 $a{b}_i$ 的激励度；$a、b$ 为计算参数，可以根据实际情况确定。

3.1.4 免疫选择算子

• 免疫选择算子根据抗体的激励度确定选择哪些抗体进入克隆选择操作
• 在抗体群中激励度高的抗体个体具有更好的质量，更有可能被选中进行克隆选择操作，在搜索空间中更有搜索价值。

3.1.5 克隆算子

克隆算子将免疫选择算子选中的抗体个体进行复制。克隆算子可以描述为：

式中：$clone(a{b}_i)$ 为 $m_i$ 个与 $a{b}_i$ 相同的克隆构成的集合； $m_i$ 为抗体克隆数目，可以事先确定，也可以动态自适应计算。

3.1.6 变异算子

• 变异算子对克隆算子得到的抗体克隆结果进行变异操作，以产生亲和度突变，实现局部搜索。
• 变异算子是免疫算法中产生有潜力的新抗体、实现区域搜索的重要算子，它对算法的性能有很大影响。
• 变异算子也和算法的编码方式相关，实数编码的算法和离散编码的算法采用不同的变异算子。

3.1.7 实数编码变异算子

实数编码算法的变异策略是在变异源个体中加入一个小扰动，使其稍偏离原来的位置，落入源个体邻域中的另一个位置，实现变异源邻域的搜索。实数编码算法变异算子可以描述:

• 式中： $a{b}_{i,j,m}$ 是抗体 $a{b}_i$ 的第 $m$ 个克隆体的第 $j$ 维； $\delta$为定义的邻域的范围，可以事先确定，也可以根据进化过程自适应调整；$rand$ 是产生$(0，1)$ 范围内随机数的函数； $p_m$ 为变异概率。

3.1.8 离散编码变异算子

离散编码算法以二进制编码为主，其变异策略是从变异源抗体串中随机选取几位元，改变位元的取值（取反），使其落在离散空间变异源的邻域。

3.1.9 克隆抑制算子

• 克隆抑制算子用于对经过变异后的克隆体进行再选择，抑制亲和度低的抗体，保留亲和度高的抗体进入新的抗体种群。
• 在克隆抑制的过程中，克隆算子操作的源抗体与克隆体经变异算子作用后得到的临时抗体群共同组成一个集合，克隆抑制操作将保留此集合中亲和度最高的抗体，抑制其他抗体。
• 由于克隆变异算子操作的源抗体是种群中的优质抗体，而克隆抑制算子操作的临时抗体集合中又包含了父代的源抗体，因此在免疫算法的算子操作中隐含了最优个体保留机制。

3.1.10 种群刷新算子

• 种群刷新算子用于对种群中激励度较低的抗体进行刷新，
• 从抗体种群中删除这些抗体并以随机生成的新抗体替代，
• 有利于保持抗体的多样性，实现全局搜索，探索新的可行解空间区域

3.2 亲和度计算方法

3.2.1 基于欧氏实数距离的抗体间亲和度计算方法

• 对于实数编码的算法，抗体间亲和度计算通常可以通过抗体向量之间的欧氏距离来计算：
  
  式中： $a{b}_{i,k}$ 和 $a{b}_{j,k}$ 分别为抗体 $i$ 的第 $k$ 维和抗体 $j$ 的第 $k$ 维， $L$ 为抗体编码总维数。

3.2.2 基于海明距离的抗体-抗体亲和度计算方法

• 对于离散编码的算法，衡量抗体-抗体方法亲和度最直接的方法就是利用抗体串的海明距离：
  
  式中
  
  $a{b}_{i,k}$ 和 $a{b}_{j,k}$ 分别为抗体 $i$ 的第 $k$ 位和抗体 $j$ 的第 $k$ 位， $L$ 为抗体编码长度。

4. 免疫算法种类和流程

4.1 免疫算法种类

4.1.1 克隆选择算法

Castro提出了基于免疫系统的克隆选择理论的克隆选择算法，该算法是模拟免疫系统学习过程的进化算法。

• 免疫应答产生抗体是免疫系统的学习过程，抗原被一些与之匹配的B细胞识别，这些B细胞分裂，产生的子B细胞在母细胞的基础上发生变化，以寻求与抗原匹配更好的B细胞，
• 与抗原匹配更好的子B细胞再分裂……如此循环往复,最找到与抗原完全匹配的B细胞，B细胞变成浆细胞产生抗体，这一过程就是克隆选择过程，

4.1.2免疫遗传算法

Chun 等人提出了一种免疫算法，实质上是改进的遗传算法 。

• 根据体细胞和免疫网理论改进了遗传算法的选择操作，从而保持了群体的多样性，提高算法的全局寻优能力。
• 通过在算法中加入免疫记忆功能，提高了算法的收敛速度。
• 免疫遗传算法把抗原看作目标函数，将抗体看作问题的可行解，抗体与抗原的亲和度看作可行解的适应度。
• 免疫遗传算法引入了抗体浓度的概念，并用信息熵来描述，表示群体中相似可行解的多少。
• 免疫遗传算法根据抗体与抗原的亲和度和抗体的浓度进行选择操作，亲和度高且浓度小的抗体选择率大，这样就抑制了群体中浓度高的抗体，保持了群体的多样性。

4.1.3 反向选择算法

Forrest基于反向选择原理提出了反向选择算法，用于进行异常检测。算法主要包括两个步骤：

• 首先，产生一个检测器集合，其中每一个检测器与被保护的数据不匹配；
• 其次，不断地将集合中的每一个检测器与被保护数据相比较，如果检测器与被保护数据相匹配，则判定数据发生了变化。

4.1.4 疫苗免疫算法

焦李成等人基于免疫系统的理论提出了基于疫苗的免疫算法，该算法是在遗传算法中加入免疫算子，以提高算法的收敛速度并防止群体退化。
免疫算子包括疫苗接种和免疫选择两个部分，前者为了提高亲和度，后者为了防止种群退化。理论分析表明这种免疫算法是收敛的。

疫苗免疫算法的基本步骤是：

• 随机产生 $NP$ 个个体构成初始父代群体；
• 根据先验知识抽取疫苗；
• 计算当前父代NP种群所有个体的亲和度，并进行停止条件的判断；
• 对当前的父代群体进行变异操作，生成子代群体；
• 对子代群体进行疫苗接种操作，得到新种群；
• 对新群体进行免疫选择操作，得到新一代父本，并进入免疫循环。

4.2 免疫算法的算法流程

免疫算法运算流程如图4.1所示：

• (1) 首先进行抗原识别，即理解待优化的问题，对问题进行可行性分析，提取先验知识，构造出合适的亲和度函数，并制定各种约束条件。
• (2) 然后产生初始抗体群，通过编码把问题的可行解表示成解空间中的抗体，在解的空间内随机产生一个初始种群。
• (3) 对种群中的每一个可行解进行亲和度评价。
• (4) 判断是否满足算法终止条件：如果满足条件，则终止算法寻优过程，输出计算结果；否则，继续寻优运算。
• (5) 计算抗体浓度和激励度。
• (6) 进行免疫处理，包括免疫选择、克隆、变异和克隆抑制。

• 种群刷新，以随机生成的新抗体替代种群中激励度较低的抗体，形成新一代抗体，转步骤 (3)。

5. 关键参数说明与算法特点

5.1 关键参数说明

5.2 算法特点

• 全局搜索能力。模仿免疫应答过程提出的免疫算法是一种具有全局搜索能力的优化算法
• 多样性保持机制。对抗体进行浓度计算，并将浓度计算的结果作为评价抗体个体优劣的一个重要标准；它使浓度高的抗体被抑制，保证抗体种群具有很好的多样性，这也是保证算法全局收敛性能的一个重要方面。
• 鲁棒性强。基于生物免疫机理的免疫算法不针对特定问题，而且不强调算法参数设置和初始解的质量，利用其启发式的智能搜索机制，即使起步于劣质解种群，最终也可以搜索到问题的全局最优解，对问题和初始解的依赖性不强，具有很强的适应性和鲁棒性。
• 并行分布式搜索机制。免疫算法不需要集中控制，可以实现并行处理。尤其适合于多模态的优化问题。

参考

《智能优化算法及其matlab实例 (第二版)》