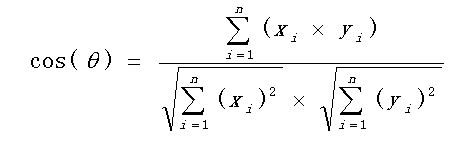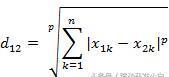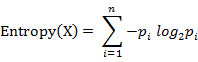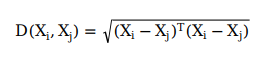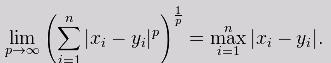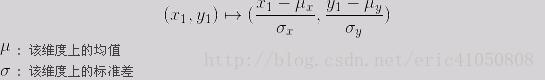免疫算法（Immune Algorithm)详解

关于免疫算法（IA），其功能与遗传算法、模拟退火等算法实现的功能是相同的，都是用来求最优解。例如求函数最值、旅行商问题等。从本质上说，免疫算法更像是遗传算法的一种延申。IA虽然其中借鉴了生物学（免疫学）的概念，但学习时需要注意，IA毕竟是一种算法，把算法中所有概念都与免疫学概念联系起来是容易难以理解算法的，甚至容易混淆。所以IA只是借鉴免疫学概念并受免疫过程的启发，最终其实还是需要回归到算法当中。

即便如此，兔兔在后面还是需要将算法与一些生物学概念联系，但是会辨别其中本质区别。而且学习时需要与遗传算法相结合，毕竟免疫算法从某种角度来说是遗传算法的一种延申。

（1）相关免疫学知识与IA算法

根据高中的生物学知识，我们知道，抗原（细菌、病毒、疫苗等）进入生物体后，首先会被非特异性免疫消灭，但有时这种免疫防线会被突破。所以还有特异性免疫，即B细胞受抗原刺激后分化成浆细胞和记忆细胞，浆细胞分泌抗体抑制消灭抗原。记忆细胞在下次接受抗原时可以直接分化成浆细胞并分泌抗体，抑制抗原。

上面的概念虽然很多，但实际在算法中很多相关概念和过程是可以合并或忽略的。

在遗传算法中，我们把种群中的个体（即染色体）当作解，先初始种群（初始解），在进行交叉、突变、选择；这里的抗原、抗体在一开始时就代表初始解，抗原抗体在一开始是混在一起的，只不过我们把较优的一部分解叫“抗原”，不优的部分叫做”抗体“。之后的每次迭代过程我们叫做“打疫苗”。

在免疫学中，我们知道，当生物体接种疫苗后，相应的B细胞分化成浆细胞与记忆细胞，再次注射疫苗时记忆细胞在抗原刺激性又会分化成浆细胞，从而分泌更多的抗体。而且，免疫学中，抗原抗体，抗原与记忆细胞的识别是特异性结合的。在我们IA算法中，抗原抗体是几乎没有特异性结合这种过程的（有的文章中会把序列识别等当作特异性识别，其实是不准确的，不必在意）。而且，IA算法中几乎不区分浆细胞、记忆细胞、抗原这三者的概念的，或者说，这三者表示算法中同一个东西。算法中表示接种疫苗的过程是：把之前的抗原克隆复制（即把这些解复制多次），对这些克隆进行突变，选取较优的部分作新抗原（即新的较优解），再把这些抗原与新的疫苗抗体（即新的一些随机解）混合在一起（这个过程可以看作是接种疫苗），在从这些混合解中选取较优的部分作为新的抗原，这个新的抗原在进入下一次接种疫苗的过程中。在从混合解中选的过程中，我们也淘汰了一些不优的解，可以对应是抗体免疫抑制抗原（其中其实也包括了抗原复制扩增对抗体的一种抑制），但本质就是从中选较优的解，与是否是免疫抑制关系不是很大（但很多文章会是这样讲的）。

如果从现在来看的话，免疫算法与遗传算法区别并不是很大，主要就是除了之前的突变、交叉操作，多了一个接种疫苗的操作——即每次选一部分较优解（抗原、记忆细胞、浆细胞）复制选优后与随机解混合，从中选取较优解（抗原），再进行重复操作。

但是在免疫算法选择的步骤中，对遗传算法中由“适应度”进行选择的方法做了很大改进，引出了“亲和度”（affinity)、"抗体浓度"（density)、"激励度"（simulation)这三个在选择操作中的重要概念。其中的激励度是由亲和度与抗体浓度进行计算的。亲和度与抗体浓度是由这些解来计算的。

“亲和度”（affinty)本质上就是遗传算法中的“适应度”（fitness),所以亲和度本质上代表解与最优情况的接近程度。例如，当我们求函数f(x)的最大值时，亲和度就可以用f(x)来表示，f(x)越大，亲和度也就越大。

“抗体浓度”（density)本质上是一个解与集合中其它所有的解当中距离比较近(或者说比较相似）的解的个数，再除以集合中解的总数总数就是这个解的浓度，称作抗体浓度（准确来说就是浓度，因为集合是抗原抗体的混合）。那么怎么判断一个解与其它所有解距离较近的个数呢？

所以我们需要一种方法来度量距离，并且当距离小于某一个阈值（delta)时判断这个解就是其中一个离它比较近的解，否则不是。所以我们需要找到解直接的一种距离度量方法。（注；很多文章会说两个解之间的相似程度或距离叫做亲和度，并把计算距离或相似程度这个过程叫做亲和力计算，这样在算法中不太准确，而且会和前面那个亲和度概念弄混）。

距离度量方法

（1）实数编码的解。

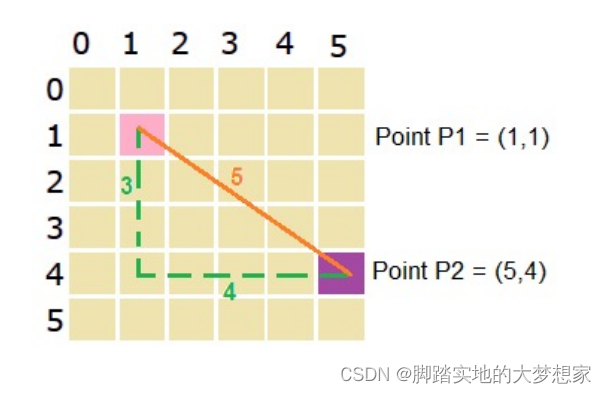
对于实数编码的解，通常可以用欧氏距离来表示，如果是一维的数，就是两个数相减绝对值；如果是二维平面的点，就是平面两点距离公式：

$distance(a,b)=\sqrt{(a_{x}-b_{x})^{2}+(a_{y}-b_{y})^{2}}$

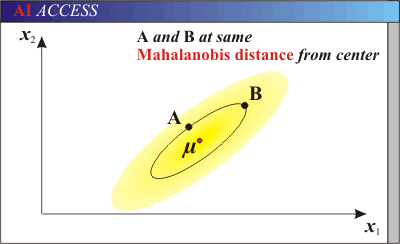
多维的点以此类推。除了欧式距离，还有马式距离、闵式距离等，在多元统计、泛函分析等学科都有涉及，IA算法大多采用欧式距离。

（2）离散编码的解。

一般情况下，我们遇到的离散的解就是二进制的长串（兔兔在遗传算法中曾使用过，详解《遗传算法（GA）详解》一文）。如[0,1,1,1,0,0,1,0]。对于这种情况通常采用海明距离。

$distance(a,b)=\sum_{i=1}^{k}x_{k}$

其中 $x_{k}=\begin{Bmatrix}0 &a_{k}=b_{k}\\1&a_{k}\neq b_{k} \end{}$ ,ak,bk分布表示各自数组中位置k的元素（1或0）。这样两个链对应位置不一样的位置越多，距离就越远，很符合逻辑。

那么，现在我们找到了距离度量方法，当距离小于阈值delta时就认为两个解接近，然后累计该解与所有解距离近的个数，最后除以解的总个数就是该解的浓度了。

“激励度”（simulation)就是最终选择的评判标准了。激励度公式如下：

$simulation=alpha\times affinity-beta\times density$

其中alpha通常是1，beta=2，实际可以根据需要进行调整。一个解的激励度越大，那么就越先优选。对应就是遗传算法在“适应度”——适应度越大，被选概率越大。只不过这里有了density一项的影响，只要simulation大，我们就一定选这个解，而不是以大的概率取选它。我们根据simulation选解的操作是：把解按照simulation的大小从大往小排，取其中simulation较大的前一半作为抗原（选较优解），后面一半全都不要；之后操作：克隆（把抗原复制多个），随机突变，再把这些计算simulation，按顺序排，取simulation较大的部分，与抗体疫苗混合（接种疫苗），把这个混合集合再计算simulation ,排序选较大的部分，就是新的抗体的，之后循环操作。

对simulation的理解

我们发现，如果让式子中beta一项为0，那么就是适应度（fitness)，即每次选择适应度最大的解。而减去了beta*density,就说明density值越大，其simulation就越小，就越可能不被选中。而density代表了这个解与所有解中比较相近的解的个数。所以浓度越低，激励度会越好，越容易被选中。

变异操作

与遗传算法相同，免疫算法在每次对抗体克隆后会对所有克隆进行变异。对于二进制的数组，变异方法与遗传算法中变异操作一致。而对于实数编码，变异操作可以表示为：

$T(a)=\begin{Bmatrix} a+(rand-0.5)& if:\delta &rand<pm\\a&if:&other\end{}$

rand是0~1随机数，如果小于pm(即以概率pm选择是否突变），就进行突变， $\delta$ 表示定义域区间长度。大于pm就不突变。

关于交叉操作，在IA中也是可以有的，但是有了变异操作，又有接种疫苗的操作，导致每次都有很大的随机性，所以多数情况是可以不用交叉。交叉操作与遗传算法中交叉操作一致。

（2）算法总结

在网上或其它文章中我们都可以看到关于免疫算法的流程图，而且有很多种，里面大多都是免疫学的概念，但其实回到算法当中，无外乎都是同种东西。所以关键还是算法流程，免疫学概念可以用来进行比喻帮助记忆。

（1）先初始n个解，n为种群个数。

（2）计算这些种群的亲和度、浓度，并计算出激励度。

（3）根据激励度对种群由大到小排列，取前n/2个做抗原，后面的不要。

（4）对抗原进行克隆，克隆m份，对mn/2个克隆进行变异。

（5）变异后计算亲和度、浓度，并计算激励度。根据激励度大小从大到小排列，取前n/2个做抗体。

（6）随机产生n/2个种群（即疫苗、抗体），与前面得到的抗体混合。

（7）混合后计算亲和度、浓度，并计算激励度，根据激励度从大到小排列，取前n/2做抗体。

（8）得到的抗体再回到（4），重复循环。

（9）在循环结束后，根据affinity排序，选取affinity最大的那个解作为最优解。

以上就是免疫算法的基本流程。

（3）算法实现

我们以求函数f(x)=sin(3x) （ $x\epsilon (0,4)$ )求最大值为例。我们编码解的二进制数组长度binarylength为8，初始种群数popsize=40,突变概率pm为0.7，阈值delta=3,克隆数clone_num为10，alpha=1,beta=1,循环次数circle=30。

import numpy as np
class IA:def __init__(self,circle=30,pm=0.7,alpha=1,beta=1,delta=3,popsize=40,binarylength=8,area=4,clone_num=10):self.circle=circle #循环次数self.pm=pm #突变概率self.clone_num=clone_num #克隆数self.alpha=alphaself.beta=betaself.delta=delta #阈值self.binarylength=binarylength #二进制数组长度self.pop=np.random.randint(0,2,size=(popsize,binarylength)) #随机初始popsize个种群self.area=area #即domain of definition,定义域，这里简写成areadef bin_to_dec(self,pop):'''把种群中所有二进制数组转换成0~4之间的十进制数'''n=pop.shape[0]p=pop.shape[1]s=np.zeros(shape=(n,1))for i in range(self.binarylength):s+=pop[:,i].reshape(n,1)*2**(p-i-1)return self.area*s/2**pdef mutation(self,pop):'''进行变异操作'''n,p=pop.shapefor i in range(n):if np.random.rand()<self.pm:point=np.random.randint(0,p) #随机选位点突变if pop[i,point]==1:pop[i,point]=0else:pop[i,point]=1return popdef simulation(self,affinity,density):计算激励度return self.alpha*affinity-self.beta*densitydef density(self,pop):'''计算浓度'''n,p=pop.shapeden = [] #用来储存每一个解对应浓度j=0for i in range(n):judge=0 #保存所有与i点距离达到阈值的个数for j in range(n):s=0 #保存二进制数组中对应位置数字不同的个数for k in range(p):if pop[i,k]==pop[j,k]:s+=1if s<self.delta: #判断是否达到阈值judge+=1den.append(judge)return np.array(den)/ndef affinity(self,pop):'''亲和度计算'''p=self.bin_to_dec(pop=pop)p=p.reshape(1,-1)[0]p=p.astype('float') #转换数据类型，否则np.sin(3*p)会报错return np.sin(3*p)def main(self):'''主程序'''initpop=self.pop #初始化种群density=self.density(pop=initpop)affinity=self.affinity(pop=initpop)simulation=self.simulation(affinity,density)index=np.argsort(-simulation) #根据激励度从大到小排序pop=initpop[index]n,p=pop.shapebest_pop = pop[0:int(n / 2), :] #选出前n/2作为抗体#开始进行circle次循环操作for c in range(self.circle):print('the {} circle'.format(c)) #显示循环次数clone=best_popfor i in range(self.clone_num-1): #开始进行克隆clone=np.r_[clone,best_pop]clone=self.mutation(pop=clone) #对克隆变异clone_density=self.density(pop=clone)clone_affinty=self.affinity(pop=clone)clone_simulation=self.simulation(affinity=clone_affinty,density=clone_density) #计算激励度index=np.argsort(-clone_simulation) #根据激励度排序newpop=clone[index][0:int(n/2),:] #选出抗体antigen=np.random.randint(0,2,size=(int(n/2),p)) #随机初始一些解做抗原combin_pop=np.r_[newpop,antigen] #把抗原抗体结合density=self.density(pop=combin_pop) #计算结合后的浓度affinity=self.affinity(pop=combin_pop)simulation=self.simulation(affinity,density)index=np.argsort(-simulation)combin_pop=combin_pop[index][0:int(n/2),:]best_pop=combin_pop #选出抗体，回到初始步骤进行循环return best_pop
if __name__=='__main__':ia=IA()best_pop=ia.main()result=ia.bin_to_dec(pop=best_pop) #把结果转换成十进制数x=np.arange(0,4,0.1)y=np.sin(3*x)plt.plot(x,y) #画函数图像plt.scatter(result,np.sin(3*result)，color='red') #画解的散点图plt.show()

程序运行结果如下：

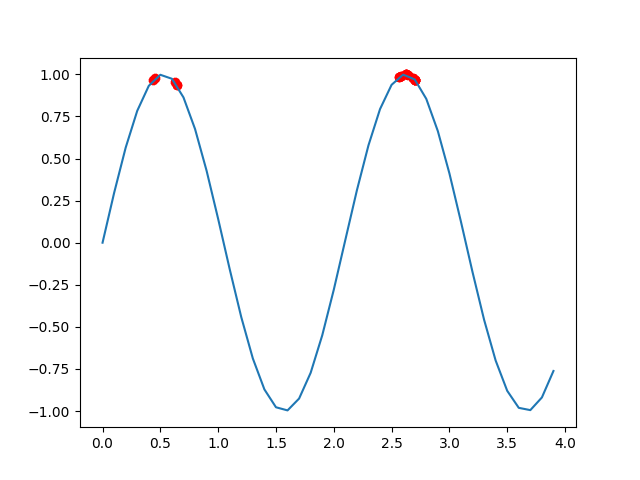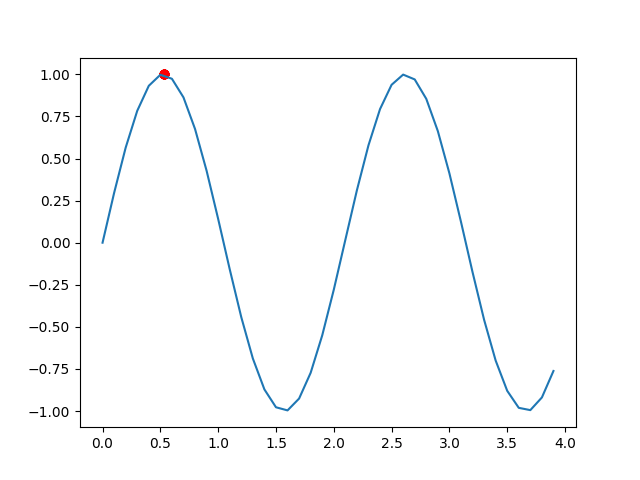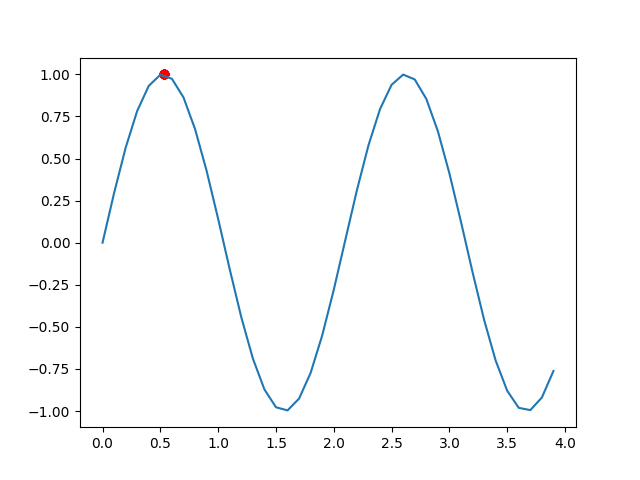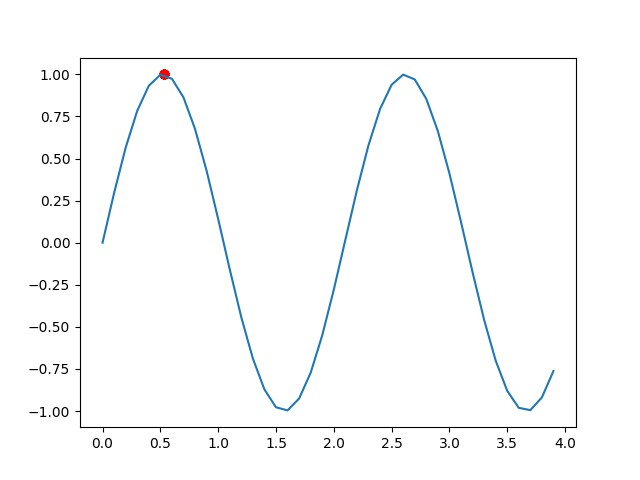
我们可以看到，结果很快就在最大值附近了，说明效果很好。

值得注意的是，随着循环的进行，结果离最优越来越近，我们这时应该逐渐减小变异概率pm，当达到最优时，我们是不希望他变异很大，这样不容易稳定在最优解，所有可以设置pm[i]=pm0/c[i]，即第i次循环的变异概率为初始的突变概率pm除以循环次数。

对于求二元函数最值，我们一般按照实数编码的方式，很少用二进制编码。过程也是相同的，只是相似的（距离）度量一般采用欧式距离，阈值通常也比较小。

（4）总结

免疫算法从本质上说是遗传算法的一种延申，而遗传算法更像是对蒙特卡罗模拟的一种改进。在蒙特拉罗模拟中，我们只是随机初始解并选择最优；在遗传算法中，由于交叉于变异的出现，使得解有很大的随机性并可以找到最优，并在选择中以大的概率保留下来；在免疫算法中，由于接种疫苗过程的出现，以及基于亲和度、浓度计算出的激励度的选择方法，使得随机性比遗传算法更大，同时也能够很好地达到全局最优。