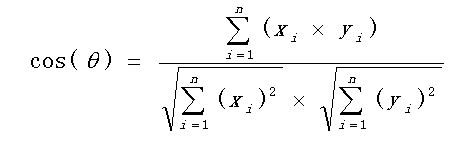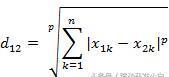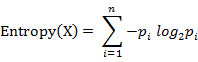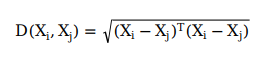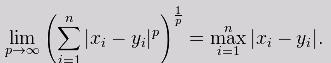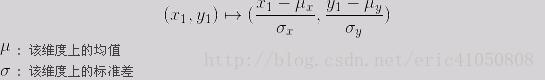免疫算法是将免疫概念及其理论应用于遗传算法，在保留原算法优良特性的前提下，利用抗体浓度评价算子和激励度计算算子来保持群体的多样性，克服了一般寻优过程中（特别是多峰值）不可避免的“早熟”问题。

1 算法概念

免疫算法是受生物免疫系统的启发而推出的一种新型的智能搜索算法。 

2 主要特点

全局搜索能力

多样性保持机制

鲁棒性强

并行分布式搜索机制

3 算法流程

3.1 产生初始抗体种群

基于概率随机生成。

3.2 计算亲和度

依据函数值或函数值的简单处理（倒数、相反数），亲和度表示为aff。

3.3 计算抗体浓度和激励度

抗体浓度表征抗体种群的多样性好坏，浓度高代表种群相似大量存在，抗体浓度表示为den。

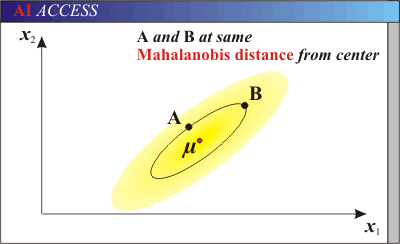
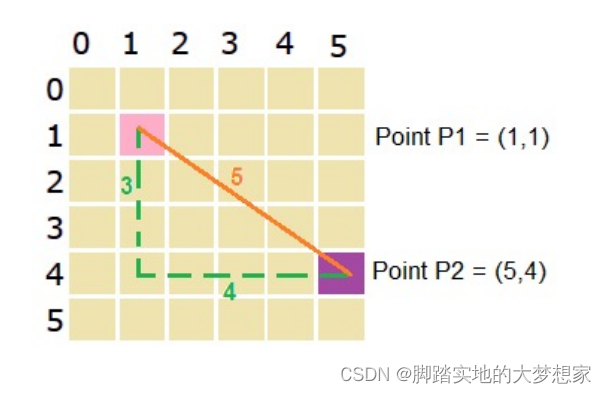
有3中方法计算浓度：基于欧式距离、基于海明距离、基于信息熵。

激励度是对抗体质量的最终评价结果，通常通过对抗体亲和度aff和抗体浓度den进行简单数学运算得到，激励度sim=a*aff-b*den，其中a，b为计算参数。

3.4 免疫处理

免疫选择，选择亲和度靠前的部分进行免疫处理，一般取前NP/2，使其活化。

克隆，对活化的抗体进行克隆复制。

变异，对克隆副本进行变异操作，保留被克隆抗体，主要针对亲和度。

克隆抑制，对变异结果进行筛选，保留亲和度高的变异结果。

3.5 种群刷新

随机生成部分新的抗体种群，与免疫处理的抗体合并，形成新一代抗体。

4 关键参数

4.1 抗体种群大小NP

取10-100合适，一般不超过200。

4.2 免疫选择比例

一般取NP规模的10%-50%。

4.3 抗体克隆扩增的倍数NC

倍数越大，局部搜索能力越好，但计算量增加，一般取5-10倍。

4.4 最大进化代数G

一般取100-500。

5 仿真实例

5.1 问题描述

TSP-旅行商问题，假如一个商人需要拜访31个省会城市，每个城市只能拜访1次，求拜访的最小路径。

5.2 求解代码

5.2.1 创建初始免疫种群

%%%%%初始化参数
C = [1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;3238 1229;4196 1044;4312 790 ;4386 570 ;3007 1970;2562 1756;2788 1491;2381 1676;1332 695 ;3715 1678;3918 2179;4061 2370;3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;2370 2975];
NP=200;
N=size(C,1);
G=1000;
%%%%%初始种群
f=zeros(N,NP);
for i=1:NPf(:,i)=randperm(N);
end

5.2.2 亲和度计算

len=zeros(1,NP);
%%%%%任意城市间距离
D=zeros(N);
for i=1:Nfor j=1:ND(i,j)=((C(i,1)-C(j,1))^2 + (C(i,2)-C(j,2))^2)^0.5;end
end
%%%%%计算路径长度--亲和度
for i=1:NPlen(i)=func3(D,f(:,i),N);
end
[sortlen ,index]=sort(len);
sortf=f(:,index);
NC=10;
%%%%%路径长度函数
function result = func3(D,f,N)len=D(f(1),f(N));for j=2:Nlen=D(f(j),f(j-1))+len;endresult=len;
end

5.2.3 免疫操作

gen=1;
%%%%%免疫循环
while gen<=G%%%%%选择激励度前NP/2个体进入免疫操作for i=1:NP/2a=sortf(:,i);ca=repmat(a,1,NC);for j=1:NCp1=floor(1+N*rand);p2=floor(1+N*rand);while p1==p2p1=floor(1+N*rand);p2=floor(1+N*rand);endtmp=ca(p1,j);ca(p1,j)=ca(p2,j);ca(p2,j)=tmp;endca(:,1)=a;%%%%%克隆抑制for j=1:NCcalen(j)=func3(D,ca(:,j),N);end[sortcalen,index]=sort(calen);sortca=ca(:,index);af(:,i)=sortca(:,1);alen(i)=sortcalen(1);end

5.2.4 种群刷新

 %%%%%免疫种群与新生种群合并--种群刷新for i=1:NP/2bf(:,i)=randperm(N);blen(i)=func3(D,bf(:,i),N);endf=[af bf];len=[alen blen];[sortlen, index]=sort(len);sortf=f(:,index);gen=gen+1;trace(gen)=sortlen(1);
end

5.2.5 结果输出

%%%%%输出优化结果
figure;
bestf=sortf(:,1);
bestlen=trace(end);
for i=1:N-1plot([C(bestf(i),1),C(bestf(i+1),1)],[C(bestf(i),2),C(bestf(i+1),2)],'o-');hold on;
end
plot([C(bestf(N),1),C(bestf(1),1)],[C(bestf(N),2),C(bestf(1),2)],'ro-');
title(['最短距离：',num2str(bestlen)]);
figure;
plot(trace);
xlabel('迭代次数');
ylabel('目标函数值');
title('亲和度进化曲线');

5.3 问题结果

图3 亲和度进化曲线 

图4 最短路径行程