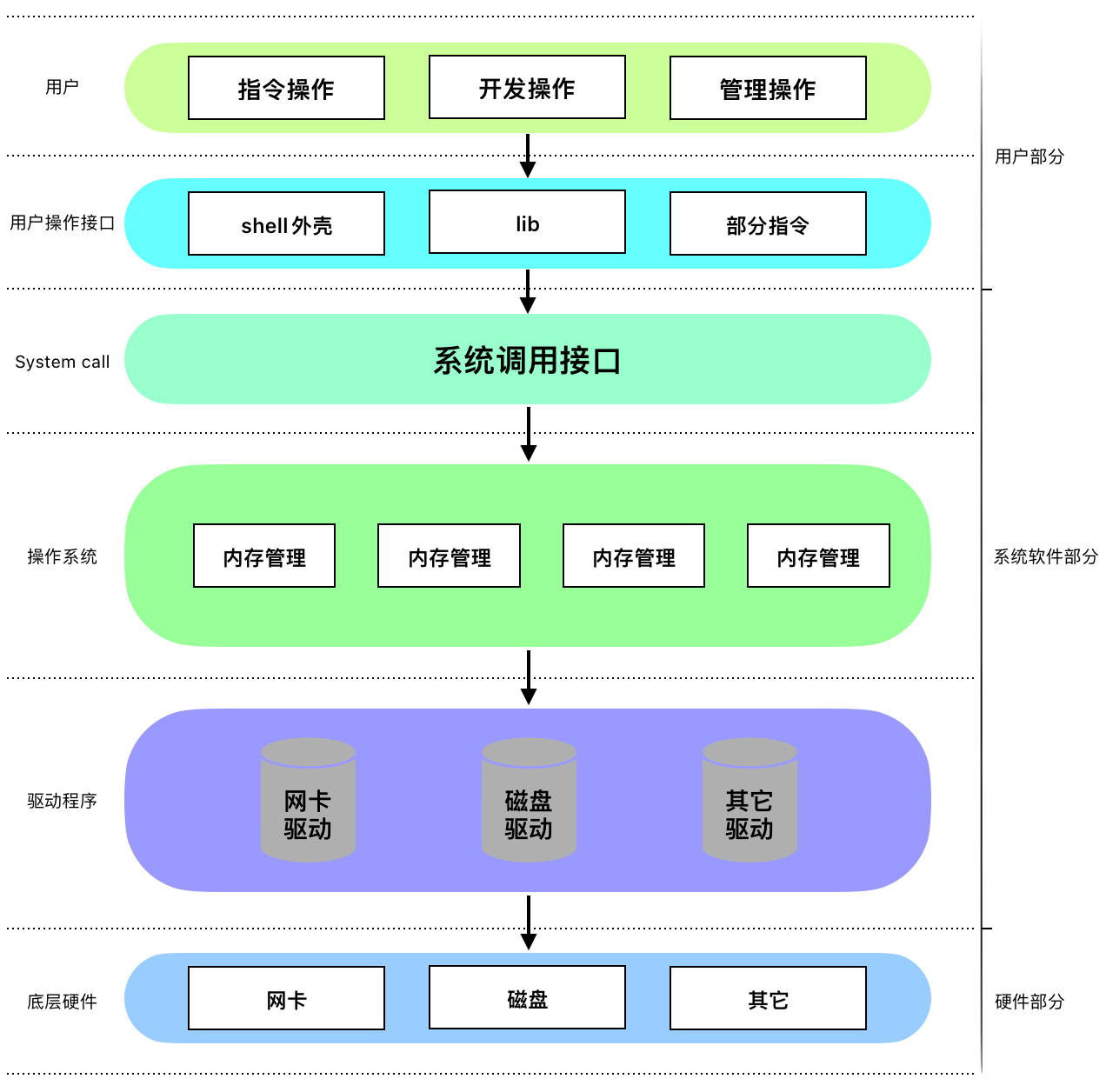
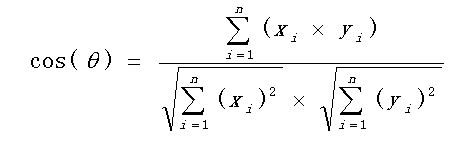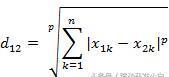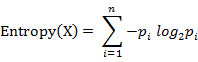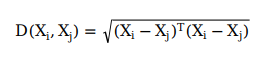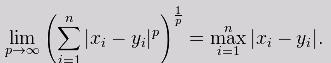免疫算法是受生物免疫系统的启发而推出的一种新型的智能搜索算法,是一种确定性和随机性选择相结合并具有"勘探"与"开采"能力的启发式随机搜索算法。
算法主要的步骤:
(1)抗原识别与初始抗体产生。
(2)抗体评价
(3)免疫操作
免疫算法的特点:
(1)全局搜索能力
(2)多样性保持机制
(3)鲁棒性强
(4)并行分布式搜索机制
免疫算法流程图:
(1)抗原识别,即理解待优化的问题,对问题进行可行性分析,提取先验知识,构造出合适的亲和度函数,并制定各种约束条件。
(2)初始抗体群,通过编码把问题的可行解表示成解空间中的抗体,在解的空间内随机产生一个初始种群。
(3)对种群中的每一个可行解进行亲和度评价。
(4)判断是否满足算法终止条件;如果满足条件则终止算法寻优过程,输出计算结果;否则继续寻优运算。
(5)计算抗体浓度和激励度。
(6)进行免疫处理,包括免疫选择、克隆、变异和克隆抑制。
免疫选择:根据种群中抗体的亲和度和浓度计算结果选择优质抗体,使其活化;
克隆:对活化的抗体进行克隆复制,得到若干副本;
变异:对克隆得到的副本进行变异操作,使其发生亲和度突变;
克隆抑制:对变异结果进行再选择,抑制亲和度低的抗体,保留亲和度高的变异结果。
(7)种群刷新,以随机生成的新抗体替代种群中激励度较低的抗体,形成新一代抗体,转步骤(3)。
免疫算法求解TSP问题:
%%%一个旅行商人要拜访全国31个省会城市,需要选择最短的路径%%%%
%种群数目NP=200
%免疫个体维数N=31
%迭代次数G=1000
%克隆个体个数为Ncl=10
%任意两个城市的距离矩阵D%%%免疫算法解决TSP问题%%%%%%%
%%%初始化%%%%%%%
clear all; %清除所有变量
close all; %清图
clc ; %清屏
%%全国31个省会城市的坐标
C=[
1304 2312;
3639 1315;
4177 2244;
3712 1399;
3488 1535;
3326 1556;
3238 1229;
4196 1004;
4312 790;
4386 570;
3007 1970;
2562 1756;
2788 1491;
2381 1676;
1332 695;
3715 1678;
3918 2179;
4061 2370;
3780 2212;
3676 2578;
4029 2838;
4263 2931;
3429 1908;
3507 2367;
3394 2643;
3439 3201;
2935 3240;
3140 3550;
2545 2357;
2778 2826;
2370 2975
];%31个省会坐标N=size(C,1); %TSP问题的规模,即城市数目
D=zeros(N); %任意两个城市距离间隔矩阵,初始化都为0%任意两个城市距离间隔矩阵%for i=1:Nfor j=1:ND(i,j)=((C(i,1)-C(j,1))^2+(C(i,2)-C(j,2))^2)^0.5;endend NP=200; %免疫个体数目G=1000; %最大免疫代数f=zeros(N,NP); %用于存储种群for i=1:NPf(:,i)=randperm(N); %随机生成初始种群endlen=zeros(NP,1); %存储路径长度for i=1:NPlen(i)=func3(D,f(:,i),N); %随机生成初始种群end[Sortlen,Index]=sort(len);Sortf=f(:,Index); %种群个体排序gen=0; %免疫代数Nc1=10; %克隆个数%%%%%%%%%%%%%%%%%%%%%%免疫循环%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%while gen<G%%%%%%%%%%%%%%%%%选激励度前NP/2个个体进行免疫操作%%%%%%%%%%%for i=1:NP/2a=Sortf(:,i);Ca=repmat(a,1,Nc1);for j=1:Nc1p1=floor(1+N*rand());p2=floor(1+N*rand());while p1==p2p1=floor(1+N*rand());p2=floor(1+N*rand());end%%元素的交换temp=Ca(p1,j);Ca(p1,j)=Ca(p2,j);Ca(p2,j)=temp;endCa(:,1)=Sortf(:,i); %保留克隆源个体%%%%%%%%%%%%%%%%克隆抑制,保留亲和度最高的个体%%%%%%%%%%%%%%%%for j=1:Nc1Calen(j)=func3(D,Ca(:,j),N);end[SortCalen,Index]=sort(Calen);SortCa=Ca(:,Index);af(:,i)=SortCa(:,1);alen(i)=SortCalen(1);end%%%%%%%%%%%%%%%%%种群刷新%%%%%%%%%%%for i=1:NP/2bf(:,i)=randperm(N); %随机生成初始种群blen(i)=func3(D,bf(:,i),N); %计算路径长度end%%%%%%%%%%%%%%%%%免疫种群与新种群合并%%%%%%%%%%%f=[af,bf];len=[alen,blen];[Sortlen,Index]=sort(len);Sortf=f(:,Index);gen=gen+1;trace(gen)=Sortlen(1);end%%%%%%%%%%%%%%%%%%%%%%输出优化结果%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%Bestf=Sortf(:,1); %最优变量Bestlen=trace(end); %最优值%%%%%图1figure for i=1:N-1plot([C(Bestf(i),1),C(Bestf(i+1),1)],...[C(Bestf(i),2),C(Bestf(i+1),2)],'bo-');hold on;endplot([C(Bestf(N),1),C(Bestf(1),1)],...[C(Bestf(N),2),C(Bestf(1),2)],'ro-');title(['优化最短距离:',num2str(trace(end))]);%%%%图2figure plot(trace)xlabel('迭代次数')ylabel('目标函数值')title('亲和度进化曲线')function len=func3(D,f,N)len=D(f(N),f(1));for i=1:(N-1)len=len+D(f(i),f(i+1));endend



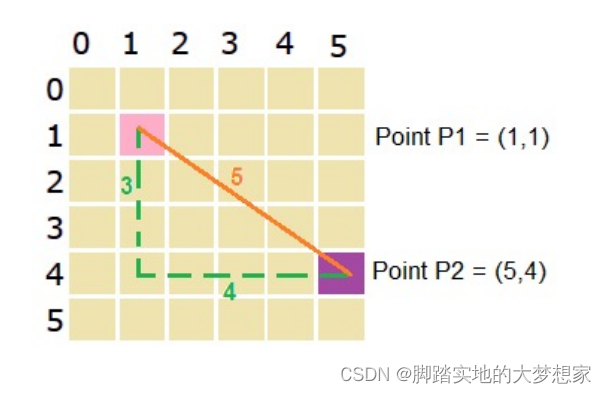
![闵可夫斯基距离—大白话篇幅[有错误的话请指教]](https://img-blog.csdnimg.cn/20190624195707120.png)