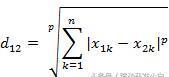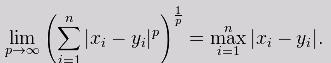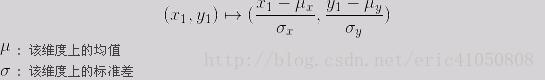题目

定义一个高维空间样本点集类HDPoints，须包含以下数据属性与方法属性：

(a)数据属性self.points：类型为列表，由多个子列表构成，每个子列表表示高维空间中的一个数据点，且数据维度可以任意，并通过初始化构造函数获得。

(b)方法属性centerpoint(self)：计算点集的中心点。

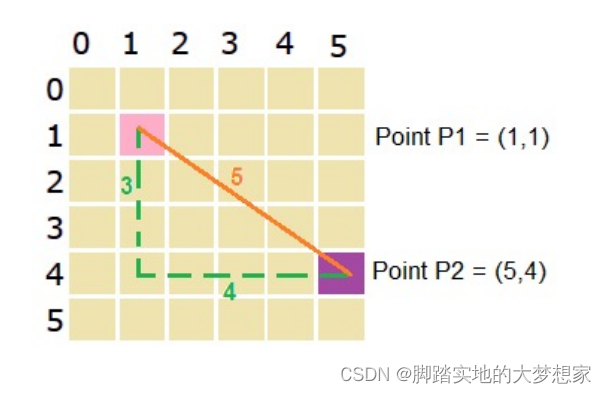
(c)方法属性minkowski (self, x, y, p)：计算两点x和y之间的闵可夫斯基距离，p为非负整数，用p=0情形表示切比雪夫距离。由此定义的距离称为p-闵氏距离，其数学定义如下：

(d)方法属性farthestpoint(self, p)：找出离中心点p-闵氏距离最远的点，返回在self.points中的下标以及最大距离。

(e)方法属性farthest2points(self, p)：找出点集self.points中p-闵氏距离最远的两点，返回两点在self.points中的下标及其最大距离。

要求

接下来，实例化类HDPoints，利用random模块，随机产生至少50个高维空间数据点，样本点的维度至少在5以上，且每个分量取值服从区间[0,1]上的均匀分布。同时，随机产生一个0~5之间的一个非负整数，赋值传递给p-闵氏距离函数中的参数p，对HDPoints实例对象的全部自定义方法属性（即centerpoint()、minkowski()、farthestpoint()和farthest2points()）进行功能测试。

代码

import numpy as npclass HDPoints(object):def __init__(self,list_HDPoints):self.points=list_HDPointsdef centerpoint(self):# 转化为高维数组,数组要求长度一致m=np.array(self.points)return sum(m) / len(m)def minkowski (self, x, y, p):if (p==0):p=1return sum([abs(x - y) ** p for x, y in zip(x, y)])**(1/p)def farthestpoint(self, p):centerPoint=self.centerpoint()list_instance=[self.minkowski(centerPoint,i,p)for i in self.points]max1=max(list_instance)return list_instance.index(max1),max1def farthest2points(self, p):max=0l1,l2=[],[]for i in self.points:for j in self.points[self.points.index(i)+1::]:if self.minkowski(i,j,p)>max:max=self.minkowski(i,j,p)l1,l2=i,jreturn max,self.points.index(l1),self.points.index(l2)#产生50个高维点
a=np.random.uniform(0,5,(50,5))
m=[]
for i in a:m1=[]for j in i:m1.append(int(j))m.append(m1)
print(m)
HD_Point=HDPoints(m)print("中心点是:",HD_Point.centerpoint())
print("两点之间的闵可夫斯基距离是:",HD_Point.minkowski([3,4,5,6],[2,3,4,5],4))
print("当p=5时,离中心点距离最远的点和下标是:",HD_Point.farthestpoint(5))
print("当p=5时，距离最远的两个点下标和距离是:",HD_Point.farthest2points(5))