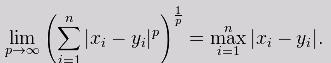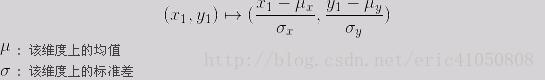在深度学习以及图像搜索中，经常要对特征值进行比对，得到特征的相似度，常见的特征值比对方法有汉明距离、余弦距离、欧式距离、曼哈顿距离、切比雪夫距离、闵可夫斯基距离、马氏距离等，下面对各种比对方法分别进行介绍。

目录

1汉明距离

2余弦相似度

3欧式距离

4曼哈顿距离

5切比雪夫距离

6闵可夫斯基距离

7马氏距离

1汉明距离

汉明距离/Hamming Distance也能用来计算两个向量的相似度；即通过比较向量每一位是否相同，若不同则汉明距离加1，这样得到汉明距离。向量相似度越高，对应的汉明距离越小。如10001001和10110001有3位不同。

2余弦相似度

余弦相似度是利用两个向量之间的夹角的余弦值来衡量两个向量之间的余弦相似度。两个向量越相似夹角越小，余弦值越接近1。

在n维空间中，对于向量A=(a1,a2,...an),B=(b1,b2,...,bn)，其余弦值为：

 

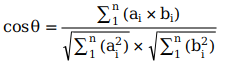
3欧式距离

欧式距离/Euclidean Distance即n维空间中两个点之间的实际距离。已知两个点A=(a1,a2,...an),B=(b1,b2,...,bn)，则AB间的距离为：

 

同样可以利用欧式距离计算图像的相似度，欧式距离越小相似度越大。

4曼哈顿距离

对于一个具有正南正北、正东正西方向规则布局的城镇街道，从一点到达另一点的距离正是在南北方向上旅行的距离加上在东西方向上旅行的距离，因此，曼哈顿距离又称为出租车距离。

在n维空间中，对于向量A=(a1,a2,...an),B=(b1,b2,...,bn)，曼哈顿距离为：

 

5切比雪夫距离

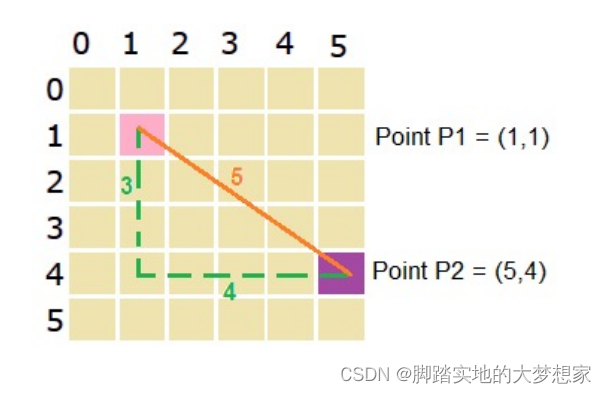
切比雪夫距离起源于国际象棋中国王的走法，国际象棋中国王每次只能往周围的8格中走一步，那么如果要从棋盘中A格(x1, y1)走到B格(x2, y2)最少需要走几步？你会发现最少步数总是max(| x2-x1 |,| y2-y1|) 步。有一种类似的一种距离度量方法叫切比雪夫距离。

    

        若将国际象棋棋盘放在二维直角座标系中，格子的边长定义为1，座标的x轴及y轴和棋盘方格平行，原点恰落在某一格的中心点，则王从一个位置走到其他位置需要的步数恰为二个位置的切比雪夫距离，因此切比雪夫距离也称为棋盘距离。例如位置F6和位置E2的切比雪夫距离为4。任何一个不在棋盘边缘的位置，和周围八个位置的切比雪夫距离都是1。

        两个n维向量A=(a1,a2,...an),B=(b1,b2,...,bn)间的切比雪夫距离：

  

6闵可夫斯基距离

假设空间中的两个点坐标分别为，A=(a1,a2,...an),B=(b1,b2,...,bn)，则闵可夫斯基距离的计算公式为：

 

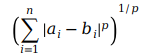
该距离最常用的p是2和1，当p=2时变成欧式距离，当p=1时变成曼哈顿距离。

当p趋近于无穷大时，闵可夫斯基距离转化成切比雪夫距离，

  

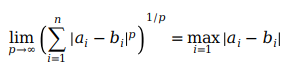
7马氏距离

马氏距离的引出：

   

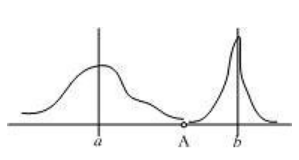
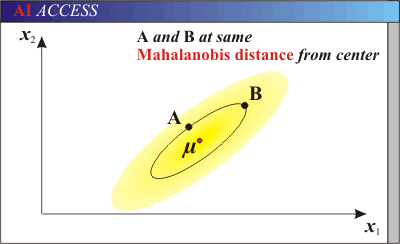
        上图有两个正态分布的总体，它们的均值分别为a和b，但方差不一样，则图中的A点离哪个总体更近？或者说A有更大的概率属于谁？显然，A离左边的更近，A属于左边总体的概率更大，尽管A与a的欧式距离远一些。这就是马氏距离的直观解释。

        马氏距离是基于样本分布的一种距离。物理意义就是在规范化的主成分空间中的欧氏距离。所谓规范化的主成分空间就是利用主成分分析对一些数据进行主成分分解。再对所有主成分分解轴做归一化，形成新的坐标轴。由这些坐标轴张成的空间就是规范化的主成分空间。

  

定义：有M个样本向量X1~Xm，协方差矩阵记为S，均值记为向量μ，则其中样本向量X到μ的马氏距离表示为：

  

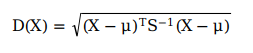
向量Xi和Xj之间的马氏距离定义为：

  

如果协方差矩阵是单位矩阵，则Xi与Xj之间的马氏距离等于他们的欧氏距离：

 

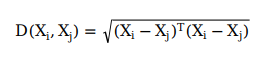
马氏距离的特点：

量纲无关，排除变量之间的相关性的干扰；

马氏距离的计算是建立在总体样本的基础上的，如果拿同样的两个样本，放入两个不同的总体中，最后计算得出的两个样本间的马氏距离通常是不相同的，除非这两个总体的协方差矩阵碰巧相同；

计算马氏距离过程中，要求总体样本数大于样本的维数，否则得到的总体样本协方差矩阵逆矩阵不存在，这种情况下，用欧式距离计算即可。