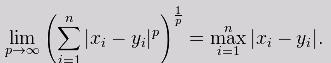这里写目录标题
- 闵可夫斯基距离
- 曼哈顿距离
- 欧几里得距离
- e . g . e.g. e.g. 曼哈顿距离与欧几里得距离
三种距离计算算法

闵可夫斯基距离
闵可夫斯基距离(Minkowski Dis) ,是 曼哈顿距离(Manhattan Dis) 与 欧几里得距离(Euclidean Dis) 的一般形式。一般不常直接使用。
当 N = 1 N=1 N=1 时,闵可夫斯基距离转化为曼哈顿距离;
当 N = 2 N=2 N=2 时,闵可夫斯基距离转化为欧几里得距离。
本笔记将主要围绕曼哈顿距离以及欧几里得距离。
曼哈顿距离
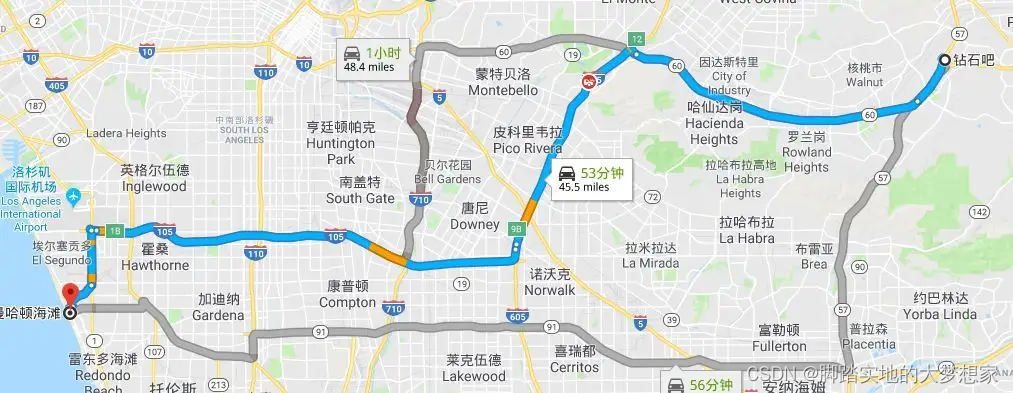
Manhattan Distance 曼哈顿距离,是闵可夫斯基所创,又称为出租车距离。主要应用场景为城市交通。在大多数城市,两个点之间的距离很难做到直线抵达。
d ( x i , x j ) = ∣ x i 1 , x j 1 ∣ + ∣ x i p , x j p ∣ + . . . + ∣ x i p , x j p ∣ d(x_i, x_j)=|x_{i1}, x_{j1}|+|x_{ip}, x_{jp}|+...+|x_{ip}, x_{jp}| d(xi,xj)=∣xi1,xj1∣+∣xip,xjp∣+...+∣xip,xjp∣
欧几里得距离
Euclidean Distance 欧几里得距离,主要应用场景为数学以及现在贼火的计算机视觉与图像处理领域。
d ( x i , x j ) = ∣ x i 1 , x j 1 ∣ 2 + ∣ x i p , x j p ∣ 2 + . . . + ∣ x i p , x j p ∣ 2 d(x_i,x_j)=\sqrt {|x_{i1}, x_{j1}|^2+|x_{ip}, x_{jp}|^2+...+|x_{ip}, x_{jp}|^2} d(xi,xj)=∣xi1,xj1∣2+∣xip,xjp∣2+...+∣xip,xjp∣2
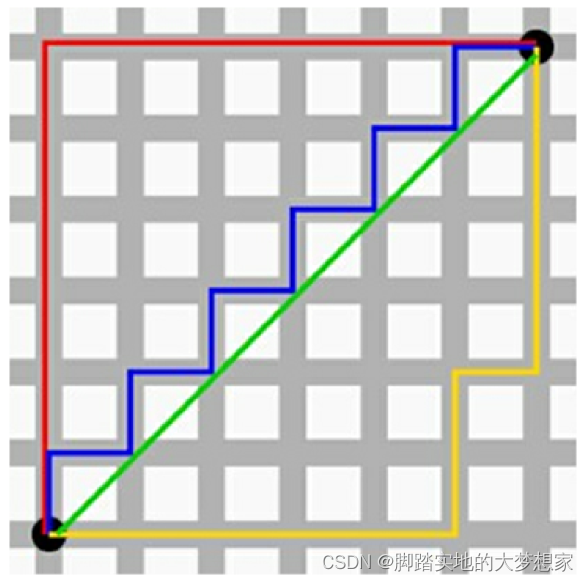
其中只有绿色的路径为欧几里得距离,其他全部为曼哈顿距离。
e . g . e.g. e.g. 曼哈顿距离与欧几里得距离
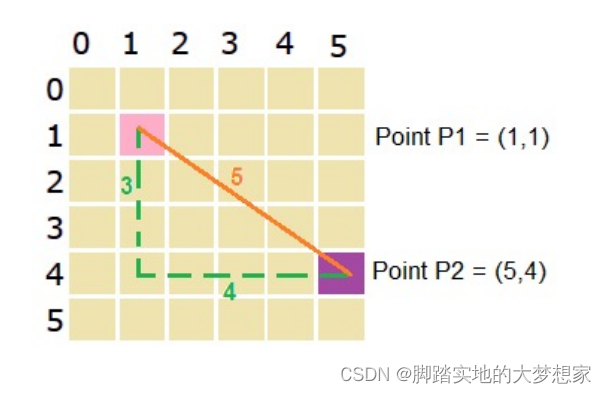
M a n h a t t a n D i s t a n c e = ∣ 5 − 1 ∣ + ∣ 4 − 1 ∣ = 7 Manhattan Distance = |5-1|+|4-1|=7 ManhattanDistance=∣5−1∣+∣4−1∣=7
E u c l i d e a n D i s t a n c e = ( 5 − 1 ) 2 + ( 4 − 1 ) 2 = 5 Euclidean Distance = \sqrt {(5-1)^2+(4-1)^2}=5 EuclideanDistance=(5−1)2+(4−1)2=5
2022.10.9 于 海韵轩
2022.11.4 修改补充