1.排序
-快速排序(先排序后递归)
一.找某一个数为基点(假设为x)
二.将这个数分为|--------<=x---------|-------->=x-------|
x
三.然后递归,x左,右两侧分别排序
四.后输出
核心代码:
void quick_sort(int q[], int l, int r)
{if (l >= r) return;int i = l - 1, j = r + 1, x = q[l + r >> 1];while (i < j){do i ++ ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i], q[j]);}quick_sort(q, l, j), quick_sort(q, j + 1, r);
}
-归并排序
一.找一组数的中间值(数组里的)
二.将其分为左,右半边
|-------|-------|
left mid right
两边最小值比较
3.合并得结果
核心代码:
void merge_sort(int q[], int l, int r){if (l >= r)return;int mid = l + r >> 1;merge_sort(q, l, mid);merge_sort(q, mid + 1, r);int k = 0, i = l, j = mid + 1;while (i <= mid && j <= r)if (q[i] <= q[j]) tmp[k ++ ] = q[i ++ ];else tmp[k ++ ] = q[j ++ ];while (i <= mid) tmp[k ++ ] = q[i ++ ];while (j <= r) tmp[k ++ ] = q[j ++ ];for (i = l, j = 0; i <= r; i ++, j ++ )q[i] = tmp[j];}2.二分查找
一.mid=r+l+1>>1;
1 .true [mid,r] l=mid
2 .false [l,mid] r=mid-1
二.mid=l+r>>1;
1.true [l,mid] r=mid
2.false [mid+1,r] l=mid+1
核心代码:
bool check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用:int bsearch_1(int l, int r){while (l < r){int mid = l + r >> 1;if (check(mid))r = mid; // check()判断mid是否满足性质elsel = mid + 1;}return l;}// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用:int bsearch_2(int l, int r){while (l < r){int mid = l + r + 1 >> 1;if (check(mid))l = mid;elser = mid - 1;}return l;3.高精度
《1》加法
A1 A2 A3
+ B1 B2
-----------------------
C1 C2 C3
核心代码:
vector<int> add(vector<int> &A, vector<int> &B){if (A.size() < B.size())return add(B, A);vector<int> C;int t = 0;for (int i = 0; i < A.size(); i ++ ){t += A[i];if (i < B.size()) t += B[i];C.push_back(t % 10);t /= 10;}if (t)C.push_back(t);return C;}2.减法
A1 A2 A3
— B1 B2
-----------------------
C1 C2 C3
核心代码:
// C = A - B, 满足A >= B, A >= 0, B >= 0vector<int> sub(vector<int> &A, vector<int> &B){vector<int> C;for (int i = 0, t = 0; i < A.size(); i ++ ){t = A[i] - t;if (i < B.size())t -= B[i];C.push_back((t + 10) % 10);if (t < 0)t = 1;else t = 0;}while (C.size() > 1 && C.back() == 0)C.pop_back();return C;}3.高精度乘法
A1 A2 A3
x B1 B2
---------------------
C1 C2 C3
核心代码:
vector<int> mul(vector<int> &A, int b){vector<int> C;int t = 0;for (int i = 0; i < A.size() || t; i ++ ){if (i < A.size())t += A[i] * b;C.push_back(t % 10);t /= 10;}while (C.size() > 1 && C.back() == 0)C.pop_back();return C;}4.除法
// A / b = C ... r, A >= 0, b > 0vector<int> div(vector<int> &A, int b, int &r){vector<int> C;r = 0;for (int i = A.size() - 1; i >= 0; i -- ){r = r * 10 + A[i];C.push_back(r / b);r %= b;}reverse(C.begin(), C.end());while (C.size() > 1 && C.back() == 0)C.pop_back();return C;}4.前缀与差分
一.一维前缀和
核心代码:
for(int i=1;i<=n;i++)s[i]=s[i-1]+a[i];二.二维前缀和
核心代码:
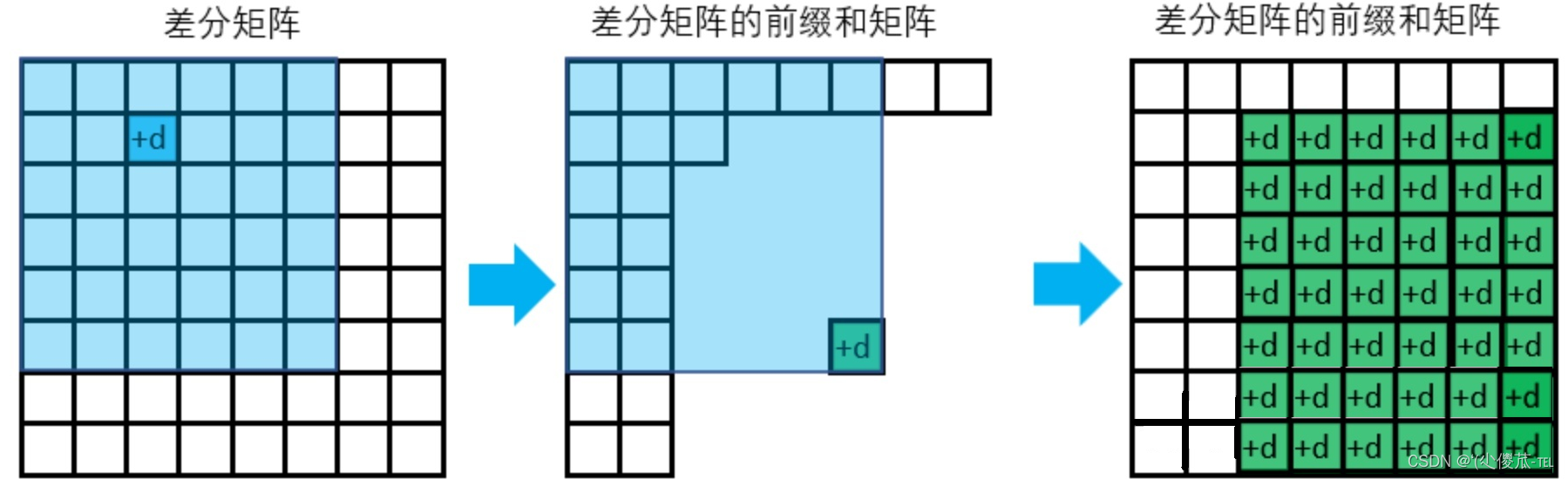
for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)s[i][j]=s[i-1][j]+s[i][j-1]-s[i-1][j-1]+a[i][j];三.差分(前缀和的逆运算)
构造使得a成为b的前缀和,b则称为a 的差分。
一.一维差分
核心代码:
void insert(int l,int r,int c){b[l]+=c;b[r+1]-=c;//[l,r]区间内加c,r+1不需要+c,所以减去c}二.二维差分
核心代码:
void insert (int x1,int y1,int x2 int y2,int c){b[x1][y1]+=c;b[x2+1][y1]-=c;b[x1][y2+1]-=c;b[x2+1][y2+1]+=c;}5.双指针算法
核心代码:
for (int i = 0, j = 0; i < n; i ++ ){while (j < i && check(i, j))j ++ ;}6.位运算

参考百度图片
7.离散化
例如 a[i] 1 3 100 2000
离散化后 0 1 2 3----->这个过程叫离散化
核心代码:
vector<int> alls; // 存储所有待离散化的值sort(alls.begin(), alls.end()); // 将所有值排序alls.erase(unique(alls.begin(), alls.end()), alls.end()); // 去掉重复元素// 二分求出x对应的离散化的值int find(int x) // 找到第一个大于等于x的位置{int l = 0, r = alls.size() - 1;while (l < r){int mid = l + r >> 1;if (alls[mid] >= x) r = mid;else l = mid + 1;}return r + 1; // 映射到1, 2, ...n}8.区间合并
例如:
|——| |———| |——| |——| |——|
1 2 2 3 4 5 6 7 8 8 9
|————| |——| |——|
1 4 5 6 7 9
核心代码:
// 将所有存在交集的区间合并void merge(vector<PII> &segs){vector<PII> res;sort(segs.begin(), segs.end());int st = -2e9, ed = -2e9;for (auto seg : segs)if (ed < seg.first){if (st != -2e9) res.push_back({st, ed});st = seg.first, ed = seg.second;}else ed = max(ed, seg.second);if (st != -2e9) res.push_back({st, ed});segs = res;