来源: bilibili数据结构与算法基础(青岛大学-王卓)
1.2 基本概念和术语
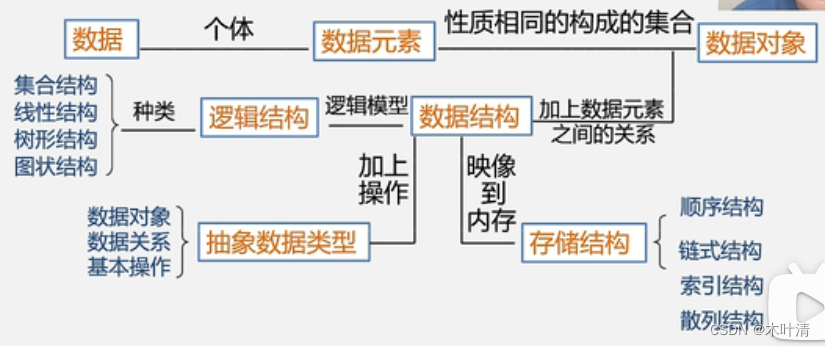
数据结构
数据元素之间的关系称为结构,数据结构是相互之间存在一种或多种特定关系的数据元素的集合。
数据结构的两个层次:逻辑结构和物理结构
逻辑结构:描述数据元素之间的逻辑关系,与数据的存储无关,独立于计算机,是数据结构的抽象
物理结构(存储结构):数据元素及其关系在计算机内存中的存储方式,是数据结构的实现
逻辑结构的种类
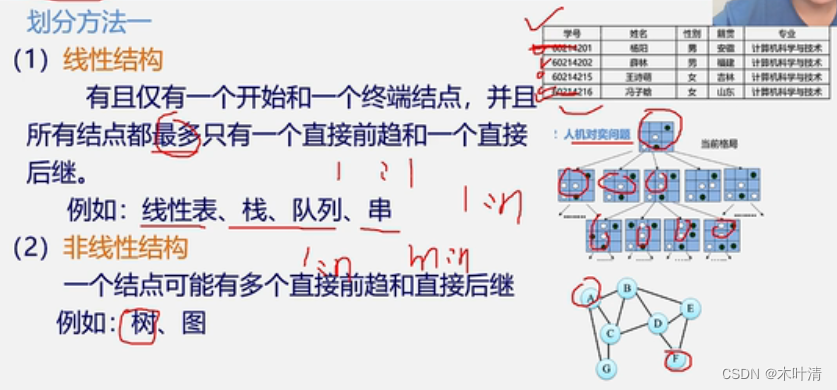
划分方式二——四种基本逻辑结构
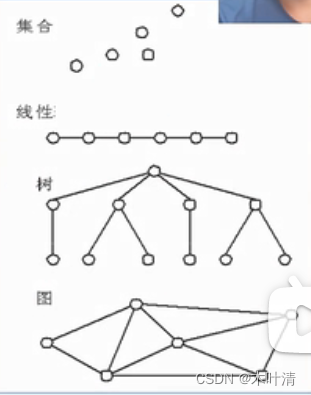
线性结构(一对一)、树(一对多)、图(多对多)
存储结构的种类: 顺序,链式,索引,散列


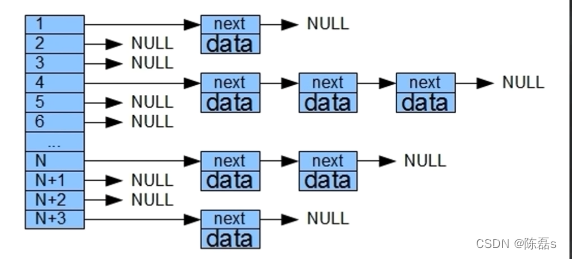
索引存储结构:存储结点信息时,建立附加的索引表,例如通讯录中根据首字母查找联系人
散列存储结构:根据结点的关键字直接计算出结点的存储地址
1.3 基本概念与术语
算法的时间复杂度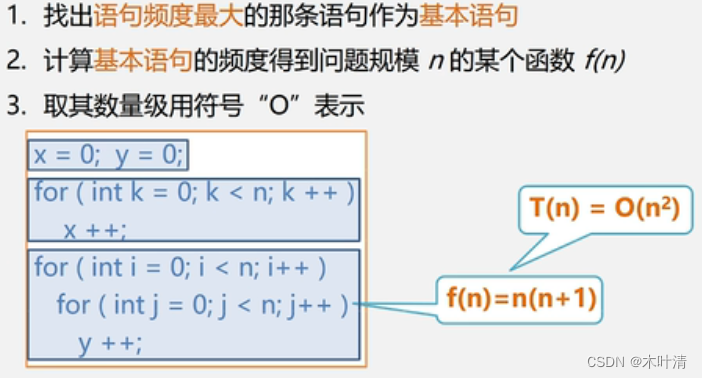




时间复杂度T(n)按数量级递增顺序为:

算法的空间复杂度

2.1 线性表的定义和特点

同一线性表中的元素必有相同特性,数据元素之间的关系是线性的。
2.4 线性表的顺序表示和实现
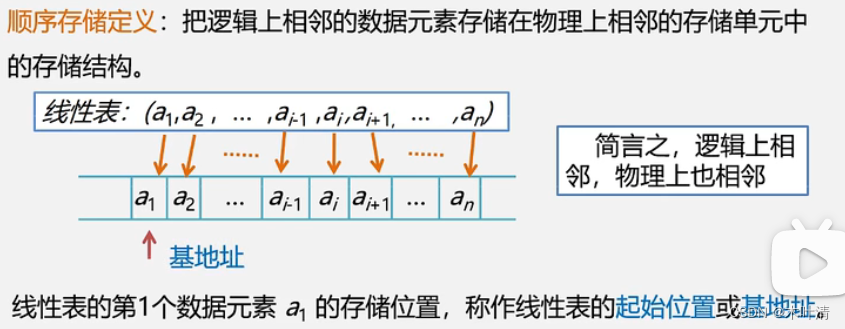
线性表顺序存储结构必须占用一片连续的存储空间。




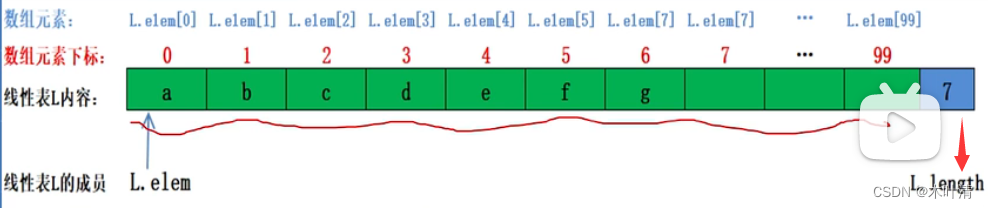
#define max 10000
#define true 1
#define false -1
#define OVERFLOW -2//顺序表类型
typedef int eletype;
typedef struct{eletype* data;int length;
}sqlist;//初始化
int initlist(sqlist& l){l.data = new eletype[max];l.length = 0;if (!l.data)exit(OVERFLOW);return true;
}
//销毁
void destroylist(sqlist& l){if (l.data)delete l.data;
}
//清空
void clearlist(sqlist& l){l.length = 0;
}
//在线性表第i个位置插入新元素e
int listinsert(sqlist& l, int i, eletype e){if (i<1 || i>l.length + 1)return false;if (l.length == max)return OVERFLOW;for (int j = l.length - 1; j >= i-1;j--)l.data[j + 1] = l.data[j];l.data[i - 1] = e;l.length++;return true;
}
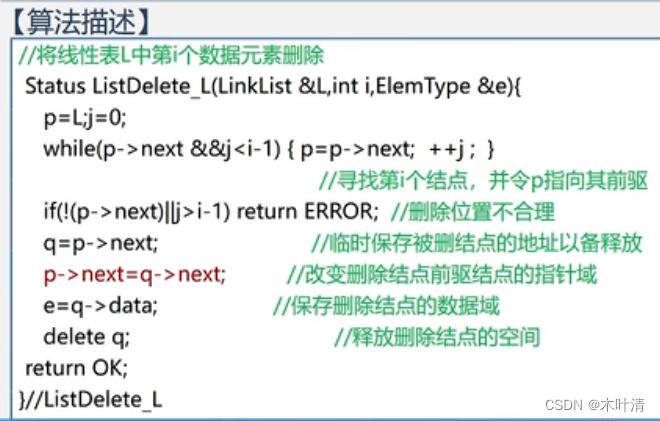
//删除第i个元素,返回删除元素的值
int listdelete(sqlist& l, int i){if (i<1 || i>l.length || l.length == 0)return false;for (int j = i; j <= l.length-1; j++)l.data[j-1] = l.data[j];l.length--;return true;
}
//顺序表是否为空
int isempty(sqlist& l){if (l.length == 0)return true;elsereturn false;
}
//返回顺序表长度
int getlength(sqlist& l){return l.length;
}
//查找与给定值相等的元素,返回该元素在表中的序号
int getlocation(sqlist& l, eletype e){for (int i = 0; i < l.length; i++){if (l.data[i] == e)return i + 1;}return false;
}
//将顺序表的第i个位置的元素返回给e
int getvalue(sqlist& l, int i, eletype& e){if (i<1 || i>l.length)return false;e = l.data[i - 1];return true;
}
void listshow(sqlist& l){for (int i = 0; i < l.length; i++)cout << l.data[i] << " ";cout << endl;
}顺序表查找、插入和删除算法的平均时间复杂度为O(n),顺序表操作算法的空间复杂度为O(1)
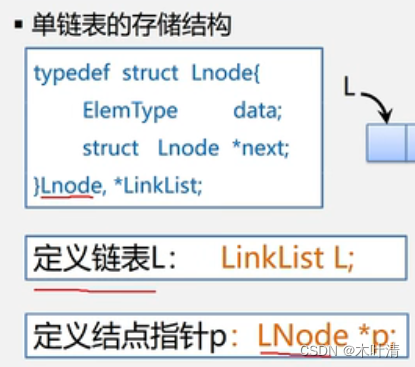
2.5 线性表的链式表示和实现
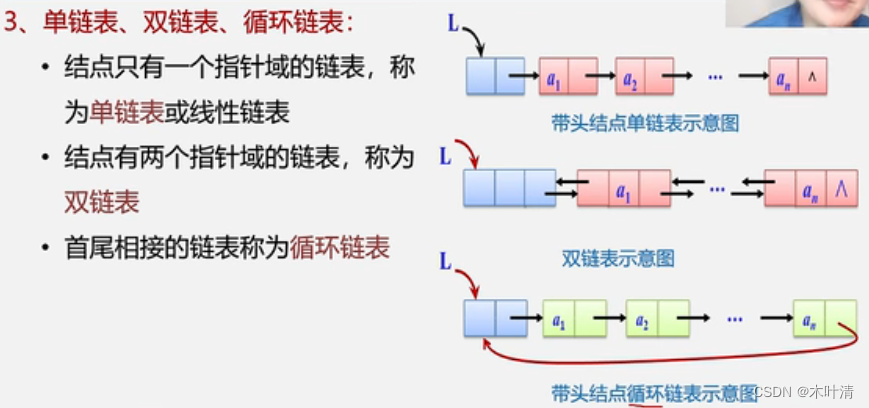
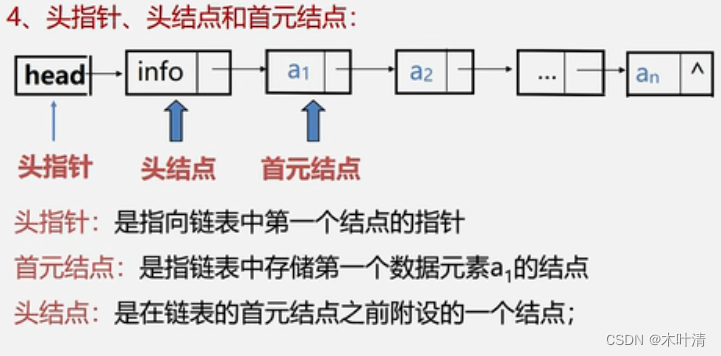
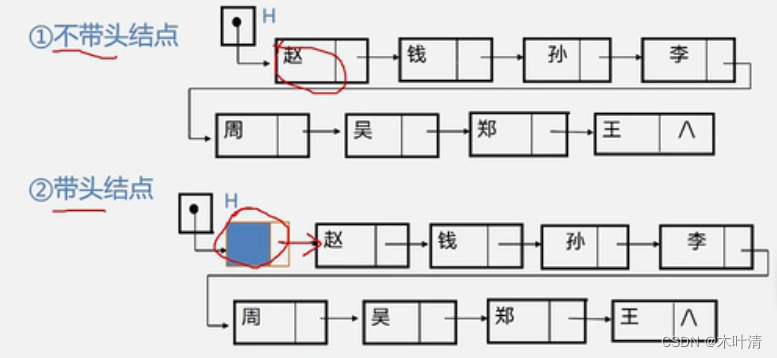
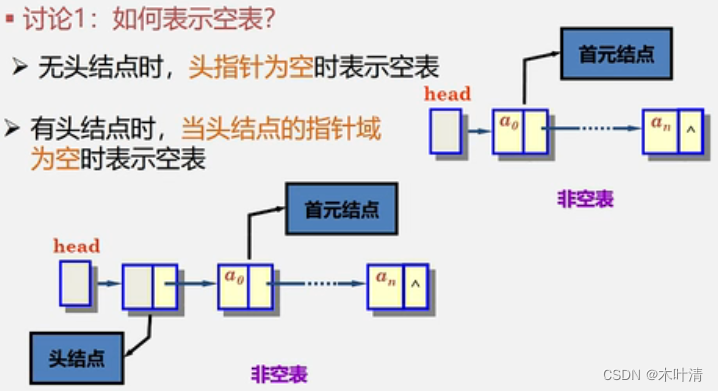

顺序表(数组)是随机存取,链表是顺序存取
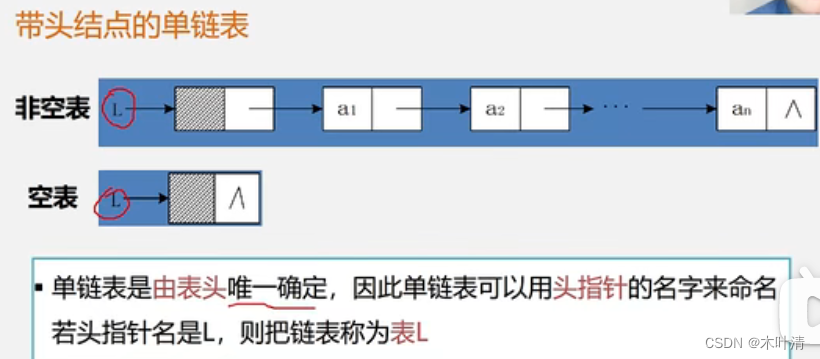
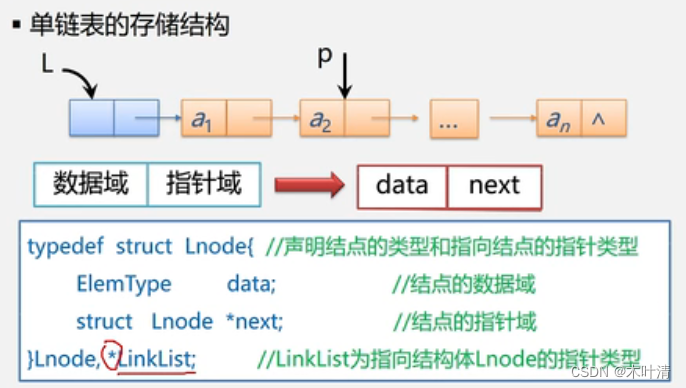
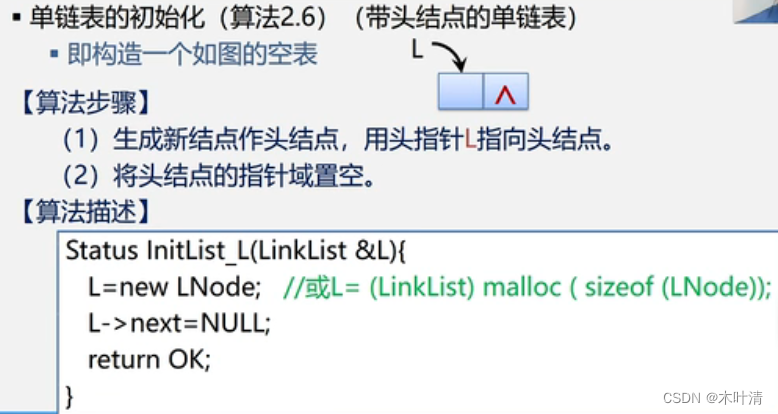

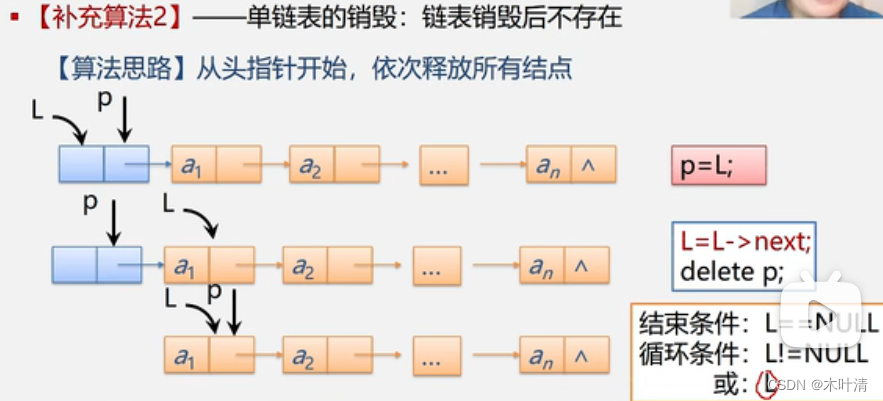
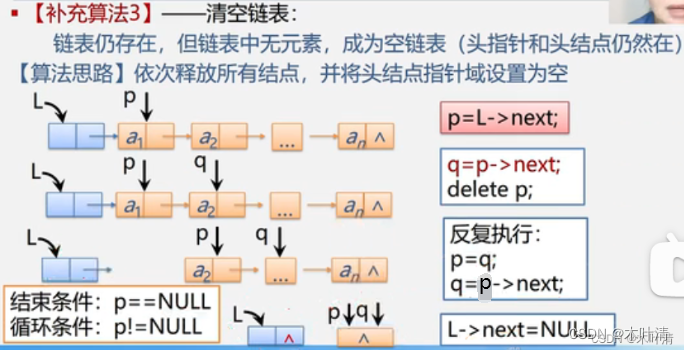
销毁单链表L:
Status DestroyList_L(LinkList &L){Lnode* p;while(L){p=L; //p指向头结点L=L->next;delete p;}return OK;
}

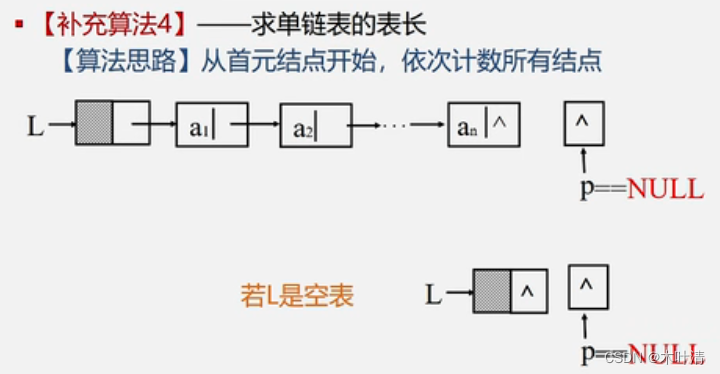
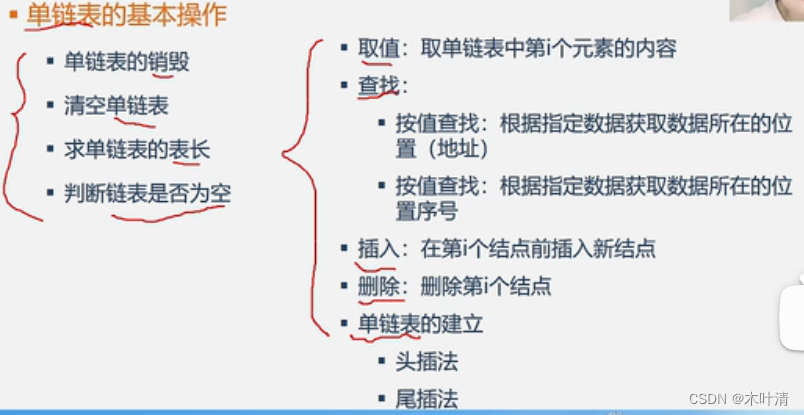
求单链表的表长:
int ListLength(LinkList L){Lnode* p;p=L->next;//p指向第一个结点i=0;while(p) //遍历单链表,统计结点数{i++;p=p->next;}return i;
}单链表取值操作:

如果p指向的结点为NULL( i 超出链表结点长度)或者 i=0,-1的情况出现,返回0
按值查找:1.返回值为e的数据元素地址;2.返回值为e的数据元素序号


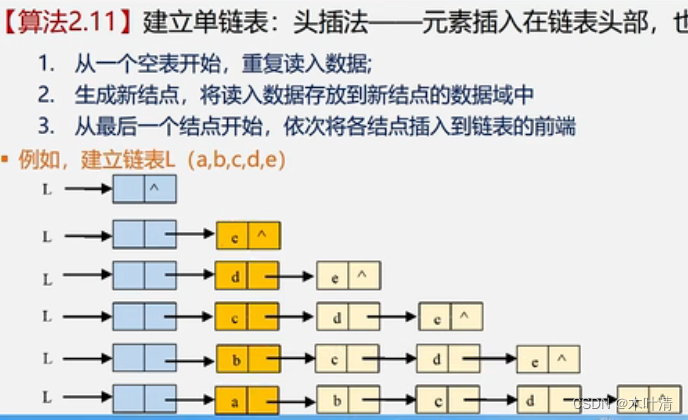
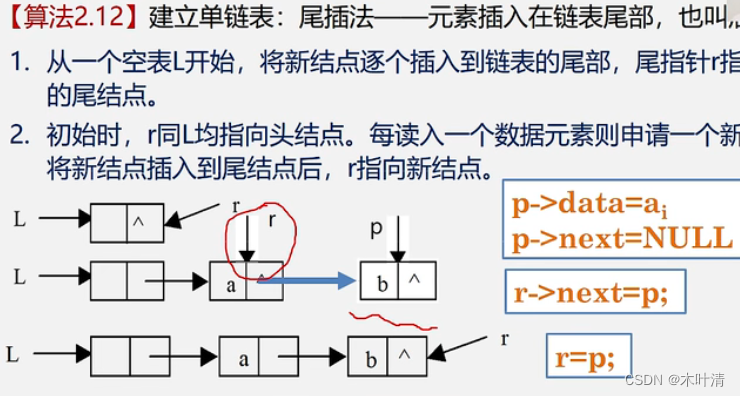
插入新结点:
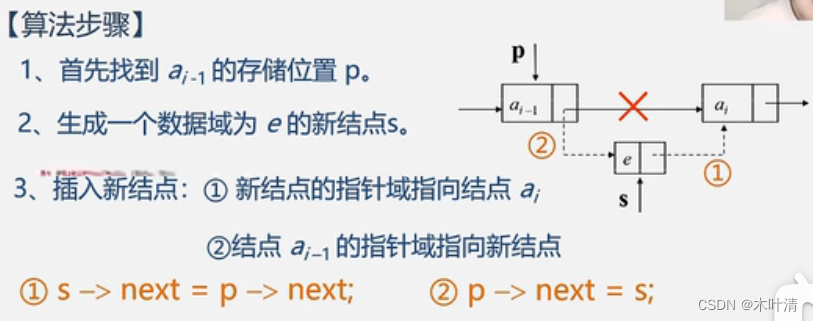

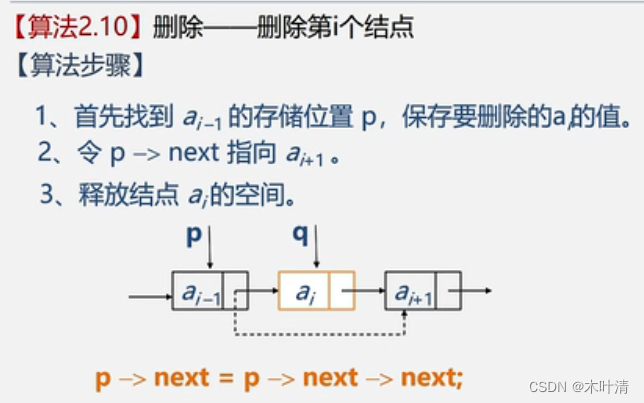



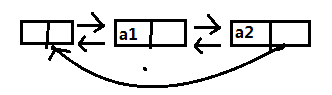
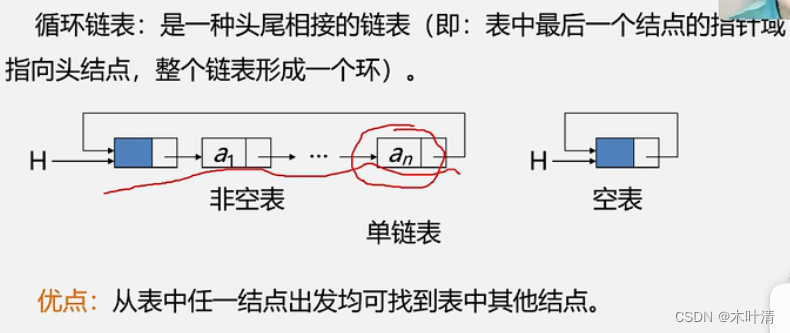
2.5.3 循环链表


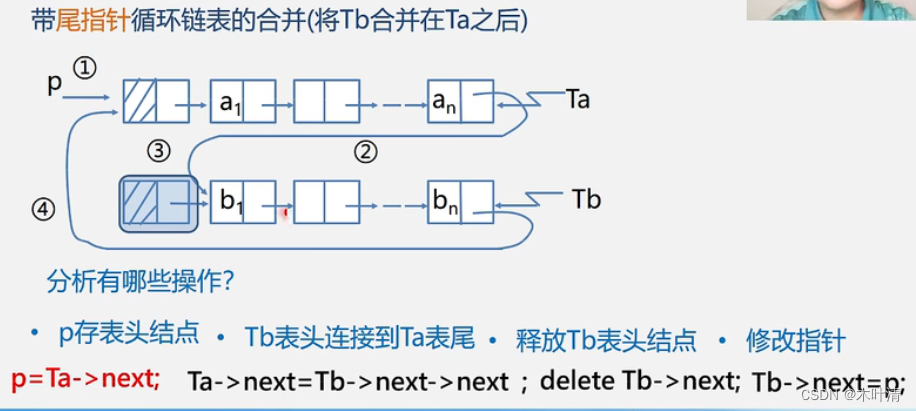
2.5.3 循环链表-两个链表合并

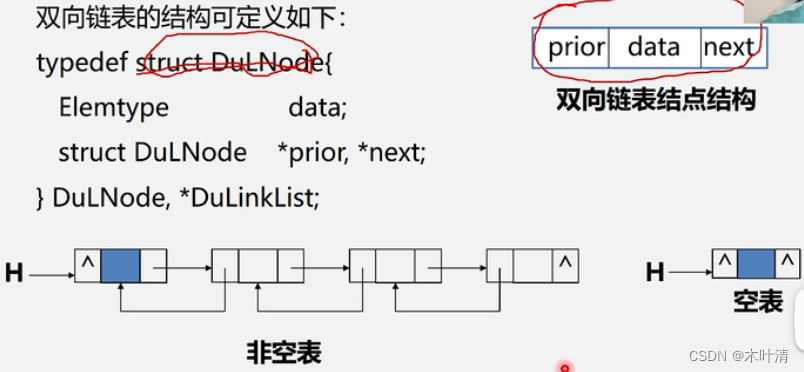
2.5.4 双向链表

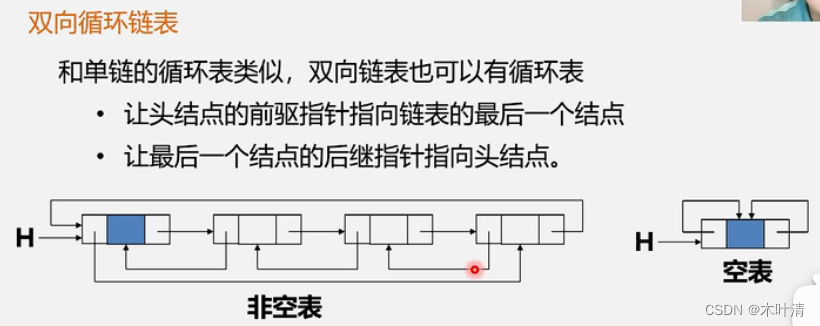

双向链表的插入

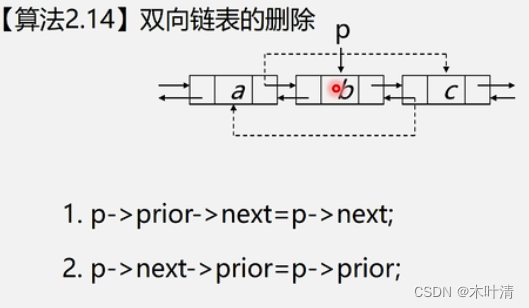
双向链表的删除
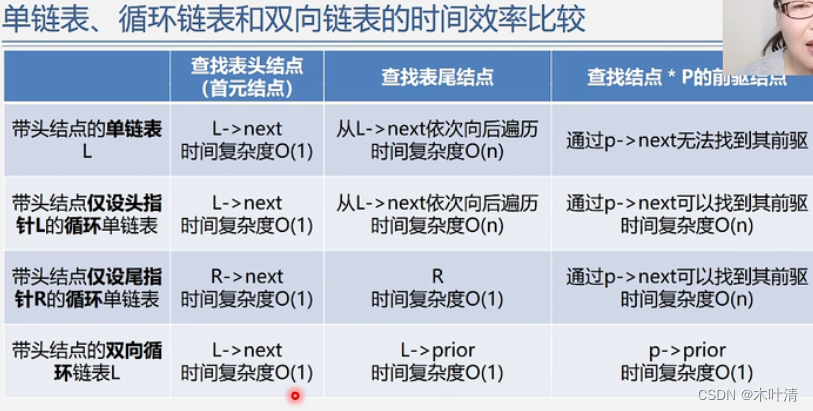
2.6 顺序表和链表的比较
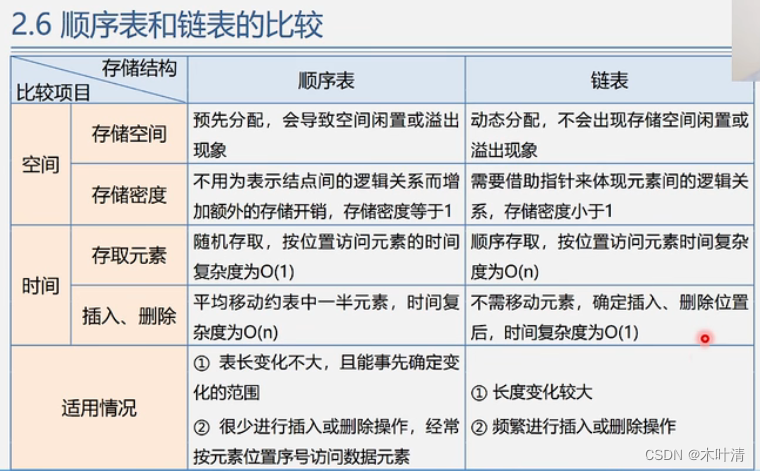

顺序表的存储密度=1,链表的存储密度<1,存储空间利用率较低
2.7 线性表的应用
线性表的合并

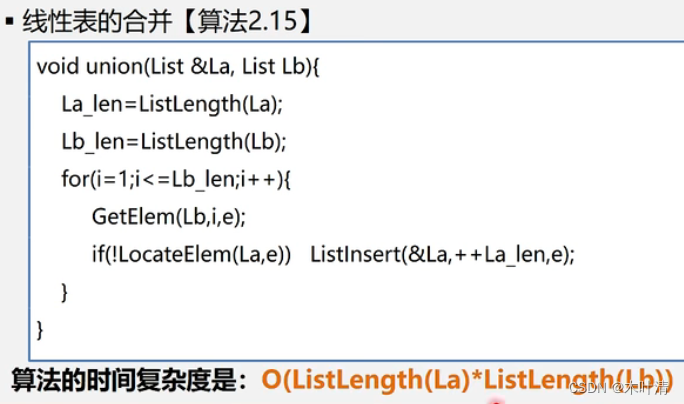
有序表的合并-用顺序表实现



有序表合并-用链表实现
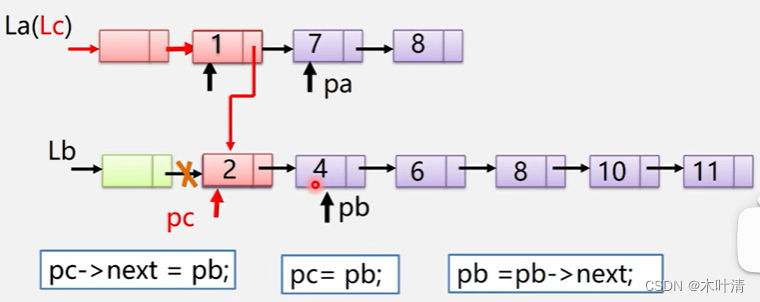
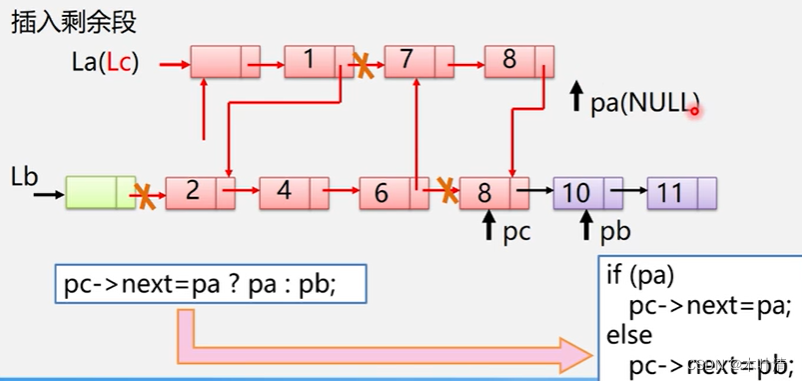

2.8 案例分析与实现
实现两个多项式相加
稀疏多项式的运算





3.1 栈和队列的定义和特点
栈只能在表尾插入和删除-后进先出,队列在队尾插入,在队头删除-先进先出

3.2 案例引入
进制转换
将十进制整数转换为其他进制数d,转换法则:除以d倒取余
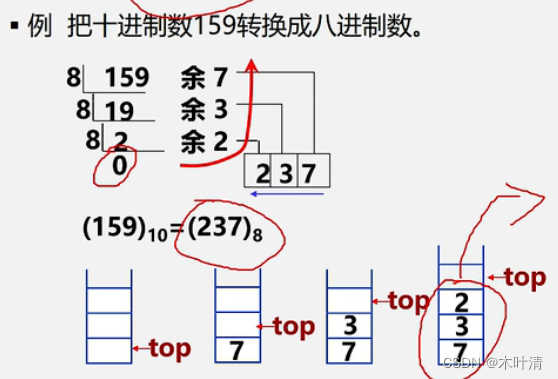
括号匹配的检验

表达式求值


舞伴问题

3.3 栈的表示和实现
顺序栈的表示和实现

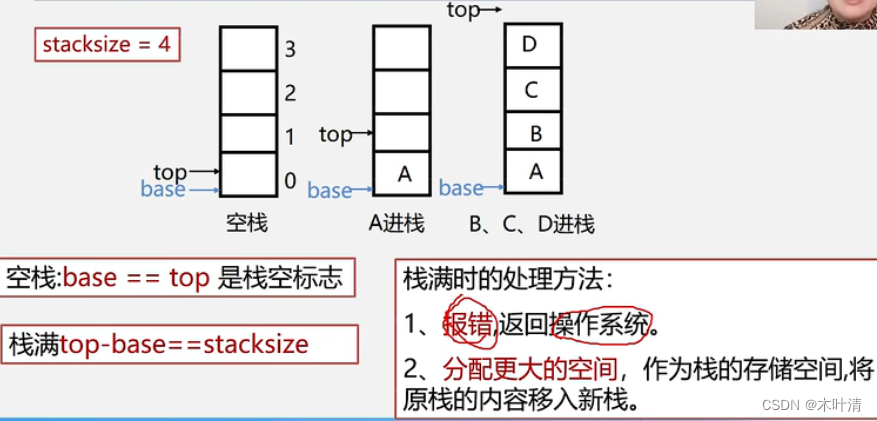
上溢(overflow):栈满还要压入元素;下溢(underflow):栈空还要弹出元素

初始化操作
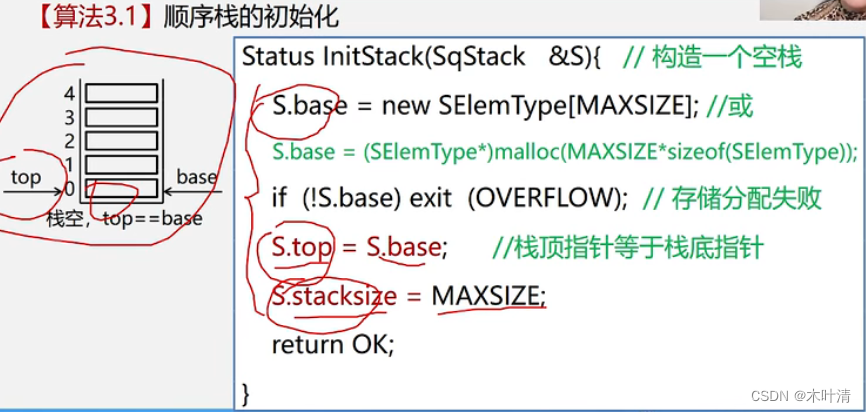
判断栈是否为空
求顺序栈的长度

清空顺序栈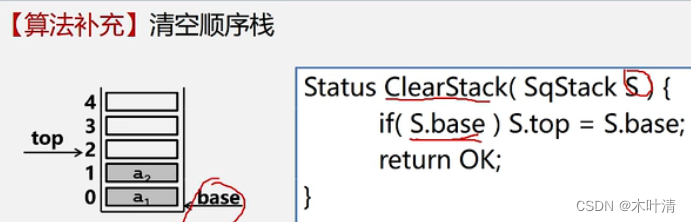
销毁顺序栈

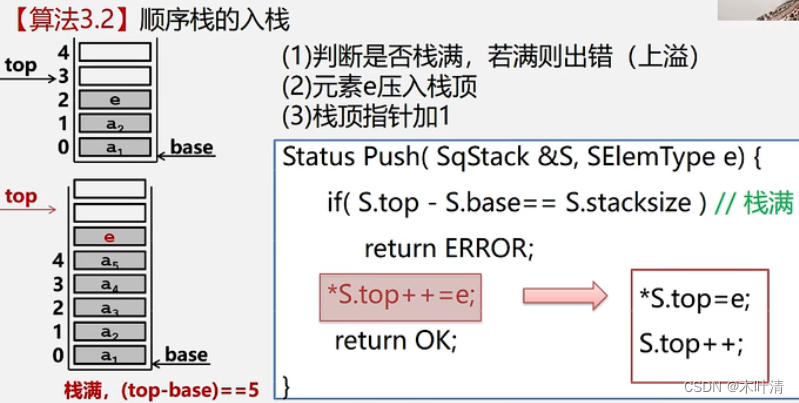
顺序栈的入栈
顺序栈的出栈

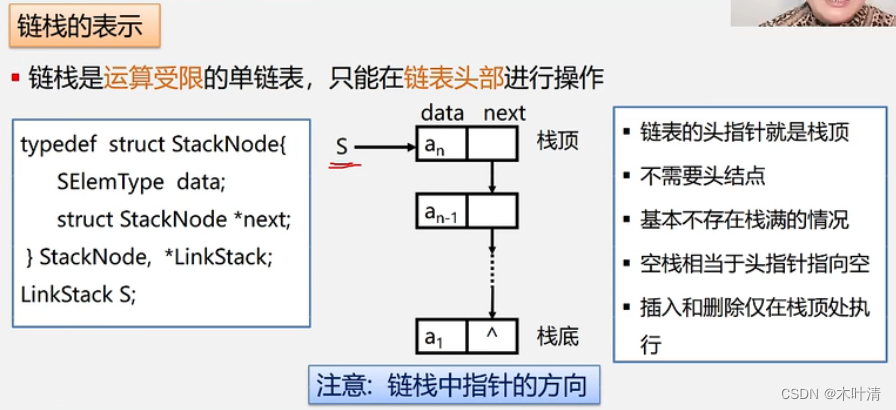
链栈的表示与实现
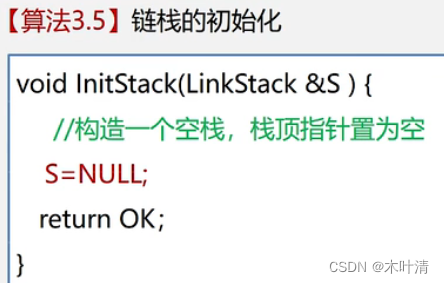
链栈的初始化
判断链栈是否为空

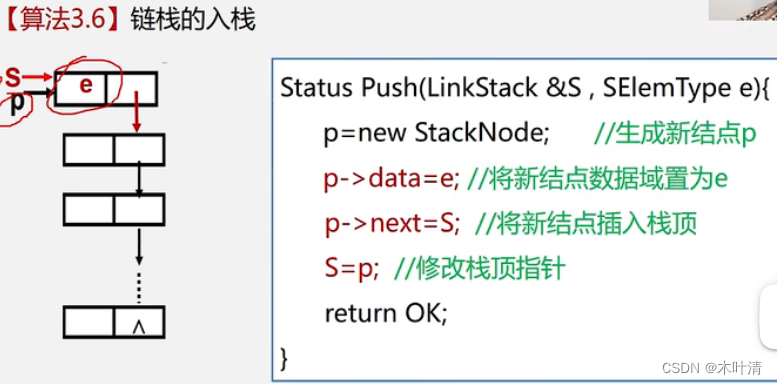
链栈的入栈
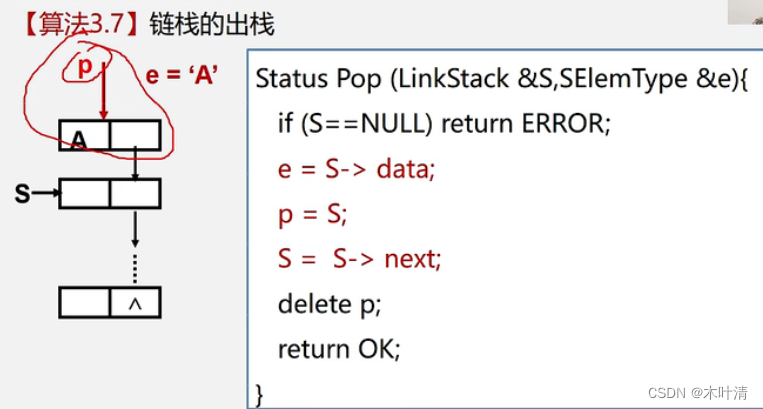
链栈的出栈
取栈顶元素

3.4 栈和递归
递归:一个过程直接或间接的调用自己
递归定义的数学函数

具有递归性质的数据结构
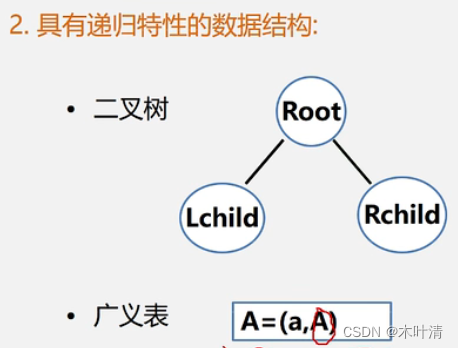

递归遵循——后调用先返回,要实现递归需要栈
3.5 队列的表示与实现
队列——头删尾插
队列的顺序表示

解决假溢出的方法——引入循环队列
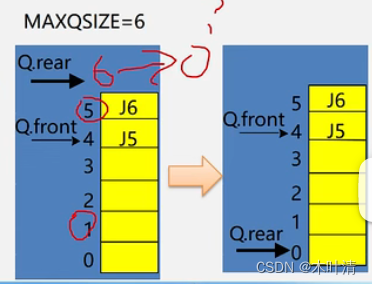

队空队满都为front==rear
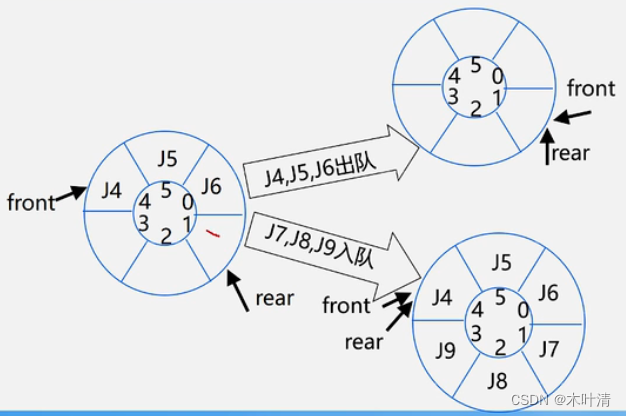
判断队空队满——少用一个元素空间

队列的初始化

求队列的长度
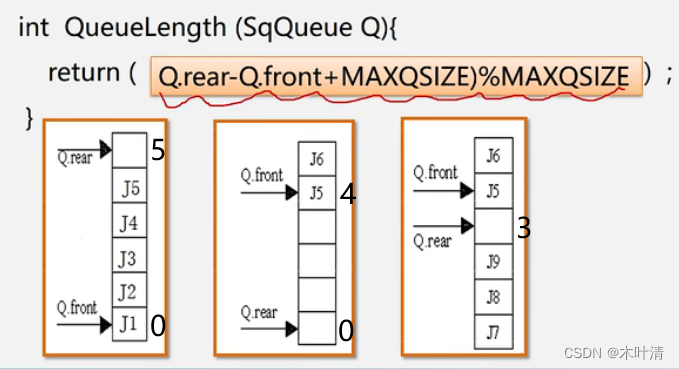
入队操作

出队操作

取队头元素

队列的链式表示和实现
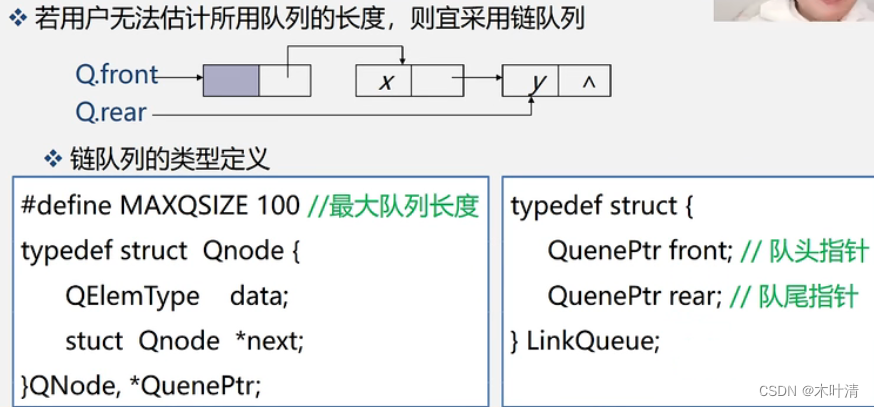

链队列初始化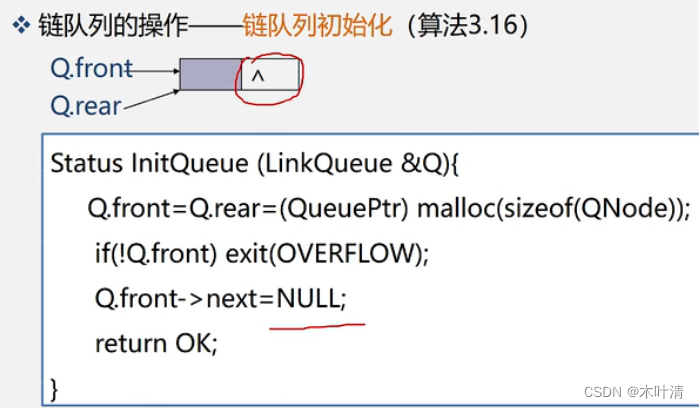
销毁链队列
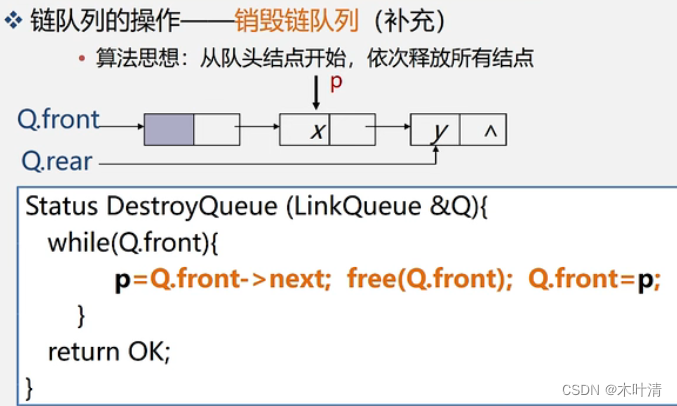
链队列入队

链队列出队

求链队列的队头元素

4.1 串的定义
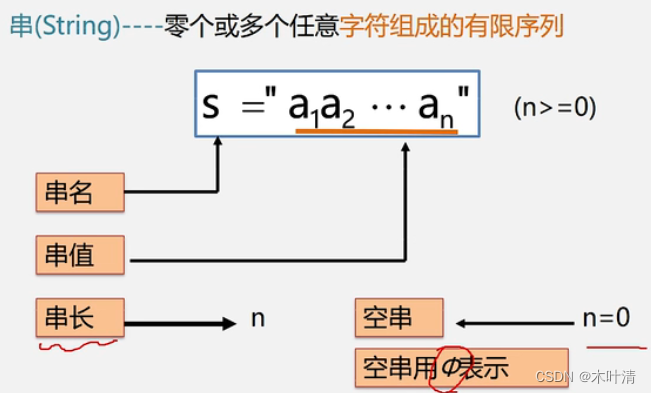

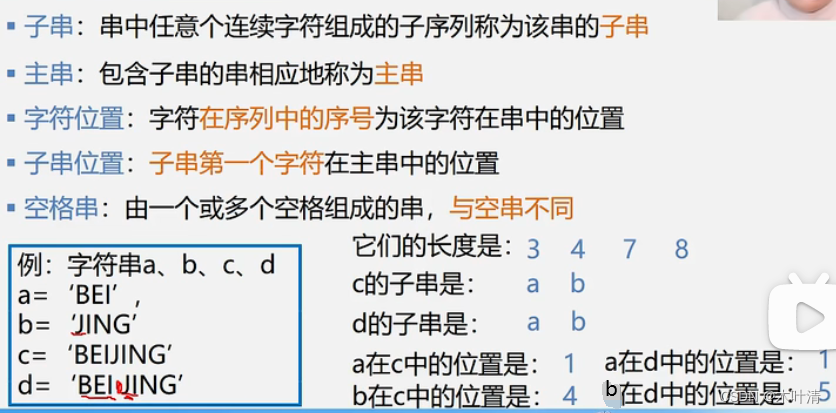

4.3 串的类型定义、存储结构及运算
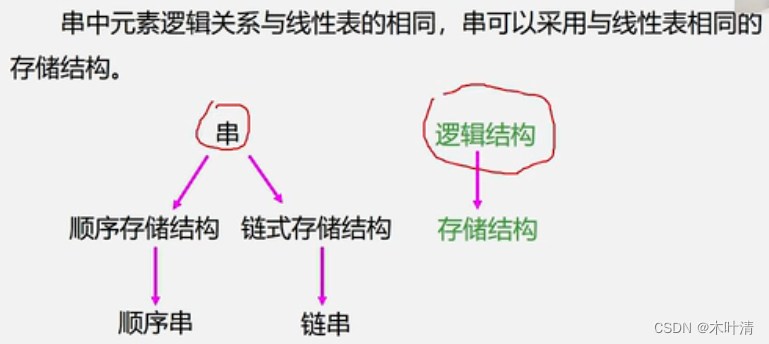


4.3.3 串的模式匹配算法

BF算法
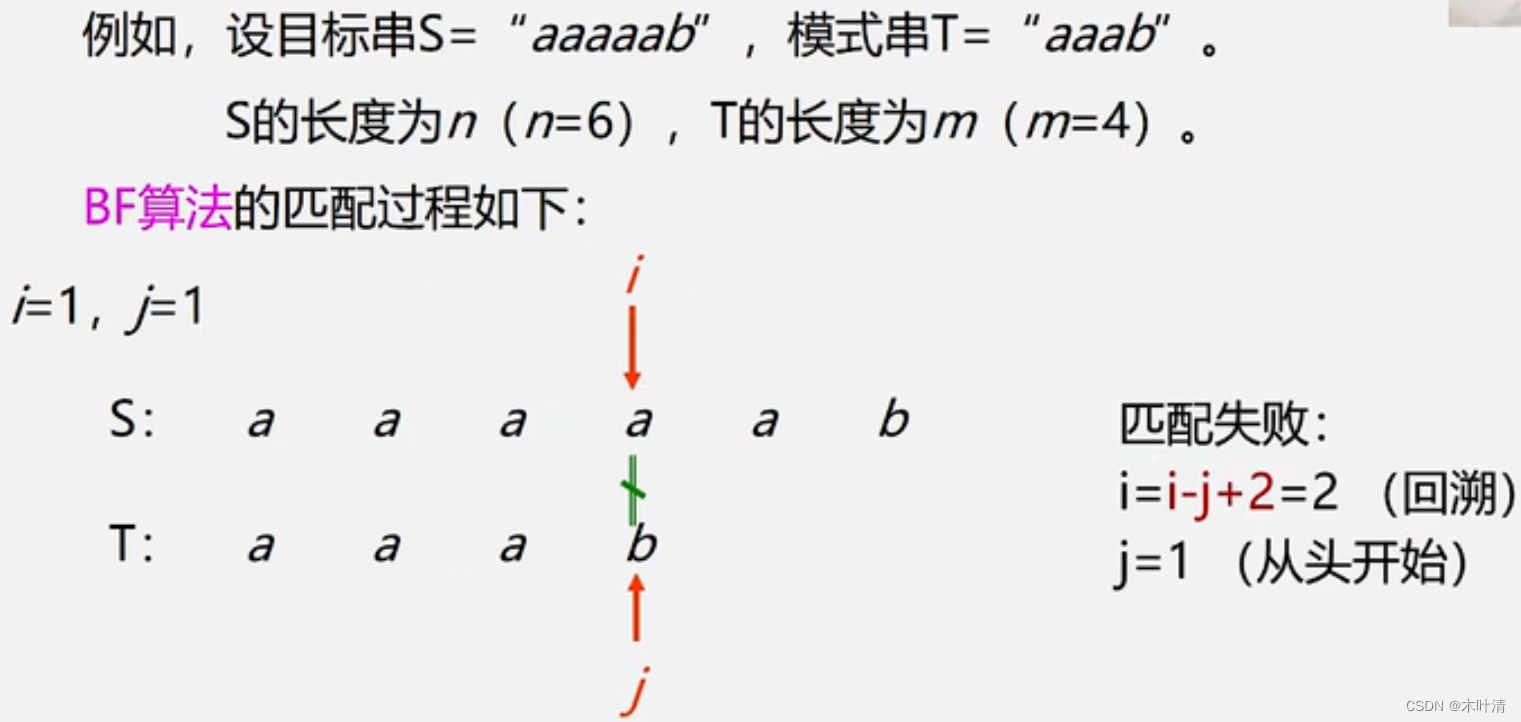
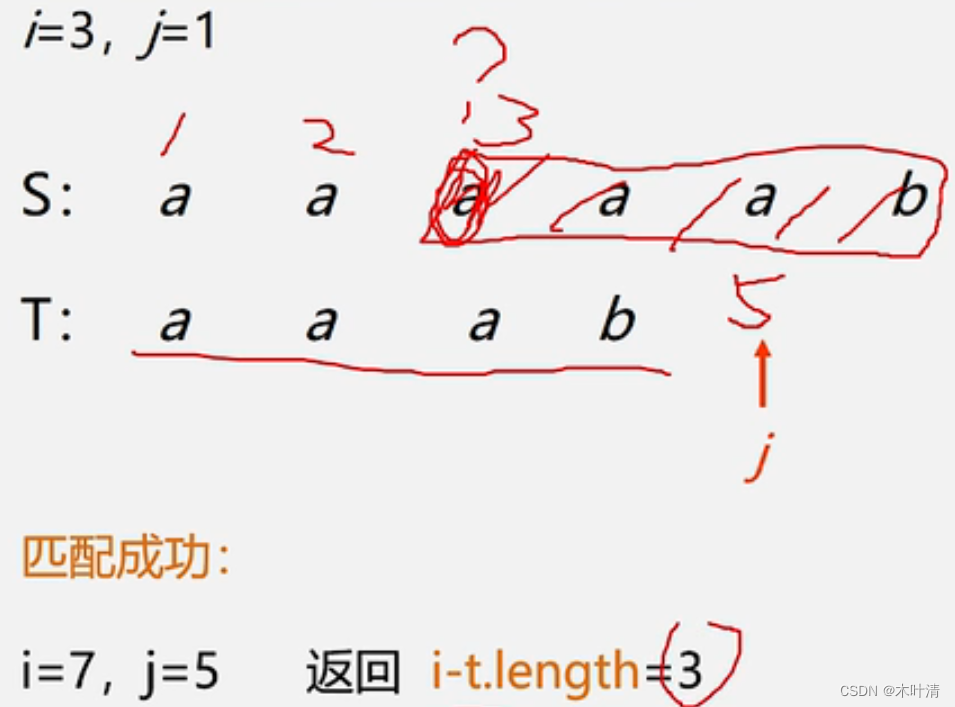


若主串长度为n,子串长度为m, BT算法的时间复杂度为O(n*m)