《acwing算法基础》简单算法

快速排序:

思路:

1. 给定一个无序的数组.

2. 选定一个基准值x(建议数组的中间数字),一个指针left,一个指针right,left指向第一个元素,right指向第二个元素.,保证left下标永远小于等于right下标的前提下,如果数组left下标的值小于基准值数字,则left++,直到找到arr[left]>=x,如果数组right下标的值大于基准值数字,则right–,直到找到arr[right]<=x,将这两个元素进行交换.循环进行,直到基准值左下标的值小于等于x,基准值右下标的值大于等于x.

3. 递归左区间与右区间.

时间复杂度:

O(nlogn)

代码:

import java.util.Scanner;
public class Main{public static int[] arr = new int[1000010];public static void quick_sort(int[] arr,int l,int r) {if(l>=r){return;}int i = l-1;int j = r+1;             int q = arr[l+r>>1];        //基准值(用于比较)while(i<j){do{i++;}while(arr[i]<q);do{j--;}while(arr[j]>q);if(i<j){int tmp = arr[i];arr[i] = arr[j];arr[j] = tmp;}}quick_sort(arr,l,j);quick_sort(arr,j+1,r);}public static void main(String[] args){Scanner sc = new Scanner(System.in);int n = sc.nextInt();for(int i = 0;i < n;i++){arr[i] = sc.nextInt();}quick_sort(arr,0,n-1);for(int i = 0;i < n;i++){System.out.print(arr[i]+" ");}}

在代码中,基准值选择l或者r,都会容易出现边界问题.所以建议以中间的元素为基准值,确保不会有边界问题的出现

快排边界问题:

• 第一种情况:

• 

• 第二种情况:

• 

练习题:

给定一个长度为 n 的整数数列，以及一个整数 k，请用快速选择算法求出数列从小到大排序后的第 k 个数。

归并排序:

思路:

1. 确定分界点:一般以中间为界限

2. 进行递归排序

3. 归并

时间复杂度:

n(logn)

是一个稳定的排序算法

代码:

import java.util.Scanner;
public class Main{public static int[] arr = new int[1000010];public static int[] tmp = new int[1000010];public static void marge_sort(int[] q,int l,int r){if(l>=r){return;}int mid = l+r>>1;marge_sort(q,l,mid);marge_sort(q,mid+1,r);int k = 0;int i = l;int j = mid+1;while(i<=mid&&j<=r){if(q[i]<q[j]){tmp[k] = q[i];k++;i++;}else{tmp[k] = q[j];k++;j++;}}while(i<=mid){tmp[k] = q[i];i++;k++;}while(j<=r){tmp[k] = q[j];k++;j++;}for(i = l,j=0;i<=r;i++,j++){arr[i] = tmp[j];}}public static void main(String args[]){Scanner sc = new Scanner(System.in);int n = sc.nextInt();for(int i =0;i<n;i++){arr[i] = sc.nextInt();}marge_sort(arr,0,n-1);for(int i = 0;i < n;i++){System.out.print(arr[i]+" ");}}
}

练习题:

给定一个长度为 n 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 i 个和第 j 个元素，如果满足 i<j 且 a[i]>a[j]，则其为一个逆序对；否则不是。

输入格式

第一行包含整数 n，表示数列的长度。

第二行包含 n 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

二分思想:

思路:

在我们之前对于二分的理解中,二分用于对有序数组的查询,达到时间复杂度为O(logn)的算法.

但是二分其实不仅仅只适用于有序数组,在满足一定条件的数组或者字符串一样可以成立.

时间复杂度:

O(logn)

代码:

Boolean check(int x) {/* ... */} // 检查x是否满足某种性质// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
int bsearch_1(int l, int r)
{while (l < r){int mid = l + r >> 1;// check()判断mid是否满足性质//当题目中有多个答案时,这个模板可以求的序列满足条件的第一个答案.if (check(mid)) r = mid;    else l = mid + 1;}return l;
}
// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
int bsearch_2(int l, int r)
{while (l < r){int mid = l + r + 1 >> 1;//当题目中有多个答案时,这个模板可以求的序列满足条件的最后一个答案.if (check(mid)) l = mid;else r = mid - 1;}return l;
}
//浮点数二分:
bool check(double x) {/* ... */} // 检查x是否满足某种性质double bsearch_3(double l, double r)
{const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求while (r - l > eps){double mid = (l + r) / 2;if (check(mid)) r = mid;else l = mid;}return l;
}

练习题:

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

import java.util.*;
public class Main{public static void main(String avgs[]){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();int[] array = new int[n];for(int i = 0;i < n;i++){array[i] = scan.nextInt();}while(m!=0){int x = scan.nextInt();int l = 0;int r = n-1;while(l<r){int mid = (l+r)/2;if(array[mid] >= x){r = mid;}else{l = mid+1;}}if(array[l] != x){System.out.println("-1 -1");m--;}else{System.out.printf(l+" ");l = 0;r = n-1;while(l<r){int mid = (l+r+1)/2;if(array[mid] <= x){l = mid;}else{r = mid-1;}}System.out.println(l);m--;}}}
}

对于第一个模版,可以得到序列中满足x的第一个值,对于第二个模版,可以得到序列中满足x的最后一个值.

一维前缀合与二维前缀和:

通过前缀合可以得到数组0-x的值.

一维:

S[i] = a[1] + a[2] + ... a[i]
a[l] + ... + a[r] = S[r] - S[l - 1]

二维:

//第i行j列格子左上部分所有元素的和
//以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵的和为：S[i, j] = S[x2, y2] - S[x1 - 1, y2] - S[x2, y1 - 1] + S[x1 - 1, y1 - 1]

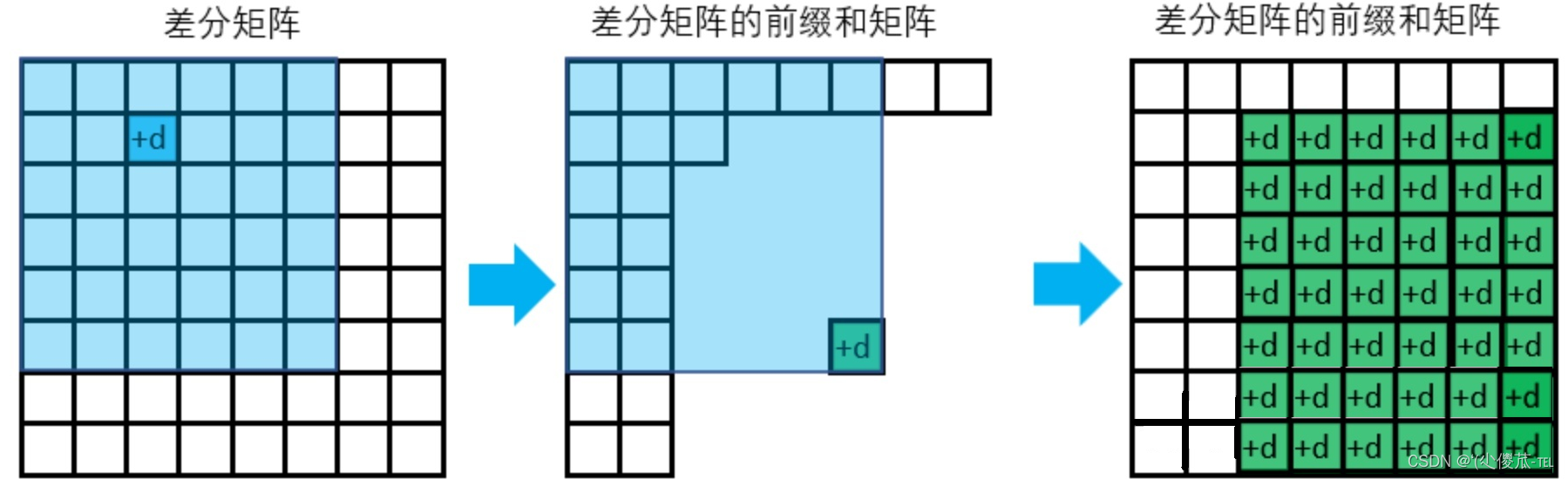
差分:

在构造差分数组时,一样使用insert直接插入就能得到差分数组.

通过差分可以以O(1)的复杂度为数组[l-r]的数字都加上每一个数.

一维:

给区间[l, r]中的每个数加上c：
B[l] += c, B[r + 1] -= c

二维:

给以(x1, y1)为左上角，(x2, y2)为右下角的子矩阵中的所有元素加上c：
S[x1, y1] += c, S[x2 + 1, y1] -= c, S[x1, y2 + 1] -= c, S[x2 + 1, y2 + 1] += c

二维矩阵练习题:

输入一个n行m列的整数矩阵，再输入q个操作，每个操作包含五个整数x1, y1, x2, y2, c，其中(x1, y1)和(x2, y2)表示一个子矩阵的左上角坐标和右下角坐标。

每个操作都要将选中的子矩阵中的每个元素的值加上c。

请你将进行完所有操作后的矩阵输出。

BufferReader输入为什么比Scanner快?:

• BufferedReader相对于Scanner来说要快一点，因为Scanner对输入数据进行正则解析，而BufferedReader只是简单地读取字符序列

详解参考大佬的解释: (卡了Scanner的输入导致超时,不看大佬的真的debug不出来.)

AcWing 798. 【Java】差分矩阵 - AcWing

import java.io.*;public class Main {private static int N = 1010;private static int M = 1010;private static int[][] a = new int[N][M];private static int[][] b = new int[N][M];public static void main(String[] args) throws Exception{BufferedReader reader = new BufferedReader(new InputStreamReader(System.in));BufferedWriter writer = new BufferedWriter(new OutputStreamWriter(System.out));String[] str = reader.readLine().split(" ");int n = Integer.parseInt(str[0]);int m = Integer.parseInt(str[1]);int q = Integer.parseInt(str[2]);for(int i = 1; i < n + 1; i++){str = reader.readLine().split(" ");for(int j = 1; j < m + 1; j++){//这里str下标是j-1a[i][j] = Integer.parseInt(str[j - 1]);//构造差分矩阵binsert(b,i,j,i,j,a[i][j]);}}while(q-- > 0){str = reader.readLine().split(" ");int x1 = Integer.parseInt(str[0]);int y1 = Integer.parseInt(str[1]);int x2 = Integer.parseInt(str[2]);int y2 = Integer.parseInt(str[3]);int c = Integer.parseInt(str[4]);insert(b,x1,y1,x2,y2,c);}for(int i = 1; i < n + 1; i++){for(int j = 1; j < m + 1; j++){//求矩阵前缀和//这里写+=后面就不用+b[i][j]了，否则是双倍b[i][j] = b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1] + b[i][j];writer.write(b[i][j] + " ");}writer.write("\n");}writer.flush();writer.close();reader.close();}public static void insert(int[][] b, int x1, int y1, int x2, int y2, int c){b[x1][y1] += c;b[x1][y2 + 1] -= c;b[x2 + 1][y1] -= c;b[x2 + 1][y2 + 1] += c;}
}

双指针算法:

模板:

for (int i = 0, j = 0; i < n; i ++ )
{while (j < i && check(i, j)) j ++ ;// 具体问题的逻辑
}

练习题:

答案:

import java.util.*;
public class Main{public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int[] arr = new int[n];int[] s = new int[100010];for(int i = 0;i<n;i++){arr[i]=scan.nextInt();}int m = 0;for(int i = 0,j = 0;i < n;i++){s[arr[i]]++;while(j<i&&s[arr[i]]>1){s[arr[j]]--;j++;}m = Math.max(m,i-j+1);}System.out.println(m);}
}

二进制算法:

求n的第k位数字: n >> k & 1
返回n的最后一位1：lowbit(n) = n & -n

离散化:

主要用于数据值大,但数据量稀疏(少)

模板:

public static int Unique(List<Integer> list){int j = 0;for(int i = 0;i < list.size();i++){if(i==0||list.get(i)!=list.get(i-1)){list.set(j,list.get(i));j++;}}return j;}
//进行离散化Collections.sort(alls); //对alls 的所有数都进行排序int unique = Unique(alls); //对alls进行去重并记录下最后的下标.(其实就是重复的数字都放在了unique下标之后)alls = alls.subList(0,unique);//拿到unqiue之前所有的数
public static int find(int x,List<Integer> list){int l = 0;int r = list.size()-1;while(l<r){int mid = l+r>>1;if(list.get(mid)>=x){r = mid;}else{l = mid+1;}}return l+1;  //看题目要求 
}

练习:

import java.util.*;
class pair{public int first = 0;public int second = 0;pair(int a,int b){first = a;second = b;}}
public class Main{public static int find(int x,List<Integer> list){int l = 0;int r = list.size()-1;while(l<r){int mid = l+r>>1;if(list.get(mid) >= x){r = mid;}else{l = mid + 1;}}return l + 1;}public static int Unique(List<Integer> list){int j = 0;for(int i = 0;i < list.size();i++){//千万别写成while了.if(i==0||list.get(i)!=list.get(i-1)){list.set(j,list.get(i));j++;}}return j;}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();int m = scan.nextInt();int T = 300010;//存储 x,l,r  n+2m <= 300000int[] a = new int[T];//作为存储数据的数组int[] s = new int[T];//作为前缀和的数组List<Integer> alls = new ArrayList<>();//存储所有操作数 x,l,r (这份数据需要进行离散化的,将每个数据都离散化为顺序表的坐标)List<pair> add = new ArrayList<>();//存储 x和cList<pair> option = new ArrayList<>();//存储操作数 l,rfor(int i = 0; i < n;i++){int x = scan.nextInt();int c = scan.nextInt();add.add(new pair(x,c));alls.add(x);}for(int i = 0;i < m;i++){int l = scan.nextInt();int r = scan.nextInt();option.add(new pair(l,r));alls.add(l);alls.add(r);}//进行离散化Collections.sort(alls); //对alls 的所有数都进行排序int unique = Unique(alls); //对alls进行去重并记录下最后的下标.(其实就是重复的数字都放在了unique下标之后)alls = alls.subList(0,unique);//拿到unqiue之前所有的数for(pair p:add){int index = find(p.first,alls);a[index] += p.second; }//构造前缀和for(int i = 1; i <= alls.size();i++){s[i] = s[i-1]+a[i];}//m次询问for(pair p:option){int l = find(p.first,alls);int r = find(p.second,alls);System.out.println(s[r]-s[l-1]);}}
}

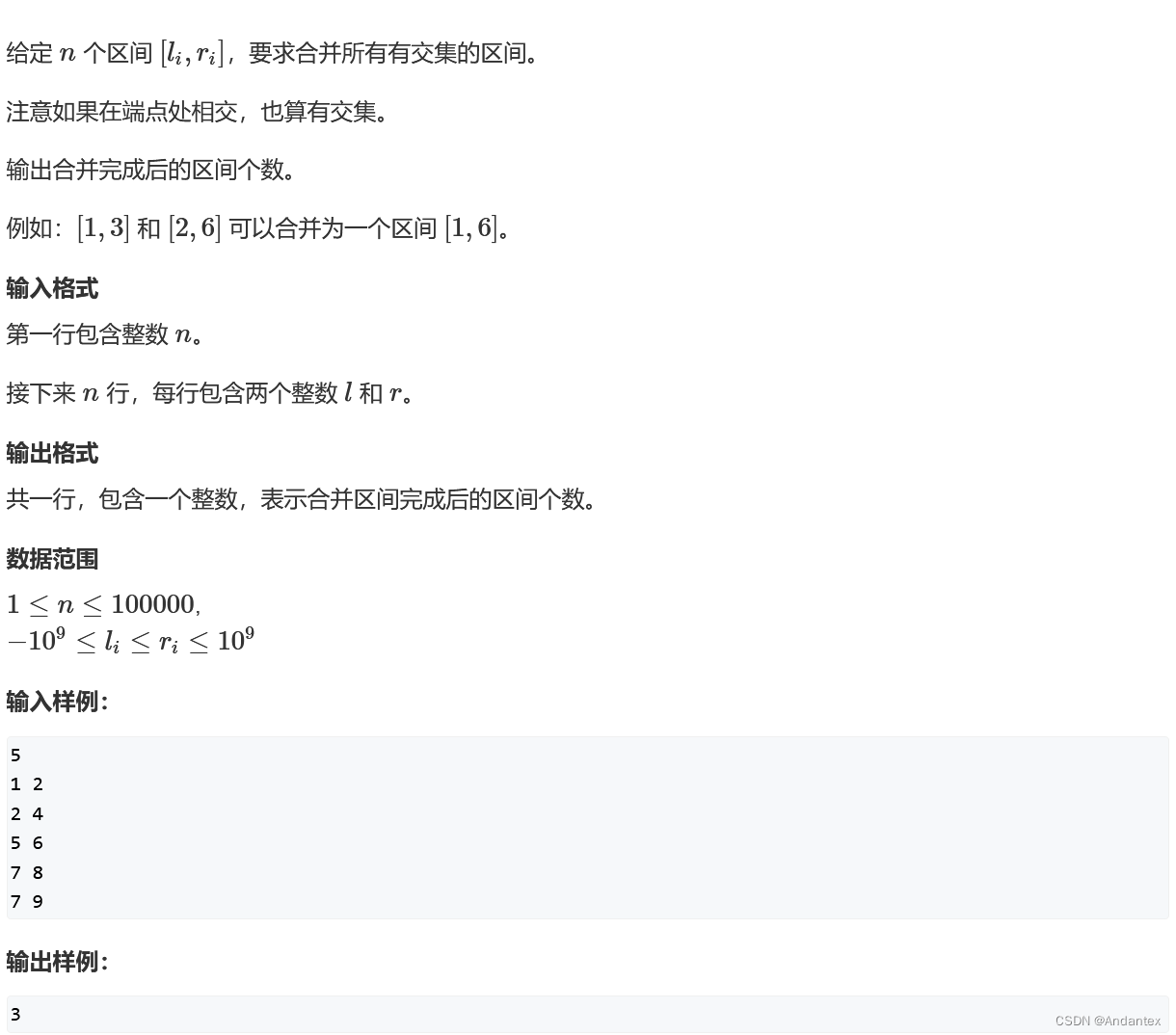
区间合并:

模板:

 public static List<pair> mearge(List<pair> list){//对 list集合进行自定义排序.Collections.sort(list,new Comparator<pair>(){public int compare(pair p1,pair p2){return p1.l - p2.l;}  });List<pair> ret = new ArrayList<>();int st = (int)-2e9;int ed = (int)-2e9;for(int i = 0;i < list.size();i++){if(ed < list.get(i).l){if(st != -2e9){ret.add(new pair(st,ed));}st = list.get(i).l;ed = list.get(i).r;}else{ed = Math.max(ed,list.get(i).r);}}if(st!=-2e9){ret.add(new pair(st,ed));}return ret;}

练习题:

import java.util.*;
class pair{public int first = 0;public int second = 0;public pair(int a ,int b){first = a;second = b;}
}
public class Main{public static List<pair> result(List<pair> list){Collections.sort(list,new Comparator<pair>(){public int compare(pair p1,pair p2){return p1.first - p2.first;}});int st = (int)-2e9;int ed = (int)-2e9;List<pair> ret = new ArrayList<>();for(int i = 0;i < list.size();i++){if(ed<list.get(i).first){//第一次不能加入if(st!=-2e9){ret.add(new pair(st,ed));}st = list.get(i).first;ed = list.get(i).second;}else{ed = Math.max(ed,list.get(i).second);}}if(st!=-2e9){ret.add(new pair(st,ed));}return ret;}public static void main(String[] args){Scanner scan = new Scanner(System.in);int n = scan.nextInt();List<pair> list = new ArrayList<>();for(int i = 0;i < n;i++){int l = scan.nextInt();int r = scan.nextInt();list.add(new pair(l,r));}list = result(list);System.out.println(list.size());}
}

技巧:

输出有效位浮点数:

        System.out.println(String.format("%.6f", l));

判断重复:

使用数组.

799. 最长连续不重复子序列 - AcWing题库

使用hashmap

对List类进行排序的:

//注意 ,里面没有实现list的泛型类排序,需要自己引入comparator.(比较器)
Collections.sort(list);