免疫算法（二进制）算例（源码实现）

article/2025/9/24 13:07:45

之前我们讲解了免疫算法以及离散的免疫算法。见链接：
万字长文了解免疫算法原理及求解复杂约束问题（源码实现）
离散免疫算法求解旅行商问题(源码实现)

今天讲下二进制的免疫算法。
我爱学习，爱玉酱。

算例

假设一个数PD=210，它可以看成下列中的数，某几个组合而成来的。
P_state=np.array([1700,2600,180,2200,1400,60,85,290,4100,3000,1590,200,1300,50,100,30,90])，即PD=sum（x_iP_state_i）其中的x_i表示状态，只能取0或1。
限制条件：【180,2200】,序号[2,3]不能共存；【60,85,300】,序号[5,6,7]不能共存；【50,100】序号[13,14]不能共存；【25,90】序号[15,16]不能共存。

算例实现

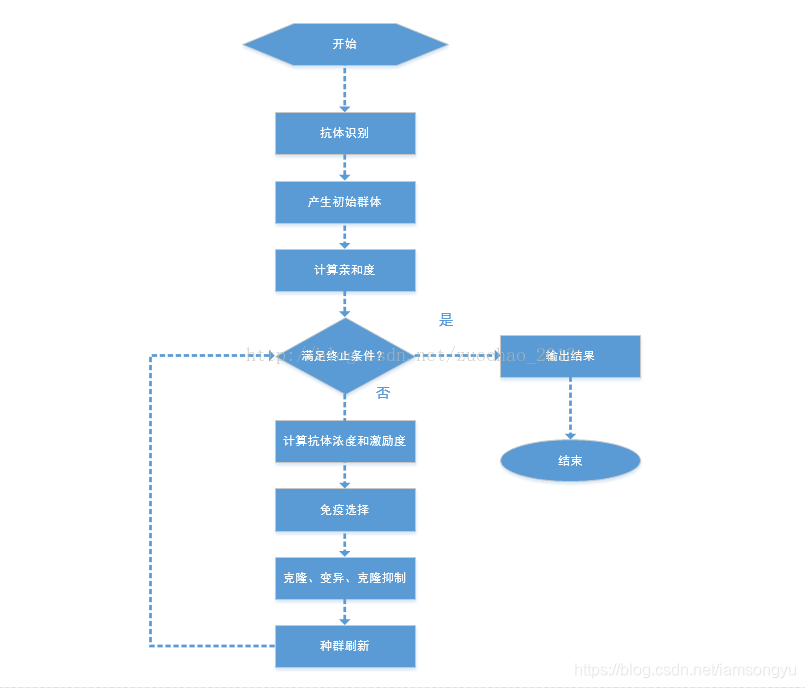
如果不懂算法原理，请看之前免疫算法博文。
由于二进制编码不可能出现重复，所以无需计算浓度。

python实现
python3.7

#!/usr/bin/env python3
# -*- coding: utf-8 -*-
# @Author: yudengwu(余登武）
# @Date  : 2021/5/19
#@email:1344732766@qq.com
import pandas as pd
import numpy as np
from tqdm import tqdm#进度条设置
import matplotlib.pyplot as plt
import matplotlib; matplotlib.use('TkAgg')
from pylab import *
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False#以一个负荷为例讲解优化算法P_state=np.array([1700,2600,180,2200,1400,60,85,290,4100,3000,1590,200,1300,50,100,30,90])#17个状态state_num=17 #状态数
#【180,2200】,序号[2,3]不能共存
#【60,85,300】,序号[5,6,7]不能共存
#【50,100】 序号[13,14]不能共存
#【25,90】序号[15,16]不能共存#总负荷
Pload=446.0 #这个值可以设置的########适应度函数
def calc_f(xi):""":param xi 为个体  即电器的工作状态，01二二进制，0表示当前状态关，1表示开:xi 为np.array(数据）:return  返回 np.abs(XiP_state-pload) P_state为电器"额定功率":"""xi=np.array(xi)xi=xi.reshape(state_num,)return np.abs(np.sum(xi*P_state)-Pload)###############免疫算法相关函数#############
#免疫操作函数：克隆、变异、变异抑制
def variation(Sortf):""":param Sortf : 排序后的种群:return: 经过克隆、变异、变异抑制后的群体af .af的规模为Sortf的一半"""Ncl = 5  # 克隆个数af = np.zeros((np.int(NP / 2), state_num))  # 存储变异后的个体for i in range(np.int(NP / 2)):  # 遍历前一半个体# 选激励度前NP/2个体进行免疫操作a = Sortf[i]  # 当前个体 .shape(state_num,)a = a.reshape(-1, state_num)  # （-1，维度state_num）Na = np.tile(a, (Ncl, 1))  # 对当前个体进行克隆 Na.shape=(Ncl, state_num)for j in range(Ncl):  # 遍历每一个克隆样本for k in range(state_num):#遍历个体的每一个元素#变异if np.random.random()<0.5:#Na[j,k]=1else:Na[j,k]=0# 【180,2200】,序号[2,3]不能共存while Na[j, 2] + Na[j, 3]  == 2 :Na[j, 2] = np.random.randint(0, 2, 1)Na[j, 3] = np.random.randint(0, 2, 1)# 【60,85,300】,序号[5,6,7]不能共存while Na[j, 5] + Na[j, 6] + Na[j, 7] == 2 or Na[j, 5] + Na[j, 6] + Na[j, 7] == 3:Na[j, 5] = np.random.randint(0, 2, 1)Na[j, 6] = np.random.randint(0, 2, 1)Na[j, 7] = np.random.randint(0, 2, 1)# 【50,100】 序号[13,14]不能共存while Na[j, 13] + Na[j, 14] == 2:Na[j, 13] = np.random.randint(0, 2, 1)Na[j, 14] = np.random.randint(0, 2, 1)# 【25,90】序号[15,16]不能共存while Na[j, 15] + Na[j, 16] == 2:Na[j, 15] = np.random.randint(0, 2, 1)Na[j, 16] = np.random.randint(0, 2, 1)# 保留克隆源个体Na[0, :] = Sortf[i]#####克隆抑制，保留亲和度最高的个体NaMSLL = np.zeros((Ncl, 1))  # 存储变异种群亲和度值for j in range(Ncl):  # 遍历每一个克隆样本NaMSLL[j] = calc_f(xi=Na[j])  # 亲和度=距离Index = np.argsort(NaMSLL, axis=0)  # 激励度按升序排序Index = Index[:, 0]NaSortf = Na[Index]  # 排序后的种群af[i] = NaSortf[0]  # 取最优return af#免疫操作：创建新生种群
def refresh():""":return: 创建一半新生群体 bf"""#########初始化群体bf = np.random.randint(0, 2, (np.int(NP/2), state_num))  # 在[0,2）之前随机取整数，取state_num(19)个 bf.shape=(50, 19)for j in range(np.int(NP / 2)):  # 遍历每一个个体# 【180,2200】,序号[2,3]不能共存while bf[j, 2] + bf[j, 3] == 2:bf[j, 2] = np.random.randint(0, 2, 1)bf[j, 3] = np.random.randint(0, 2, 1)# 【60,85,300】,序号[5,6,7]不能共存while bf[j, 5] + bf[j, 6] + bf[j, 7] == 2 or bf[j, 5] + bf[j, 6] + bf[j, 7] == 3:bf[j, 5] = np.random.randint(0, 2, 1)bf[j, 6] = np.random.randint(0, 2, 1)bf[j, 7] = np.random.randint(0, 2, 1)# 【50,100】 序号[13,14]不能共存while bf[j, 13] + bf[j, 14] == 2:bf[j, 13] = np.random.randint(0, 2, 1)bf[j, 14] = np.random.randint(0, 2, 1)# 【25,90】序号[15,16]不能共存while bf[j, 15] + bf[j, 16] == 2:bf[j, 15] = np.random.randint(0, 2, 1)bf[j, 16] = np.random.randint(0, 2, 1)return bf#############免疫算法开始############
NP=100                          #免疫个体数目
G=200                          #最大免疫代数#########初始化群体
f=np.random.randint(0,2,(NP,state_num)) #在[0,2）之前随机取整数，取state_num(19)个 f.shape=(100, 19)
for j in range(NP):while f[j, 2] + f[j, 3] == 2:f[j, 2] = np.random.randint(0, 2, 1)f[j, 3] = np.random.randint(0, 2, 1)# 【60,85,300】,序号[5,6,7]不能共存while f[j, 5] + f[j, 6] + f[j, 7] == 2 or f[j, 5] + f[j, 6] + f[j, 7] == 3:f[j, 5] = np.random.randint(0, 2, 1)f[j, 6] = np.random.randint(0, 2, 1)f[j, 7] = np.random.randint(0, 2, 1)# 【50,100】 序号[13,14]不能共存while f[j, 13] + f[j, 14] == 2:f[j, 13] = np.random.randint(0, 2, 1)f[j, 14] = np.random.randint(0, 2, 1)# 【25,90】序号[15,16]不能共存while f[j, 15] + f[j, 16] == 2:f[j, 15] = np.random.randint(0, 2, 1)f[j, 16] = np.random.randint(0, 2, 1)len=np.zeros((NP,1))                  #存储calc_f(X)结果for i in range(NP):#遍历每一个个体len[i]=calc_f(xi=f[i]) #计算初始群体每个个体的路程长度
###激励度按升序排序
Index=np.argsort(len,axis=0)
Index=Index[:,0]
Sortf=f[Index] # #排序后的初始群体 shape=(100, 18)##############免疫循环############
trace=[] #记录迭代激励度最优值
for gen in tqdm(range(G)):#遍历每一次迭代af = variation(Sortf)  # 选择一半个体 进行克隆、变异、变异抑制 shape=(100, 18)aflen=np.zeros((af.shape[0],1))                  #存储af群体路径长度 shape=(100, 1)for j in range(af.shape[0]):#遍历af中的每一个个体aflen[j] = calc_f(xi=af[j]) # 计算af群体每个个体的路程长度(亲和度）bf = refresh()  # 创建一半新生种群#bf.shape=(100, 18)bflen = np.zeros((bf.shape[0], 1))  # 存储bf群体路径长度 shape=(100, 1)for j in range(bf.shape[0]):  # 遍历bf中的每一个个体bflen[j] = calc_f(xi=bf[j])  # 计算bf群体每个个体的路程长度(亲和度）# ##########种群刷新：免疫种群与新生种群合并##f1 = np.concatenate((af, bf), axis=0)  # 合并的种群 f1.shape=(50, 18) f1为子代f1len = np.concatenate((aflen, bflen), axis=0)  # 合并种群激励度值 shape=(200, 1)Index = np.argsort(f1len, axis=0)Index = Index[:, 0]Sortf = f1[Index]  # shape(50, 18)trace.append(calc_f(xi=f1[0]))  # 记录最优个体的激励度值############输出优化结果
Bestf=Sortf[0,:]                #最优变量
print('最优变量',Bestf)
print('误差',trace[-1] )       #最优值
print('最优值',np.array(Bestf)*P_state)
plt.plot(trace)
plt.title('迭代曲线')
plt.xlabel('迭代次数')
plt.ylabel('abs(sum(xi*Pi)-Pload)')
plt.show()