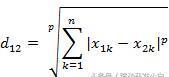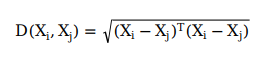免疫算法Python实现

1.流程

在这里插入图片描述

免疫算法与遗传算法其实非常相似，但其独特的地方在于，免疫算法用激励度而非亲和度来衡量结果的好坏，而激励度又与抗体密度有关，这就使得密度大的抗体激励度反而小，让免疫算法有全局搜索的能力，不容易陷入局部最优，接下来我就结合代码来讲解。

2.开发环境

【Anaconda + jupyter notebook python 3.7.9】

3.具体实例

现有一函数 $f(x,y) = 5sin(xy) + x^{2} + y^{2}$ ,定义域为 $x\in [-4,4],y\in [-4,4]$ ,函数图像

首先导入需要的包

numpy

pandas(这个好像全程没用到)

matplotlib(绘制三维图)

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

定义需要的参数

因为所求的函数为二元，故维度为2

choice的值表示所求的为最大还是最小值，如果求的是最大值，那么alpha就要为正，反之为负(后面会解释)

G = 100    #迭代次数
fun = '5 * sin(x * y) + x ** 2 + y ** 2'   #目标函数
choice = 'max'
dim = 2                    #维度
limit_x = [-4,4]           #x取值范围
limit_y = [-4,4]           #y取值范围
pop_size = 10              #种群规模
mutate_rate = 0.7          #变异概率
delta = 0.2                #相似度阈值
beta = 1                   #激励度系数
colone_num = 10            #克隆份数
if choice == 'max':alpha = 2              #激励度系数,求最大值为正,最小值为负
else:alpha = -2

首先定义一些函数

传入函数表达式和自变量的值，返回函数值

def f(fun,x,y):       #函数表达式return eval(fun)

初始化种群函数

生成一个 dim x pop_size 的矩阵，在这里即为 2 x 10，每一列代表一个个体，第一行表示x，第二行表示y。

传入尺寸和取值范围，随机生成范围内的x，y值，公式： x = rand * (上限 - 下限) + 下限，rand为0~1之间的随机数

#初始化种群
def init_pop(dim,pop_size,*limit):pop = np.random.rand(dim,pop_size)for i in range(dim):pop[i,:] *= (limit[i][1] - limit[i][0])pop[i,:] += limit[i][0]return pop

计算浓度

生成的density为 1x10 维的矩阵，表示每一个个体的浓度，

首先计算每一个个体与其他个体的相似度，计算公式即为两点间距离公式

$\sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}$

对于每一个个体，计算完相似度后可以得到一个 1x10 的矩阵，矩阵中的元素如果小于给定的阈值，则认为两个个体相似，并赋值为1，否则赋值为0。经过上述相似度判断后所得到的 1x10 矩阵中的元素只有1和0.然后将所有相似度相加，并除以总个数便得到该个体的浓度。

#计算浓度
def calc_density(pop,delta):density = np.zeros([pop.shape[1],])for i in range(pop.shape[1]):density[i] = np.sum(len(np.ones([pop.shape[1],])[np.sqrt(np.sum((pop - pop[:,i].reshape([2,1])) ** 2,axis = 0)) < delta]))return density / pop.shape[1]

计算激励度

传入的simulation参数为亲和度(其实就是每个个体的x，y带入得到的函数值)，若要求的是最大值，则alpha为正(因为值越大得到的激励度越大)，否则alpha为负。减去浓度是为了全局搜索，浓度大的则激励度小，这样其他浓度小的个体也有机会进行接下来的克隆变异操作。

#计算激励度
def calc_simulation(simulation,density):return (alpha * simulation - beta * density)

变异操作

每个个体的x，y都有一定概率变异，变异即加上一个随机数，如果超过了定义域，则重新生成，gen代表遗传的代数，代数越大，则每次变异的范围应该越小(因为繁殖代数越多，所得到的个体就越接近最优解，此时应减小变异的范围使其收敛)

#变异，随着代数增加变异范围逐渐减小
def mutate(x,gen,mutata_rate,dim,*limit):for i in range(dim):if np.random.rand() <= mutata_rate:x[i] += (np.random.rand() - 0.5) * (limit[i][1] - limit[i][0]) / (gen + 1)    #加上随机数产生变异if (x[i] > limit[i][1]) or (x[i] < limit[i][0]):      #边界检测x[i] = np.random.rand() * (limit[i][1] - limit[i][0]) + limit[i][0]

到此为止，函数已经定义完，接下来就要开始免疫迭代了

免疫循环

首先生成初始种群pop，init_simulation表示亲和度，然后算出浓度(密度)density，根据亲和度和密度计算出激励度

pop = init_pop(dim,pop_size,limit_x,limit_y)
init_simulation = f(fun,pop[0,:],pop[1,:])
density = calc_density(pop,delta)
simulation = calc_simulation(init_simulation,density)

接下来进行排序,按照激励度降序排列。这边的new_pop为一份拷贝,在后面需要用到,而且应该进行浅拷贝防止影响原来的pop

#进行激励度排序
index = np.argsort(-simulation)
pop = pop[:,index]
new_pop = pop.copy()    #浅拷贝
simulation = simulation[index]

取激励度前50%的个体进行免疫操作，首先生成两个矩阵用于存放筛选出来的个体和其激励度。每一个个体都克隆10份，然后进行变异操作。变异完后保留克隆源个体。接下来对变异后的10个个体进行激励度计算并排序，筛选出最优的那个并放入先前生成的矩阵中。

筛选出来的最优为5个，再随机生成5个个体，将两组合并即组成一个新的种群。之后重复上述操作即可

#免疫循环
for gen in range(G):best_a = np.zeros([dim,int(pop_size / 2)])   #用于保留每次克隆后亲和度最高的个体best_a_simulation = np.zeros([int(pop_size / 2),]) #保存激励度#选出激励度前50%的个体进行免疫for i in range(int(pop_size / 2)):a = new_pop[:,i].reshape([2,1])b = np.tile(a,(1,colone_num))   #克隆10份for j in range(colone_num):mutate(a,gen,mutate_rate,dim,limit_x,limit_y)b[:,0] = pop[:,i]       #保留克隆源个体#保留亲和度最高的个体b_simulation = f(fun,b[0,:],b[1,:])index = np.argsort(-b_simulation)best_a_simulation = b_simulation[index][0]    #最佳个体亲和度best_a[:,i] = b[:,index][:,0]                 #最佳个体#计算免疫种群的激励度a_density = calc_density(best_a,delta)best_a_simulation = calc_simulation(best_a_simulation,a_density)#种群刷新new_a = init_pop(2,int(pop_size / 2),limit_x,limit_y)#新生种群激励度new_a_simulation = f(fun,new_a[0,:],new_a[1,:])new_a_density = calc_density(new_a,delta)new_a_simulation = calc_simulation(new_a_simulation,new_a_density)#免疫种群与新生种群合并pop = np.hstack([best_a,new_a])simulation = np.hstack([best_a_simulation,new_a_simulation])index = np.argsort(-simulation)pop = pop[:,index]simulation = simulation[index]new_pop = pop.copy()

最后进行绘图

# 新建一个画布
figure = plt.figure(figsize = (10,8),dpi = 80)
# 新建一个3d绘图对象
ax = Axes3D(figure)
# 定义x,y 轴名称
plt.xlabel("x")
plt.ylabel("y")
for i in range(int(pop_size / 2)):ax.scatter(pop[0,i],pop[1,i],f(fun,pop[0,i],pop[1,i]),color = 'red')print('最优解:','x = ',pop[0,i],'y = ',pop[1,i],end = '\n')print('结果:','z = ',f(fun,pop[0,i],pop[1,i]))
x = np.arange(limit_x[0],limit_x[1],(limit_x[1] - limit_x[0]) / 50)
y = np.arange(limit_y[0],limit_y[1],(limit_y[1] - limit_y[0]) / 50)
x,y = np.meshgrid(x,y)
z = f(fun,x,y)
ax.plot_surface(x,y,z, rstride=1, cstride=1, color = 'green',alpha = 0.5)
plt.show()

结果是这样

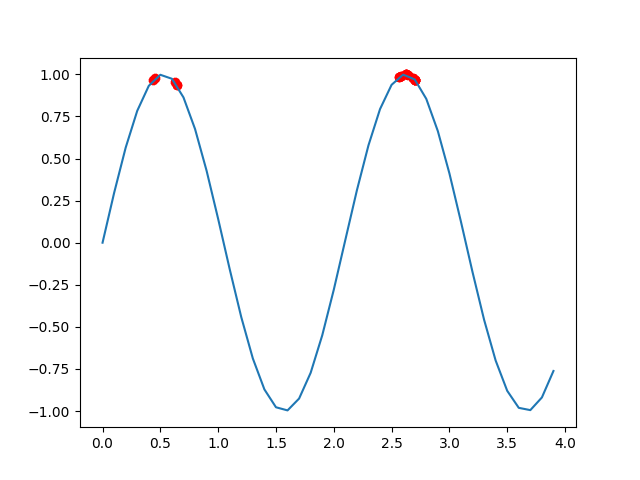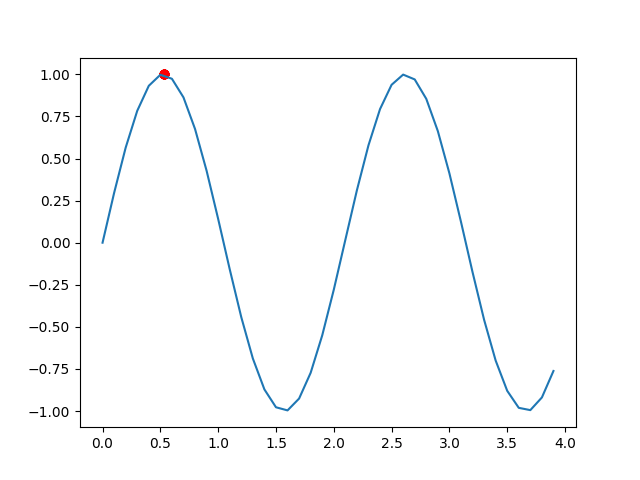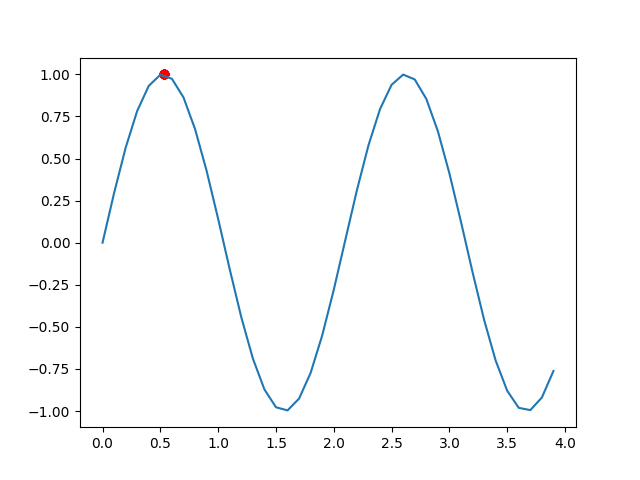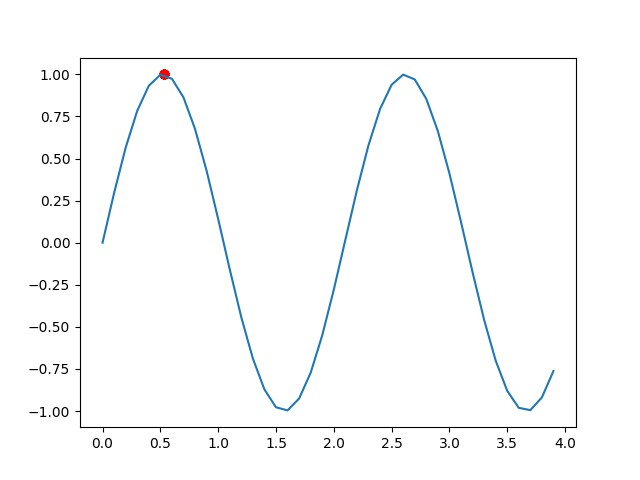
可以看到免疫算法并不局限于一个最值

这是最小值的情况

最后附上完整代码

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
from mpl_toolkits.mplot3d import Axes3DG = 100    #迭代次数
fun = '5 * sin(x * y) + x ** 2 + y ** 2'   #目标函数
choice = 'max'
dim = 2                    #维度
limit_x = [-4,4]           #x取值范围
limit_y = [-4,4]           #y取值范围
pop_size = 10              #种群规模
mutate_rate = 0.7          #变异概率
delta = 0.2                #相似度阈值
beta = 1                   #激励度系数
colone_num = 10            #克隆份数
if choice == 'max':alpha = 2              #激励度系数,求最大值为正,最小值为负
else:alpha = -2def f(fun,x,y):return eval(fun)#初始化种群
def init_pop(dim,pop_size,*limit):pop = np.random.rand(dim,pop_size)for i in range(dim):pop[i,:] *= (limit[i][1] - limit[i][0])pop[i,:] += limit[i][0]return pop#计算浓度
def calc_density(pop,delta):density = np.zeros([pop.shape[1],])for i in range(pop.shape[1]):density[i] = np.sum(len(np.ones([pop.shape[1],])[np.sqrt(np.sum((pop - pop[:,i].reshape([2,1])) ** 2,axis = 0)) < delta]))return density / pop.shape[1]#计算激励度
def calc_simulation(simulation,density):return (alpha * simulation - beta * density)#变异，随着代数增加变异范围逐渐减小
def mutate(x,gen,mutata_rate,dim,*limit):for i in range(dim):if np.random.rand() <= mutata_rate:x[i] += (np.random.rand() - 0.5) * (limit[i][1] - limit[i][0]) / (gen + 1)    #加上随机数产生变异if (x[i] > limit[i][1]) or (x[i] < limit[i][0]):      #边界检测x[i] = np.random.rand() * (limit[i][1] - limit[i][0]) + limit[i][0]pop = init_pop(dim,pop_size,limit_x,limit_y)
init_simulation = f(fun,pop[0,:],pop[1,:])
density = calc_density(pop,delta)
simulation = calc_simulation(init_simulation,density)
# print(pop)
# print(init_simulation)
# print(calc_density(pop,delta))
#进行激励度排序
index = np.argsort(-simulation)
pop = pop[:,index]
new_pop = pop.copy()    #浅拷贝
simulation = simulation[index]#免疫循环
for gen in range(G):best_a = np.zeros([dim,int(pop_size / 2)])   #用于保留每次克隆后亲和度最高的个体best_a_simulation = np.zeros([int(pop_size / 2),]) #保存激励度#选出激励度前50%的个体进行免疫for i in range(int(pop_size / 2)):a = new_pop[:,i].reshape([2,1])b = np.tile(a,(1,colone_num))   #克隆10份for j in range(colone_num):mutate(a,gen,mutate_rate,dim,limit_x,limit_y)b[:,0] = pop[:,i]       #保留克隆源个体#保留亲和度最高的个体b_simulation = f(fun,b[0,:],b[1,:])index = np.argsort(-b_simulation)best_a_simulation = b_simulation[index][0]    #最佳个体亲和度best_a[:,i] = b[:,index][:,0]                 #最佳个体#计算免疫种群的激励度a_density = calc_density(best_a,delta)best_a_simulation = calc_simulation(best_a_simulation,a_density)#种群刷新new_a = init_pop(2,int(pop_size / 2),limit_x,limit_y)#新生种群激励度new_a_simulation = f(fun,new_a[0,:],new_a[1,:])new_a_density = calc_density(new_a,delta)new_a_simulation = calc_simulation(new_a_simulation,new_a_density)#免疫种群与新生种群合并pop = np.hstack([best_a,new_a])simulation = np.hstack([best_a_simulation,new_a_simulation])index = np.argsort(-simulation)pop = pop[:,index]simulation = simulation[index]new_pop = pop.copy()# 新建一个画布
figure = plt.figure(figsize = (10,8),dpi = 80)
# 新建一个3d绘图对象
ax = Axes3D(figure)
# 定义x,y 轴名称
plt.xlabel("x")
plt.ylabel("y")
for i in range(int(pop_size / 2)):ax.scatter(pop[0,i],pop[1,i],f(fun,pop[0,i],pop[1,i]),color = 'red')print('最优解:','x = ',pop[0,i],'y = ',pop[1,i],end = '\n')print('结果:','z = ',f(fun,pop[0,i],pop[1,i]))
x = np.arange(limit_x[0],limit_x[1],(limit_x[1] - limit_x[0]) / 50)
y = np.arange(limit_y[0],limit_y[1],(limit_y[1] - limit_y[0]) / 50)
x,y = np.meshgrid(x,y)
z = f(fun,x,y)
ax.plot_surface(x,y,z, rstride=1, cstride=1, color = 'green',alpha = 0.5)
plt.show()

讲的可能不是特别清楚，也有可能有些地方理解不大对，有不懂的可以在评论区提问