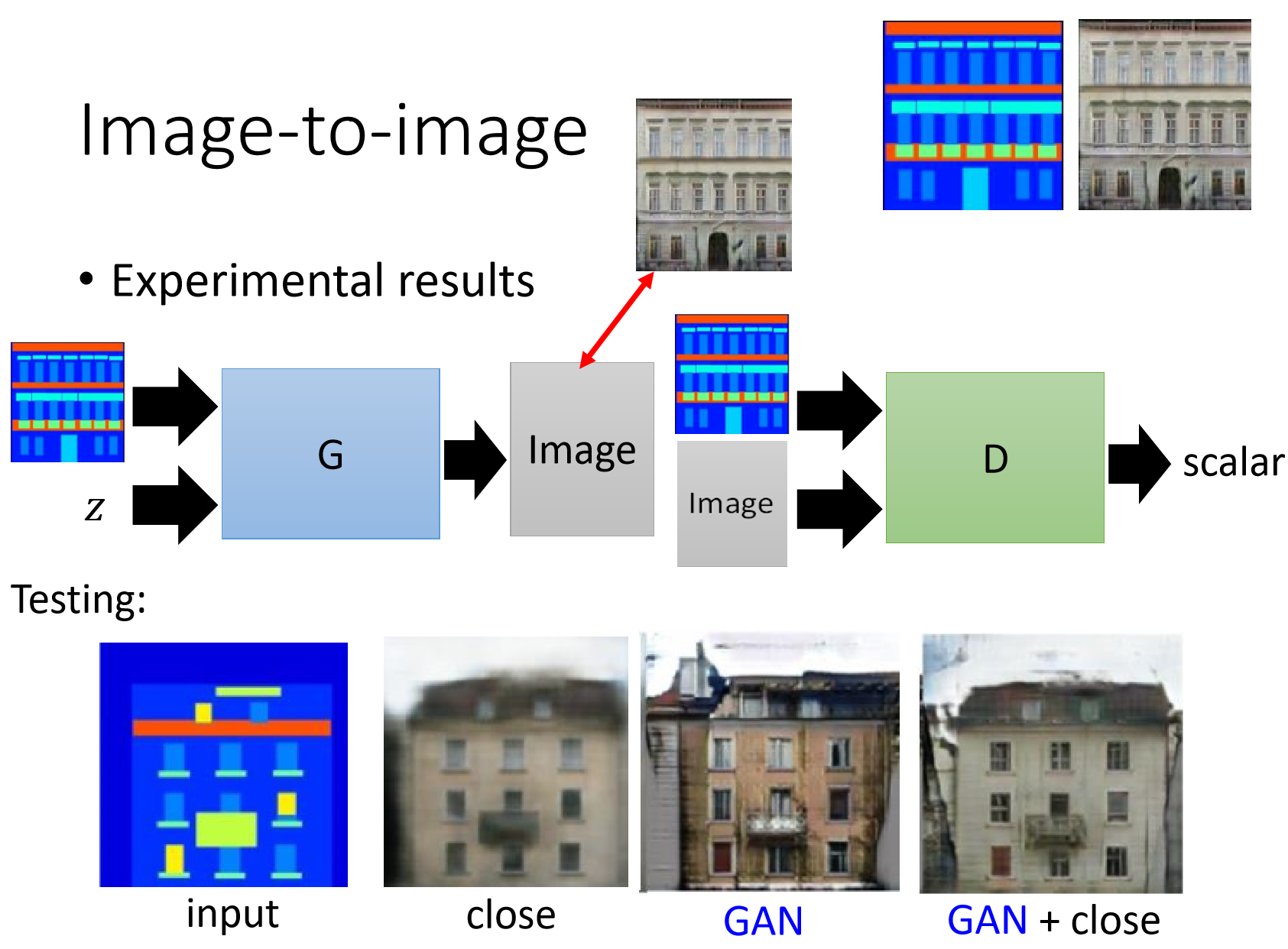
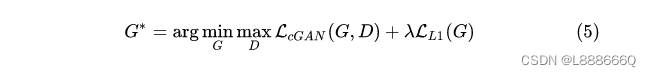DCGAN TUTORIAL

Introduction

本教程将通过一个示例对DCGAN进行介绍。在向其展示许多真实名人的照片之后，我们将训练一个生成对抗网络（GAN）来产生新名人。此处的大多数代码来自pytorch / examples中的dcgan实现，并且本文档将对该实现进行详尽的解释，并阐明此模型的工作方式和原因。但是请放心，不需要GAN的先验知识，但是可能需要新手花一些时间来推理引擎盖下的实际情况。同样，为了节省时间，拥有一两个GPU也将有所帮助。让我们从头开始。

生成对抗网络Generative Adversarial Networks

什么是GAN？What is a GAN?

GAN是用于教授DL模型以捕获训练数据分布的框架，因此我们可以从同一分布中生成新数据。GAN是Ian Goodfellow在2014年发明的，最早在Generative Adversarial Nets一书中进行了描述。它们由两个不同的模型组成：生成器和 鉴别器。生成器的工作是生成看起来像训练图像的“伪”图像。鉴别器的工作是查看图像并从生成器输出它是真实的训练图像还是伪图像。在训练过程中，生成器不断尝试通过生成越来越好的伪造品而使鉴别器的性能超过智者，而鉴别器正在努力成为更好的侦探并正确地对真实和伪造图像进行分类。博弈的平衡点是当生成器生成的伪造品看起来好像直接来自训练数据时，而鉴别器则总是猜测生成器输出是真实的或伪造品的50％置信度。

现在，让我们从鉴别符开始定义一些在整个教程中使用的符号。让x

x 是代表图像的数据。 D(x)

D(x) 是鉴别器网络，输出的（标量）概率为 x

x来自训练数据，而不是生成器。在这里，由于我们正在处理图像，因此输入 D(x)

D(x)是CHW大小为3x64x64的图像。凭直觉D(x)

D(x) 何时应为高 x

x 来自训练数据，低时 x

x 来自生成器。 D(x)

D(x) 也可以被认为是传统的二进制分类器。

对于生成器的符号，让 z

z 是从标准正态分布采样的潜在空间向量。 G(z)

G(z) 表示映射潜在向量的生成器函数 z

z到数据空间。的目标G

G 是为了估计训练数据来自（p

data

pdata），以便可以从该估计的分布中生成假样本（p

pg）。

所以， D(G(z))

D(G(z)) 是生成器输出的概率（标量） G

G是真实的图像。如Goodfellow的论文所述， D

D 和 G

G 玩一个minimax游戏，其中 D

D 尝试最大化其正确分类真假的可能性（logD(x)

logD(x)），以及 G

G 试图最小化以下可能性 D

D 会预测其输出是假的（log(1−D(G(x)))

log(1−D(G(x)))）。从本文来看，GAN损失函数为

min

max

V(D,G)=E

x∼p

data

(x)

[logD(x)]+E

z∼p

(z)

[log(1−D(G(z)))]

minGmaxDV(D,G)=Ex∼pdata(x)[logD(x)]+Ez∼pz(z)[log(1−D(G(z)))]

从理论上讲，此minimax游戏的解决方案是 p

data

pg=pdata，鉴别者会随机猜测输入是真实的还是假的。但是，GAN的收敛理论仍在积极研究中，实际上，模型并不总是能达到此目的。

什么是DCGAN？What is a DCGAN?

DCGAN是上述GAN的直接扩展，不同之处在于DCGAN分别在鉴别器和生成器中分别使用卷积和卷积转置层。它最早由Radford等人描述。等在纸张无监督表示学习凭借深厚的卷积剖成对抗性网络。鉴别器由跨步卷积层，批范数层和 LeakyReLU 激活组成。输入是3x64x64的输入图像，输出是输入来自真实数据分布的标量概率。生成器由卷积转置层，批处理规范层和 ReLU组成激活。输入是一个潜在向量，z

z，它是从标准正态分布中提取的，输出是3x64x64 RGB图像。跨步的转置图层允许将潜矢量转换为与图像具有相同形状的体积。在本文中，作者还提供了有关如何设置优化器，如何计算损失函数以及如何初始化模型权重的一些技巧，所有这些将在接下来的部分中进行解释。

from __future__ import print_function
#%matplotlib inline
import argparse
import os
import random
import torch
import torch.nn as nn
import torch.nn.parallel
import torch.backends.cudnn as cudnn
import torch.optim as optim
import torch.utils.data
import torchvision.datasets as dset
import torchvision.transforms as transforms
import torchvision.utils as vutils
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
from IPython.display import HTML

# Set random seed for reproducibility
manualSeed = 999
#manualSeed = random.randint(1, 10000) # use if you want new results
print("Random Seed: ", manualSeed)
random.seed(manualSeed)
torch.manual_seed(manualSeed)

输出：

Random Seed:  999

Inputs

让我们为运行定义一些输入：

dataroot-数据集文件夹根目录的路径。我们将在下一节中进一步讨论数据集
工人 -工作线程用于与的DataLoader加载数据的数
batch_size-训练中使用的批次大小。DCGAN纸使用的批处理大小为128
image_size-用于训练的图像的空间大小。此实现默认为64x64。如果需要其他尺寸，则必须更改D和G的结构。请参阅这里了解更多详情
nc-输入图像中的颜色通道数。对于彩色图像，这是3
nz-潜在向量的长度
ngf-与生成器承载的特征图的深度有关
ndf-设置通过鉴别器传播的特征图的深度
num_epochs-要运行的训练时期数。训练更长的时间可能会导致更好的结果，但也会花费更长的时间
lr-培训的学习率。如DCGAN文件中所述，此数字应为0.0002
beta1 -beta1超参数，用于Adam优化器。如论文所述，该数字应为0.5
ngpu-可用的GPU数量。如果为0，则代码将在CPU模式下运行。如果此数字大于0，它将在该数量的GPU上运行

# Root directory for dataset
dataroot = "data/celeba"

# Number of workers for dataloader
workers = 2

# Batch size during training
batch_size = 128

# Spatial size of training images. All images will be resized to this
#   size using a transformer.
image_size = 64

# Number of channels in the training images. For color images this is 3
nc = 3

# Size of z latent vector (i.e. size of generator input)
nz = 100

# Size of feature maps in generator
ngf = 64

# Size of feature maps in discriminator
ndf = 64

# Number of training epochs
num_epochs = 5

# Learning rate for optimizers
lr = 0.0002

# Beta1 hyperparam for Adam optimizers
beta1 = 0.5

# Number of GPUs available. Use 0 for CPU mode.
ngpu = 1

Data

在本教程中，我们将使用Celeb-A Faces数据集，该数据集可以在链接的网站或Google Drive中下载。数据集将下载为名为img_align_celeba.zip的文件。下载后，创建一个名为celeba的目录，并将zip文件解压缩到该目录中。然后，将此笔记本的dataroot输入设置为刚创建的celeba目录。结果目录结构应为：

/path/to/celeba-> img_align_celeba-> 188242.jpg-> 173822.jpg-> 284702.jpg-> 537394.jpg...

这是重要的一步，因为我们将使用ImageFolder数据集类，该类要求数据集的根文件夹中有子目录。现在，我们可以创建数据集，创建数据加载器，将设备设置为可以运行，并最终可视化一些训练数据。

# We can use an image folder dataset the way we have it setup.
# Create the dataset
dataset = dset.ImageFolder(root=dataroot,transform=transforms.Compose([transforms.Resize(image_size),transforms.CenterCrop(image_size),transforms.ToTensor(),transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5)),]))
# Create the dataloader
dataloader = torch.utils.data.DataLoader(dataset, batch_size=batch_size,shuffle=True, num_workers=workers)

# Decide which device we want to run on
device = torch.device("cuda:0" if (torch.cuda.is_available() and ngpu > 0) else "cpu")

# Plot some training images
real_batch = next(iter(dataloader))
plt.figure(figsize=(8,8))
plt.axis("off")
plt.title("Training Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=2, normalize=True).cpu(),(1,2,0)))

Implementation

设置好输入参数并准备好数据集后，我们现在可以进入实现了。我们将从weigth初始化策略开始，然后详细讨论生成器，鉴别器，损失函数和训练循环。

Weight Initialization

从DCGAN论文中，作者指定所有模型权重均应从均值= 0，stdev = 0.02的正态分布中随机初始化。该weights_init函数以已初始化的模型作为输入，并重新初始化所有卷积，卷积转置和批处理规范化层，以符合此条件。初始化后立即将此功能应用于模型。

# custom weights initialization called on netG and netD
def weights_init(m):classname = m.__class__.__name__if classname.find('Conv') != -1:nn.init.normal_(m.weight.data, 0.0, 0.02)elif classname.find('BatchNorm') != -1:nn.init.normal_(m.weight.data, 1.0, 0.02)nn.init.constant_(m.bias.data, 0)

Generator

The generator, G

G旨在映射潜在空间矢量（z

z）到数据空间。由于我们的数据是图像，因此转换 z

z到数据空间意味着最终创建具有与训练图像相同大小（即3x64x64）的RGB图像。实际上，这是通过一系列跨步的二维卷积转置层来完成的，每个层都与2d批处理规范层和relu激活配对。生成器的输出通过tanh函数馈送，以使其返回到输入数据范围。[−1,1]

[−1,1]。值得注意的是，在卷积转置层之后存在批处理规范函数，因为这是DCGAN论文的关键贡献。这些层有助于训练过程中的梯度流动。DCGAN纸生成的图像如下所示。

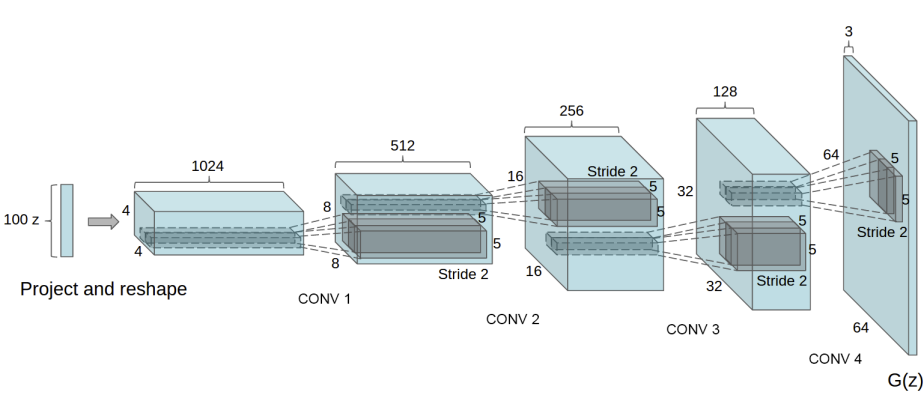
注意，我们在输入部分中设置的输入（nz，ngf和 nc）如何影响代码中的生成器体系结构。nz是z输入向量的长度，ngf与通过生成器传播的特征图的大小有关，nc是输出图像中的通道数（对于RGB图像设置为3）。下面是生成器的代码。

# Generator Code

class Generator(nn.Module):def __init__(self, ngpu):super(Generator, self).__init__()self.ngpu = ngpuself.main = nn.Sequential(# input is Z, going into a convolutionnn.ConvTranspose2d( nz, ngf * 8, 4, 1, 0, bias=False),nn.BatchNorm2d(ngf * 8),nn.ReLU(True),# state size. (ngf*8) x 4 x 4nn.ConvTranspose2d(ngf * 8, ngf * 4, 4, 2, 1, bias=False),nn.BatchNorm2d(ngf * 4),nn.ReLU(True),# state size. (ngf*4) x 8 x 8nn.ConvTranspose2d( ngf * 4, ngf * 2, 4, 2, 1, bias=False),nn.BatchNorm2d(ngf * 2),nn.ReLU(True),# state size. (ngf*2) x 16 x 16nn.ConvTranspose2d( ngf * 2, ngf, 4, 2, 1, bias=False),nn.BatchNorm2d(ngf),nn.ReLU(True),# state size. (ngf) x 32 x 32nn.ConvTranspose2d( ngf, nc, 4, 2, 1, bias=False),nn.Tanh()# state size. (nc) x 64 x 64)
def forward(self, input):return self.main(input)

现在，我们可以实例化生成器并应用weights_init 函数。签出打印的模型以查看生成器对象的结构。

# Create the generator
netG = Generator(ngpu).to(device)

# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):netG = nn.DataParallel(netG, list(range(ngpu)))

# Apply the weights_init function to randomly initialize all weights
#  to mean=0, stdev=0.2.
netG.apply(weights_init)

# Print the model
print(netG)

输出：

Generator((main): Sequential((0): ConvTranspose2d(100, 512, kernel_size=(4, 4), stride=(1, 1), bias=False)(1): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)(2): ReLU(inplace=True)(3): ConvTranspose2d(512, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(4): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)(5): ReLU(inplace=True)(6): ConvTranspose2d(256, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(7): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)(8): ReLU(inplace=True)(9): ConvTranspose2d(128, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(10): BatchNorm2d(64, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)(11): ReLU(inplace=True)(12): ConvTranspose2d(64, 3, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(13): Tanh())
)

Discriminator

如前所述，歧视者 D

D是一个二进制分类网络，它将图像作为输入并输出输入图像是真实的（与假的相对）的标量概率。这里，D

D拍摄3x64x64的输入图像，通过一系列的Conv2d，BatchNorm2d和LeakyReLU层对其进行处理，然后通过Sigmoid激活函数输出最终概率。如果需要解决此问题，可以用更多层扩展此体系结构，但是使用跨步卷积，BatchNorm和LeakyReLU仍然很重要。DCGAN论文提到，使用跨步卷积而不是通过池化来进行下采样是一个好习惯，因为它可以让网络学习自己的池化功能。批处理规范和泄漏的relu函数还可以促进健康的梯度流动，这对于两者的学习过程都至关重要 G

G 和 D

D。

Discriminator Code

class Discriminator(nn.Module):def __init__(self, ngpu):super(Discriminator, self).__init__()self.ngpu = ngpuself.main = nn.Sequential(# input is (nc) x 64 x 64nn.Conv2d(nc, ndf, 4, 2, 1, bias=False),nn.LeakyReLU(0.2, inplace=True),# state size. (ndf) x 32 x 32nn.Conv2d(ndf, ndf * 2, 4, 2, 1, bias=False),nn.BatchNorm2d(ndf * 2),nn.LeakyReLU(0.2, inplace=True),# state size. (ndf*2) x 16 x 16nn.Conv2d(ndf * 2, ndf * 4, 4, 2, 1, bias=False),nn.BatchNorm2d(ndf * 4),nn.LeakyReLU(0.2, inplace=True),# state size. (ndf*4) x 8 x 8nn.Conv2d(ndf * 4, ndf * 8, 4, 2, 1, bias=False),nn.BatchNorm2d(ndf * 8),nn.LeakyReLU(0.2, inplace=True),# state size. (ndf*8) x 4 x 4nn.Conv2d(ndf * 8, 1, 4, 1, 0, bias=False),nn.Sigmoid())
def forward(self, input):return self.main(input)

现在，与生成器一样，我们可以创建鉴别器，应用 weights_init函数并打印模型的结构。

# Create the Discriminator
netD = Discriminator(ngpu).to(device)

# Handle multi-gpu if desired
if (device.type == 'cuda') and (ngpu > 1):netD = nn.DataParallel(netD, list(range(ngpu)))

# Apply the weights_init function to randomly initialize all weights
#  to mean=0, stdev=0.2.
netD.apply(weights_init)

# Print the model
print(netD)

输出：

Discriminator((main): Sequential((0): Conv2d(3, 64, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(1): LeakyReLU(negative_slope=0.2, inplace=True)(2): Conv2d(64, 128, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(3): BatchNorm2d(128, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)(4): LeakyReLU(negative_slope=0.2, inplace=True)(5): Conv2d(128, 256, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(6): BatchNorm2d(256, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)(7): LeakyReLU(negative_slope=0.2, inplace=True)(8): Conv2d(256, 512, kernel_size=(4, 4), stride=(2, 2), padding=(1, 1), bias=False)(9): BatchNorm2d(512, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)(10): LeakyReLU(negative_slope=0.2, inplace=True)(11): Conv2d(512, 1, kernel_size=(4, 4), stride=(1, 1), bias=False)(12): Sigmoid())
)

Loss Functions and Optimizers

用 D

D 和 G

G设置中，我们可以指定他们如何通过损失函数和优化器学习。我们将使用在PyTorch中定义的二进制交叉熵损失（BCELoss）函数：

ℓ(x,y)=L={l

,…,l

}

⊤

=−[y

⋅logx

+(1−y

)⋅log(1−x

)]

ℓ(x,y)=L={l1,…,lN}⊤,ln=−[yn⋅logxn+(1−yn)⋅log(1−xn)]

注意此函数如何提供目标函数中两个日志组件的计算（即 log(D(x))

log(D(x)) 和 log(1−D(G(z)))

log(1−D(G(z)))）。我们可以指定BCE方程的哪一部分与y

y输入。这是在即将到来的训练循环中完成的，但重要的是要了解我们如何通过更改即可选择希望计算的分量y

y （即GT标签）。

接下来，我们将真实标签定义为1，将假标签定义为0。这些标签将在计算损耗时使用 D

D 和 G

G，这也是原始GAN论文中使用的约定。最后，我们设置了两个单独的优化器，其中一个用于D

D 还有一个 G

G。根据DCGAN论文中的说明，这两个都是Adam优化器，学习率均为0.0002，Beta1 = 0.5。为了跟踪生成器的学习进度，我们将生成一批固定的潜矢量，这些矢量是从高斯分布（即fixed_noise）中得出的。在训练循环中，我们将定期将fixed_noise输入到G

G，并且在迭代过程中，我们将看到图像形成于噪声之外。

# Initialize BCELoss function
criterion = nn.BCELoss()

# Create batch of latent vectors that we will use to visualize
#  the progression of the generator
fixed_noise = torch.randn(64, nz, 1, 1, device=device)

# Establish convention for real and fake labels during training
real_label = 1.
fake_label = 0.

# Setup Adam optimizers for both G and D
optimizerD = optim.Adam(netD.parameters(), lr=lr, betas=(beta1, 0.999))
optimizerG = optim.Adam(netG.parameters(), lr=lr, betas=(beta1, 0.999))

Training

最后，既然我们已经定义了GAN框架的所有部分，我们就可以对其进行培训。请注意，训练GAN某种程度上是一种艺术形式，因为不正确的超参数设置会导致模式崩溃，而对失败的原因几乎没有解释。在这里，我们将遵循Goodfellow论文中的算法1，同时遵守ganhacks中显示的一些最佳实践。即，我们将“为真假构建不同的小批量”图像，并调整G的目标函数以最大化 logD(G(z))

logD(G(z))。培训分为两个主要部分。第1部分更新了鉴别器，第2部分更新了生成器。

第1部分-训练鉴别器

回想一下，训练鉴别器的目的是最大程度地提高将给定输入正确分类为真实或伪造的可能性。就古德费罗而言，我们希望“通过增加随机梯度来更新鉴别器”。实际上，我们要最大化 log(D(x))+log(1−D(G(z)))

log(D(x))+log(1−D(G(z)))。由于来自ganhacks的单独的小批量建议，我们将分两步进行计算。首先，我们将从训练集中构造一批真实样本，向前传递D

D，计算损失（log(D(x))

log(D(x))），然后在向后传递中计算梯度。其次，我们将使用电流发生器构造一批假样品，将其通过D

D，计算损失（log(1−D(G(z)))

log(1−D(G(z)))），并通过向后传递来累积梯度。现在，利用从全部真实批次和所有伪批次累积的渐变，我们将其称为鉴别器优化器的一个步骤。

第2部分-训练生成器

如原始文件所述，我们希望通过最小化训练Generator log(1−D(G(z)))

log(1−D(G(z)))为了产生更好的假货。如前所述，Goodfellow证明这不能提供足够的梯度，尤其是在学习过程的早期。作为解决方法，我们希望最大化log(D(G(z)))

log(D(G(z)))。在代码中，我们通过以下方式实现此目的：将第1部分的Generator输出与Discriminator进行分类，使用实数标签GT来计算G的损失，以反向方式计算G的梯度，最后通过优化器步骤更新G的参数。将真实标签用作损失函数的GT标签似乎违反直觉，但这使我们可以使用 log(x)

log(x) BCELoss的一部分（而不是 log(1−x)

log(1−x) 部分）正是我们想要的。

最后，我们将进行一些统计报告，并在每个时期结束时，将我们的fixed_noise批处理推入生成器，以直观地跟踪G的训练进度。报告的培训统计数据是：

Loss_D-鉴别器损失，计算为所有真实批次和所有假批次的损失总和（log(D(x))+log(D(G(z)))

log(D(x))+log(D(G(z)))）。

Loss_G-生成器损耗计算为log(D(G(z)))

log(D(G(z)))
D（x） -所有实际批次的鉴别器的平均输出（整个批次）。这应该从接近1开始，然后在G变得更好时理论上收敛到0.5。想想这是为什么。
D（G（z）） -所有假批次的平均鉴别器输出。第一个数字在D更新之前，第二个数字在D更新之后。这些数字应从0开始，并随着G的提高收敛到0.5。想想这是为什么。

注意：此步骤可能需要一段时间，具体取决于运行了多少个时期以及是否从数据集中删除了一些数据。

# Training Loop# Lists to keep track of progress
img_list = []
G_losses = []
D_losses = []
iters = 0

print("Starting Training Loop...")
# For each epoch
for epoch in range(num_epochs):# For each batch in the dataloaderfor i, data in enumerate(dataloader, 0):############################# (1) Update D network: maximize log(D(x)) + log(1 - D(G(z)))############################# Train with all-real batchnetD.zero_grad()# Format batchreal_cpu = data[0].to(device)b_size = real_cpu.size(0)label = torch.full((b_size,), real_label, dtype=torch.float, device=device)# Forward pass real batch through Doutput = netD(real_cpu).view(-1)# Calculate loss on all-real batcherrD_real = criterion(output, label)# Calculate gradients for D in backward passerrD_real.backward()D_x = output.mean().item()## Train with all-fake batch# Generate batch of latent vectorsnoise = torch.randn(b_size, nz, 1, 1, device=device)# Generate fake image batch with Gfake = netG(noise)label.fill_(fake_label)# Classify all fake batch with Doutput = netD(fake.detach()).view(-1)# Calculate D's loss on the all-fake batcherrD_fake = criterion(output, label)# Calculate the gradients for this batcherrD_fake.backward()D_G_z1 = output.mean().item()# Add the gradients from the all-real and all-fake batcheserrD = errD_real + errD_fake# Update DoptimizerD.step()############################# (2) Update G network: maximize log(D(G(z)))###########################netG.zero_grad()label.fill_(real_label)  # fake labels are real for generator cost# Since we just updated D, perform another forward pass of all-fake batch through Doutput = netD(fake).view(-1)# Calculate G's loss based on this outputerrG = criterion(output, label)# Calculate gradients for GerrG.backward()D_G_z2 = output.mean().item()# Update GoptimizerG.step()# Output training statsif i % 50 == 0:print('[%d/%d][%d/%d]\tLoss_D: %.4f\tLoss_G: %.4f\tD(x): %.4f\tD(G(z)): %.4f / %.4f'% (epoch, num_epochs, i, len(dataloader),errD.item(), errG.item(), D_x, D_G_z1, D_G_z2))# Save Losses for plotting laterG_losses.append(errG.item())D_losses.append(errD.item())# Check how the generator is doing by saving G's output on fixed_noiseif (iters % 500 == 0) or ((epoch == num_epochs-1) and (i == len(dataloader)-1)):with torch.no_grad():fake = netG(fixed_noise).detach().cpu()img_list.append(vutils.make_grid(fake, padding=2, normalize=True))
iter

输出：

Starting Training Loop...
[0/5][0/1583]   Loss_D: 2.0937  Loss_G: 5.2060  D(x): 0.5704    D(G(z)): 0.6680 / 0.0090
[0/5][50/1583]  Loss_D: 0.3205  Loss_G: 28.7176 D(x): 0.8707    D(G(z)): 0.0000 / 0.0000
[0/5][100/1583] Loss_D: 0.5162  Loss_G: 7.7843  D(x): 0.9291    D(G(z)): 0.2372 / 0.0008
[0/5][150/1583] Loss_D: 2.0451  Loss_G: 2.8682  D(x): 0.3193    D(G(z)): 0.0166 / 0.1436
[0/5][200/1583] Loss_D: 0.3517  Loss_G: 6.0990  D(x): 0.9093    D(G(z)): 0.2013 / 0.0044
[0/5][250/1583] Loss_D: 0.7547  Loss_G: 8.5222  D(x): 0.9529    D(G(z)): 0.4535 / 0.0005
[0/5][300/1583] Loss_D: 0.7168  Loss_G: 5.8260  D(x): 0.8828    D(G(z)): 0.3812 / 0.0081
[0/5][350/1583] Loss_D: 1.3500  Loss_G: 1.7561  D(x): 0.3602    D(G(z)): 0.0119 / 0.2361
[0/5][400/1583] Loss_D: 0.2604  Loss_G: 5.1003  D(x): 0.8558    D(G(z)): 0.0576 / 0.0135
[0/5][450/1583] Loss_D: 0.5045  Loss_G: 5.1198  D(x): 0.8478    D(G(z)): 0.2386 / 0.0120
[0/5][500/1583] Loss_D: 0.2465  Loss_G: 4.2570  D(x): 0.9021    D(G(z)): 0.1051 / 0.0281
[0/5][550/1583] Loss_D: 0.7534  Loss_G: 7.7971  D(x): 0.9507    D(G(z)): 0.4235 / 0.0019
[0/5][600/1583] Loss_D: 0.4012  Loss_G: 4.7346  D(x): 0.8224    D(G(z)): 0.1187 / 0.0138
[0/5][650/1583] Loss_D: 0.5906  Loss_G: 8.5123  D(x): 0.8984    D(G(z)): 0.3176 / 0.0007
[0/5][700/1583] Loss_D: 0.9194  Loss_G: 1.9009  D(x): 0.5547    D(G(z)): 0.0482 / 0.2132
[0/5][750/1583] Loss_D: 0.6259  Loss_G: 5.4178  D(x): 0.8645    D(G(z)): 0.3173 / 0.0092
[0/5][800/1583] Loss_D: 0.8920  Loss_G: 2.2508  D(x): 0.6173    D(G(z)): 0.1691 / 0.1600
[0/5][850/1583] Loss_D: 0.5429  Loss_G: 5.7621  D(x): 0.7002    D(G(z)): 0.0168 / 0.0087
[0/5][900/1583] Loss_D: 0.5520  Loss_G: 7.7991  D(x): 0.9592    D(G(z)): 0.3451 / 0.0011
[0/5][950/1583] Loss_D: 0.7994  Loss_G: 2.3076  D(x): 0.6247    D(G(z)): 0.0941 / 0.1728
[0/5][1000/1583]        Loss_D: 1.0630  Loss_G: 3.2791  D(x): 0.4523    D(G(z)): 0.0073 / 0.0931
[0/5][1050/1583]        Loss_D: 0.5231  Loss_G: 4.6262  D(x): 0.8436    D(G(z)): 0.2250 / 0.0166
[0/5][1100/1583]        Loss_D: 0.4547  Loss_G: 6.0315  D(x): 0.9717    D(G(z)): 0.2867 / 0.0059
[0/5][1150/1583]        Loss_D: 0.8126  Loss_G: 3.7971  D(x): 0.6047    D(G(z)): 0.0514 / 0.0641
[0/5][1200/1583]        Loss_D: 0.5976  Loss_G: 6.2676  D(x): 0.9216    D(G(z)): 0.3387 / 0.0045
[0/5][1250/1583]        Loss_D: 0.4574  Loss_G: 3.8314  D(x): 0.8254    D(G(z)): 0.1773 / 0.0362
[0/5][1300/1583]        Loss_D: 0.6985  Loss_G: 4.3205  D(x): 0.7868    D(G(z)): 0.2796 / 0.0316
[0/5][1350/1583]        Loss_D: 0.6255  Loss_G: 2.5133  D(x): 0.6686    D(G(z)): 0.0596 / 0.1319
[0/5][1400/1583]        Loss_D: 0.3427  Loss_G: 3.3193  D(x): 0.9211    D(G(z)): 0.1968 / 0.0624
[0/5][1450/1583]        Loss_D: 0.7543  Loss_G: 1.7941  D(x): 0.5763    D(G(z)): 0.0167 / 0.2470
[0/5][1500/1583]        Loss_D: 0.3236  Loss_G: 2.8982  D(x): 0.8587    D(G(z)): 0.1157 / 0.1147
[0/5][1550/1583]        Loss_D: 0.6168  Loss_G: 5.9430  D(x): 0.9069    D(G(z)): 0.3432 / 0.0058
[1/5][0/1583]   Loss_D: 1.6692  Loss_G: 6.6843  D(x): 0.9681    D(G(z)): 0.7282 / 0.0053
[1/5][50/1583]  Loss_D: 0.2964  Loss_G: 4.3601  D(x): 0.9244    D(G(z)): 0.1574 / 0.0233
[1/5][100/1583] Loss_D: 0.2932  Loss_G: 3.4547  D(x): 0.8499    D(G(z)): 0.0966 / 0.0528
[1/5][150/1583] Loss_D: 0.4235  Loss_G: 4.1534  D(x): 0.8883    D(G(z)): 0.2305 / 0.0230
[1/5][200/1583] Loss_D: 2.4919  Loss_G: 11.5573 D(x): 0.9835    D(G(z)): 0.8285 / 0.0000
[1/5][250/1583] Loss_D: 0.3591  Loss_G: 4.0402  D(x): 0.8719    D(G(z)): 0.1731 / 0.0253
[1/5][300/1583] Loss_D: 0.7471  Loss_G: 6.8861  D(x): 0.9504    D(G(z)): 0.4539 / 0.0018
[1/5][350/1583] Loss_D: 0.4002  Loss_G: 2.8062  D(x): 0.7613    D(G(z)): 0.0682 / 0.1054
[1/5][400/1583] Loss_D: 1.3911  Loss_G: 6.6034  D(x): 0.9758    D(G(z)): 0.6380 / 0.0054
[1/5][450/1583] Loss_D: 0.3840  Loss_G: 3.4407  D(x): 0.8123    D(G(z)): 0.1146 / 0.0516
[1/5][500/1583] Loss_D: 0.7956  Loss_G: 6.0227  D(x): 0.9423    D(G(z)): 0.4406 / 0.0046
[1/5][550/1583] Loss_D: 0.4370  Loss_G: 4.1524  D(x): 0.9055    D(G(z)): 0.2491 / 0.0255
[1/5][600/1583] Loss_D: 0.4104  Loss_G: 4.4360  D(x): 0.8932    D(G(z)): 0.2212 / 0.0201
[1/5][650/1583] Loss_D: 0.5270  Loss_G: 3.0151  D(x): 0.6922    D(G(z)): 0.0800 / 0.0762
[1/5][700/1583] Loss_D: 1.1739  Loss_G: 1.5562  D(x): 0.4379    D(G(z)): 0.0218 / 0.2705
[1/5][750/1583] Loss_D: 0.4532  Loss_G: 3.6883  D(x): 0.8170    D(G(z)): 0.1717 / 0.0391
[1/5][800/1583] Loss_D: 0.6470  Loss_G: 5.5513  D(x): 0.9187    D(G(z)): 0.3928 / 0.0060
[1/5][850/1583] Loss_D: 2.4949  Loss_G: 0.2302  D(x): 0.1653    D(G(z)): 0.0057 / 0.8178
[1/5][900/1583] Loss_D: 0.5650  Loss_G: 3.8986  D(x): 0.8431    D(G(z)): 0.2855 / 0.0290
[1/5][950/1583] Loss_D: 0.6024  Loss_G: 4.5640  D(x): 0.9109    D(G(z)): 0.3531 / 0.0168
[1/5][1000/1583]        Loss_D: 1.5041  Loss_G: 6.1265  D(x): 0.9828    D(G(z)): 0.6864 / 0.0071
[1/5][1050/1583]        Loss_D: 1.0222  Loss_G: 1.0778  D(x): 0.4522    D(G(z)): 0.0283 / 0.4120
[1/5][1100/1583]        Loss_D: 0.5915  Loss_G: 1.6561  D(x): 0.6721    D(G(z)): 0.1165 / 0.2252
[1/5][1150/1583]        Loss_D: 0.4768  Loss_G: 3.0319  D(x): 0.8771    D(G(z)): 0.2548 / 0.0681
[1/5][1200/1583]        Loss_D: 0.5941  Loss_G: 2.0510  D(x): 0.7028    D(G(z)): 0.1558 / 0.1766
[1/5][1250/1583]        Loss_D: 0.5887  Loss_G: 2.5710  D(x): 0.7472    D(G(z)): 0.2094 / 0.1044
[1/5][1300/1583]        Loss_D: 0.5923  Loss_G: 2.1390  D(x): 0.6602    D(G(z)): 0.0868 / 0.1554
[1/5][1350/1583]        Loss_D: 0.4332  Loss_G: 2.6219  D(x): 0.8049    D(G(z)): 0.1615 / 0.1019
[1/5][1400/1583]        Loss_D: 0.6757  Loss_G: 5.1723  D(x): 0.9347    D(G(z)): 0.4113 / 0.0106
[1/5][1450/1583]        Loss_D: 0.9800  Loss_G: 5.5551  D(x): 0.9565    D(G(z)): 0.5384 / 0.0075
[1/5][1500/1583]        Loss_D: 0.5586  Loss_G: 2.1196  D(x): 0.7442    D(G(z)): 0.1838 / 0.1540
[1/5][1550/1583]        Loss_D: 0.4457  Loss_G: 3.2216  D(x): 0.9229    D(G(z)): 0.2819 / 0.0541
[2/5][0/1583]   Loss_D: 1.4882  Loss_G: 4.7907  D(x): 0.9543    D(G(z)): 0.7081 / 0.0149
[2/5][50/1583]  Loss_D: 0.6210  Loss_G: 2.4005  D(x): 0.6549    D(G(z)): 0.0991 / 0.1317
[2/5][100/1583] Loss_D: 0.9395  Loss_G: 0.7794  D(x): 0.4899    D(G(z)): 0.1132 / 0.5341
[2/5][150/1583] Loss_D: 0.6689  Loss_G: 3.4156  D(x): 0.8642    D(G(z)): 0.3692 / 0.0441
[2/5][200/1583] Loss_D: 0.4944  Loss_G: 3.2601  D(x): 0.8638    D(G(z)): 0.2643 / 0.0507
[2/5][250/1583] Loss_D: 0.3918  Loss_G: 2.6126  D(x): 0.8257    D(G(z)): 0.1504 / 0.0960
[2/5][300/1583] Loss_D: 0.9614  Loss_G: 1.1336  D(x): 0.4715    D(G(z)): 0.0372 / 0.3944
[2/5][350/1583] Loss_D: 0.8356  Loss_G: 4.6990  D(x): 0.9479    D(G(z)): 0.4864 / 0.0147
[2/5][400/1583] Loss_D: 0.4425  Loss_G: 3.5099  D(x): 0.8396    D(G(z)): 0.2021 / 0.0467
[2/5][450/1583] Loss_D: 0.6896  Loss_G: 1.3305  D(x): 0.6035    D(G(z)): 0.1007 / 0.3231
[2/5][500/1583] Loss_D: 0.5245  Loss_G: 2.7391  D(x): 0.7363    D(G(z)): 0.1456 / 0.0939
[2/5][550/1583] Loss_D: 0.6281  Loss_G: 3.6181  D(x): 0.8806    D(G(z)): 0.3422 / 0.0435
[2/5][600/1583] Loss_D: 0.5172  Loss_G: 2.0054  D(x): 0.6952    D(G(z)): 0.0979 / 0.1807
[2/5][650/1583] Loss_D: 0.7094  Loss_G: 1.6731  D(x): 0.6808    D(G(z)): 0.2141 / 0.2416
[2/5][700/1583] Loss_D: 0.6077  Loss_G: 3.6806  D(x): 0.8539    D(G(z)): 0.3231 / 0.0357
[2/5][750/1583] Loss_D: 0.5006  Loss_G: 2.6400  D(x): 0.7796    D(G(z)): 0.1906 / 0.0976
[2/5][800/1583] Loss_D: 2.4353  Loss_G: 6.6802  D(x): 0.9717    D(G(z)): 0.8551 / 0.0034
[2/5][850/1583] Loss_D: 0.6672  Loss_G: 2.4882  D(x): 0.7395    D(G(z)): 0.2494 / 0.1056
[2/5][900/1583] Loss_D: 0.6068  Loss_G: 2.0506  D(x): 0.7685    D(G(z)): 0.2541 / 0.1563
[2/5][950/1583] Loss_D: 1.1527  Loss_G: 1.0302  D(x): 0.4045    D(G(z)): 0.0620 / 0.3996
[2/5][1000/1583]        Loss_D: 0.6020  Loss_G: 1.6329  D(x): 0.7008    D(G(z)): 0.1755 / 0.2348
[2/5][1050/1583]        Loss_D: 0.6199  Loss_G: 1.7791  D(x): 0.6823    D(G(z)): 0.1660 / 0.2197
[2/5][1100/1583]        Loss_D: 0.7976  Loss_G: 1.8908  D(x): 0.5932    D(G(z)): 0.1541 / 0.1934
[2/5][1150/1583]        Loss_D: 0.6862  Loss_G: 3.1289  D(x): 0.9255    D(G(z)): 0.4225 / 0.0564
[2/5][1200/1583]        Loss_D: 0.7988  Loss_G: 4.4272  D(x): 0.9237    D(G(z)): 0.4772 / 0.0161
[2/5][1250/1583]        Loss_D: 1.0687  Loss_G: 1.2742  D(x): 0.4386    D(G(z)): 0.0991 / 0.3285
[2/5][1300/1583]        Loss_D: 0.5771  Loss_G: 2.8182  D(x): 0.7593    D(G(z)): 0.2181 / 0.0824
[2/5][1350/1583]        Loss_D: 0.7718  Loss_G: 3.1658  D(x): 0.8418    D(G(z)): 0.4105 / 0.0555
[2/5][1400/1583]        Loss_D: 0.9438  Loss_G: 0.7650  D(x): 0.5081    D(G(z)): 0.1103 / 0.5126
[2/5][1450/1583]        Loss_D: 0.7658  Loss_G: 1.7474  D(x): 0.5299    D(G(z)): 0.0371 / 0.2072
[2/5][1500/1583]        Loss_D: 0.4790  Loss_G: 2.5001  D(x): 0.7908    D(G(z)): 0.1881 / 0.1026
[2/5][1550/1583]        Loss_D: 0.5776  Loss_G: 2.8116  D(x): 0.7785    D(G(z)): 0.2412 / 0.0810
[3/5][0/1583]   Loss_D: 0.5107  Loss_G: 2.0367  D(x): 0.7182    D(G(z)): 0.1241 / 0.1603
[3/5][50/1583]  Loss_D: 1.2004  Loss_G: 0.6006  D(x): 0.3841    D(G(z)): 0.0362 / 0.5931
[3/5][100/1583] Loss_D: 0.7531  Loss_G: 1.4226  D(x): 0.5672    D(G(z)): 0.0963 / 0.2786
[3/5][150/1583] Loss_D: 0.8406  Loss_G: 3.0987  D(x): 0.8807    D(G(z)): 0.4577 / 0.0638
[3/5][200/1583] Loss_D: 0.5282  Loss_G: 2.2354  D(x): 0.8327    D(G(z)): 0.2651 / 0.1329
[3/5][250/1583] Loss_D: 0.7975  Loss_G: 1.4158  D(x): 0.5521    D(G(z)): 0.0993 / 0.2936
[3/5][300/1583] Loss_D: 1.3589  Loss_G: 0.6487  D(x): 0.3274    D(G(z)): 0.0346 / 0.5589
[3/5][350/1583] Loss_D: 0.9727  Loss_G: 3.9226  D(x): 0.8713    D(G(z)): 0.5184 / 0.0282
[3/5][400/1583] Loss_D: 1.1099  Loss_G: 0.5595  D(x): 0.4051    D(G(z)): 0.0372 / 0.6044
[3/5][450/1583] Loss_D: 0.5090  Loss_G: 2.1603  D(x): 0.7081    D(G(z)): 0.0958 / 0.1467
[3/5][500/1583] Loss_D: 1.2076  Loss_G: 2.8912  D(x): 0.7924    D(G(z)): 0.5469 / 0.0767
[3/5][550/1583] Loss_D: 0.6213  Loss_G: 2.8187  D(x): 0.8121    D(G(z)): 0.2978 / 0.0788
[3/5][600/1583] Loss_D: 1.5132  Loss_G: 0.7452  D(x): 0.2810    D(G(z)): 0.0199 / 0.5200
[3/5][650/1583] Loss_D: 0.6325  Loss_G: 1.9908  D(x): 0.7332    D(G(z)): 0.2332 / 0.1621
[3/5][700/1583] Loss_D: 0.4700  Loss_G: 2.3768  D(x): 0.8017    D(G(z)): 0.1961 / 0.1127
[3/5][750/1583] Loss_D: 0.4660  Loss_G: 1.9785  D(x): 0.7454    D(G(z)): 0.1314 / 0.1671
[3/5][800/1583] Loss_D: 0.8236  Loss_G: 1.5759  D(x): 0.5149    D(G(z)): 0.0574 / 0.2659
[3/5][850/1583] Loss_D: 0.6447  Loss_G: 2.4435  D(x): 0.8134    D(G(z)): 0.3123 / 0.1183
[3/5][900/1583] Loss_D: 0.8042  Loss_G: 2.9455  D(x): 0.7165    D(G(z)): 0.3159 / 0.0749
[3/5][950/1583] Loss_D: 0.4797  Loss_G: 1.8912  D(x): 0.7421    D(G(z)): 0.1403 / 0.1843
[3/5][1000/1583]        Loss_D: 0.5966  Loss_G: 2.0199  D(x): 0.7243    D(G(z)): 0.1975 / 0.1613
[3/5][1050/1583]        Loss_D: 0.5850  Loss_G: 2.6337  D(x): 0.8074    D(G(z)): 0.2703 / 0.0967
[3/5][1100/1583]        Loss_D: 0.5862  Loss_G: 2.3304  D(x): 0.7183    D(G(z)): 0.1794 / 0.1227
[3/5][1150/1583]        Loss_D: 0.9754  Loss_G: 4.6639  D(x): 0.9066    D(G(z)): 0.5346 / 0.0139
[3/5][1200/1583]        Loss_D: 0.9510  Loss_G: 4.2513  D(x): 0.8916    D(G(z)): 0.5185 / 0.0216
[3/5][1250/1583]        Loss_D: 0.8178  Loss_G: 3.2848  D(x): 0.8296    D(G(z)): 0.4206 / 0.0517
[3/5][1300/1583]        Loss_D: 0.5632  Loss_G: 2.0615  D(x): 0.6424    D(G(z)): 0.0618 / 0.1552
[3/5][1350/1583]        Loss_D: 1.1599  Loss_G: 0.3401  D(x): 0.3808    D(G(z)): 0.0480 / 0.7333
[3/5][1400/1583]        Loss_D: 0.8698  Loss_G: 1.2470  D(x): 0.5252    D(G(z)): 0.0950 / 0.3373
[3/5][1450/1583]        Loss_D: 0.6205  Loss_G: 3.7832  D(x): 0.8950    D(G(z)): 0.3603 / 0.0299
[3/5][1500/1583]        Loss_D: 0.4386  Loss_G: 2.3176  D(x): 0.7351    D(G(z)): 0.0955 / 0.1229
[3/5][1550/1583]        Loss_D: 0.6592  Loss_G: 3.4145  D(x): 0.8780    D(G(z)): 0.3693 / 0.0453
[4/5][0/1583]   Loss_D: 1.1703  Loss_G: 4.8790  D(x): 0.9543    D(G(z)): 0.6000 / 0.0128
[4/5][50/1583]  Loss_D: 0.8774  Loss_G: 1.1620  D(x): 0.4962    D(G(z)): 0.0486 / 0.3590
[4/5][100/1583] Loss_D: 0.9925  Loss_G: 4.1293  D(x): 0.9030    D(G(z)): 0.5385 / 0.0290
[4/5][150/1583] Loss_D: 1.1040  Loss_G: 0.7719  D(x): 0.4083    D(G(z)): 0.0401 / 0.5187
[4/5][200/1583] Loss_D: 1.5109  Loss_G: 4.9404  D(x): 0.8857    D(G(z)): 0.6812 / 0.0111
[4/5][250/1583] Loss_D: 0.4348  Loss_G: 2.8826  D(x): 0.7297    D(G(z)): 0.0831 / 0.0828
[4/5][300/1583] Loss_D: 1.0041  Loss_G: 4.2862  D(x): 0.8374    D(G(z)): 0.5067 / 0.0193
[4/5][350/1583] Loss_D: 0.9134  Loss_G: 2.0190  D(x): 0.4813    D(G(z)): 0.0568 / 0.1836
[4/5][400/1583] Loss_D: 0.4618  Loss_G: 2.6098  D(x): 0.7114    D(G(z)): 0.0770 / 0.0987
[4/5][450/1583] Loss_D: 0.7174  Loss_G: 4.2919  D(x): 0.9091    D(G(z)): 0.4184 / 0.0191
[4/5][500/1583] Loss_D: 0.8457  Loss_G: 3.0220  D(x): 0.8611    D(G(z)): 0.4413 / 0.0713
[4/5][550/1583] Loss_D: 0.4782  Loss_G: 3.3955  D(x): 0.8264    D(G(z)): 0.2141 / 0.0487
[4/5][600/1583] Loss_D: 0.4827  Loss_G: 2.4611  D(x): 0.8262    D(G(z)): 0.2181 / 0.1069
[4/5][650/1583] Loss_D: 0.7450  Loss_G: 1.9194  D(x): 0.6449    D(G(z)): 0.1988 / 0.1828
[4/5][700/1583] Loss_D: 0.4777  Loss_G: 2.9116  D(x): 0.8541    D(G(z)): 0.2472 / 0.0694
[4/5][750/1583] Loss_D: 0.6265  Loss_G: 2.3336  D(x): 0.6408    D(G(z)): 0.1119 / 0.1356
[4/5][800/1583] Loss_D: 0.4782  Loss_G: 2.2754  D(x): 0.7747    D(G(z)): 0.1635 / 0.1378
[4/5][850/1583] Loss_D: 0.7227  Loss_G: 2.8305  D(x): 0.7430    D(G(z)): 0.3014 / 0.0798
[4/5][900/1583] Loss_D: 0.6669  Loss_G: 1.4440  D(x): 0.6702    D(G(z)): 0.1792 / 0.2780
[4/5][950/1583] Loss_D: 0.9131  Loss_G: 3.8968  D(x): 0.8929    D(G(z)): 0.5070 / 0.0299
[4/5][1000/1583]        Loss_D: 0.6018  Loss_G: 1.8648  D(x): 0.7068    D(G(z)): 0.1774 / 0.1881
[4/5][1050/1583]        Loss_D: 1.0117  Loss_G: 0.7610  D(x): 0.4501    D(G(z)): 0.0896 / 0.5185
[4/5][1100/1583]        Loss_D: 0.8748  Loss_G: 3.7112  D(x): 0.7815    D(G(z)): 0.4056 / 0.0345
[4/5][1150/1583]        Loss_D: 0.7038  Loss_G: 1.2810  D(x): 0.6005    D(G(z)): 0.1107 / 0.3330
[4/5][1200/1583]        Loss_D: 0.5476  Loss_G: 2.0547  D(x): 0.7042    D(G(z)): 0.1249 / 0.1640
[4/5][1250/1583]        Loss_D: 0.5944  Loss_G: 2.5092  D(x): 0.8397    D(G(z)): 0.3007 / 0.1130
[4/5][1300/1583]        Loss_D: 0.5684  Loss_G: 2.8073  D(x): 0.8774    D(G(z)): 0.3161 / 0.0790
[4/5][1350/1583]        Loss_D: 0.7966  Loss_G: 1.0109  D(x): 0.5672    D(G(z)): 0.1125 / 0.4075
[4/5][1400/1583]        Loss_D: 0.5799  Loss_G: 3.8328  D(x): 0.9027    D(G(z)): 0.3403 / 0.0304
[4/5][1450/1583]        Loss_D: 0.5915  Loss_G: 2.1555  D(x): 0.6472    D(G(z)): 0.0892 / 0.1574
[4/5][1500/1583]        Loss_D: 0.6178  Loss_G: 1.8488  D(x): 0.6610    D(G(z)): 0.1198 / 0.2050
[4/5][1550/1583]        Loss_D: 0.7169  Loss_G: 4.1450  D(x): 0.8530    D(G(z)): 0.3815 / 0.0218

Results

最后，让我们看看我们是如何做到的。在这里，我们将看三个不同的结果。首先，我们将了解D和G的损失在训练过程中如何变化。其次，我们将在每个时期将G的输出显示在fixed_noise批次上。第三，我们将查看一批真实数据以及来自G的一批伪数据。

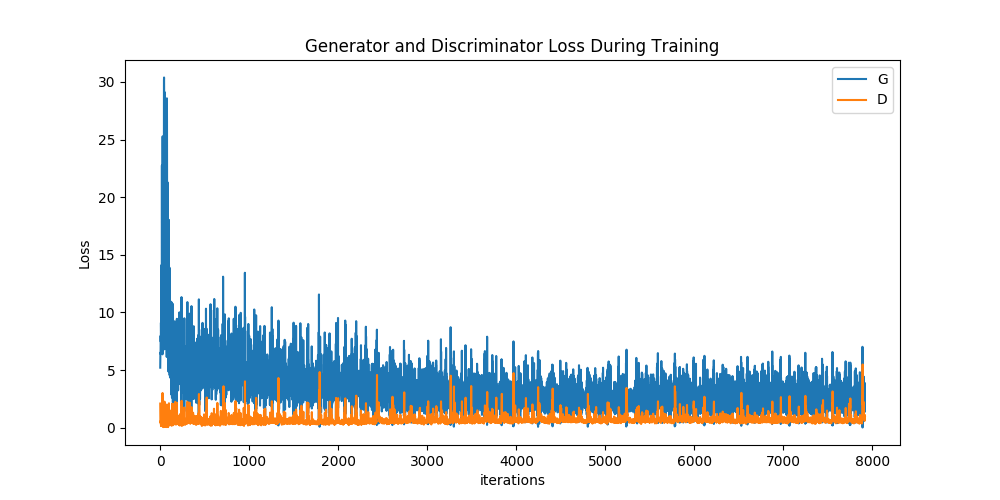
Loss versus training iteration

下面是D＆G的损失与训练迭代的关系图。

plt.figure(figsize=(10,5))
plt.title("Generator and Discriminator Loss During Training")
plt.plot(G_losses,label="G")
plt.plot(D_losses,label="D")
plt.xlabel("iterations")
plt.ylabel("Loss")
plt.legend()
plt.show()

Visualization of G’s progression

请记住，在每次训练之后，我们如何将生成器的输出保存为fixed_noise批次。现在，我们可以用动画可视化G的训练进度。按下播放按钮开始动画。

#%%capture
fig = plt.figure(figsize=(8,8))
plt.axis("off")
ims = [[plt.imshow(np.transpose(i,(1,2,0)), animated=True)] for i in img_list]
ani = animation.ArtistAnimation(fig, ims, interval=1000, repeat_delay=1000, blit=True)

HTML(ani.to_jshtml())

Real Images vs. Fake Images

最后，让我们并排查看一些真实图像和伪图像。

# Grab a batch of real images from the dataloader
real_batch = next(iter(dataloader))

# Plot the real images
plt.figure(figsize=(15,15))
plt.subplot(1,2,1)
plt.axis("off")
plt.title("Real Images")
plt.imshow(np.transpose(vutils.make_grid(real_batch[0].to(device)[:64], padding=5, normalize=True).cpu(),(1,2,0)))

# Plot the fake images from the last epoch
plt.subplot(1,2,2)
plt.axis("off")
plt.title("Fake Images")
plt.imshow(np.transpose(img_list[-1],(1,2,0)))
plt.show()