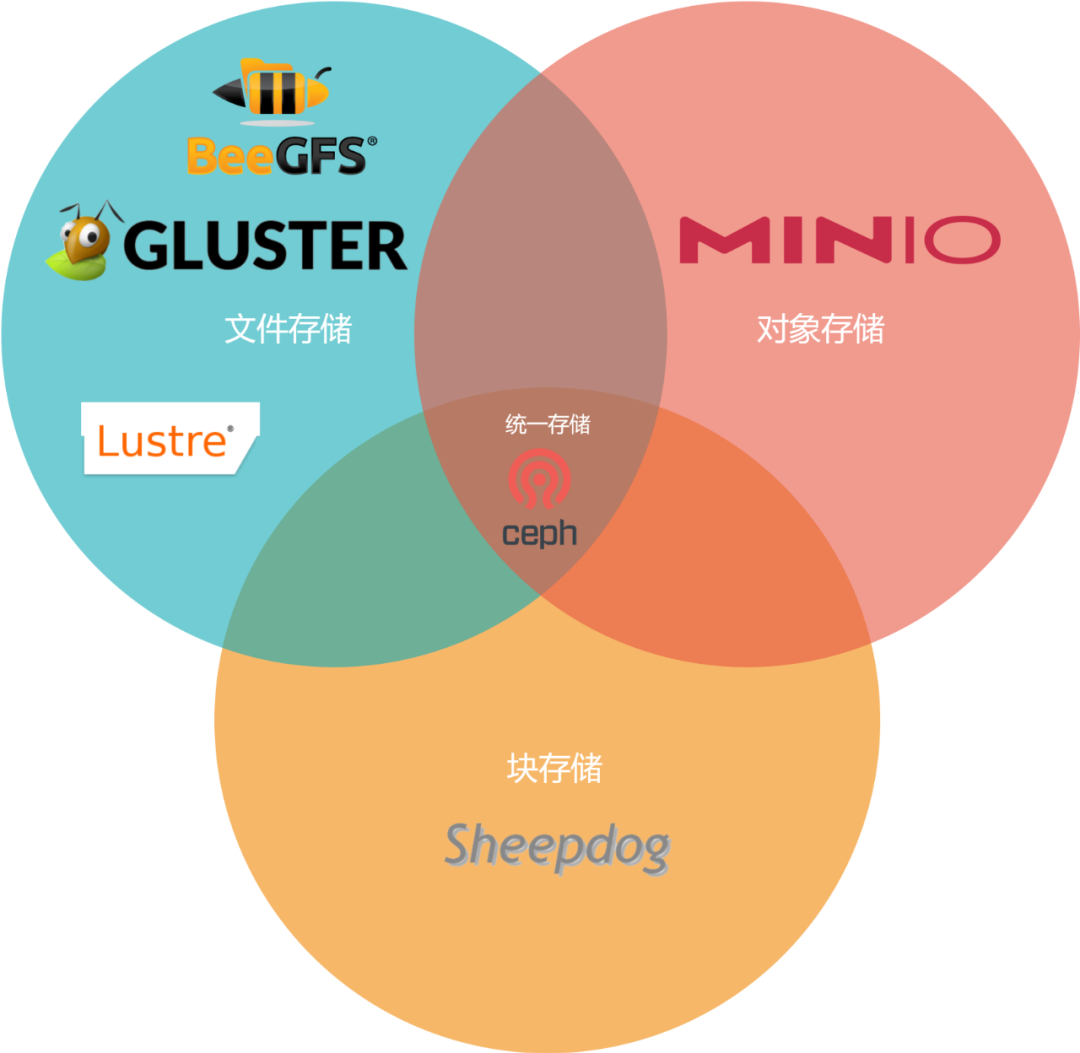
软件定义存储的特征

1 可扩展性

软件定义存储可从传统三节点扩展为数千节点，随着存储设备数量的逐渐递增，软件定义存储内部吞吐量也会不断增加，各项存储性能呈现出线性扩展性能，确保信息可允许群集中的应用控制及访问。

2 弹性

软件定义存储可在用户特定需求的情况下调整容量计算，使数据自动平衡。同时，以较小或较大增量进行数据添加或删除操作，简化容量规划流程，更好控制数据存储成本。

3 虚拟化

软件定义存储虚拟化特征主要体现在借助软件剥离及功能集合等方式将不同异构存储资源组合成同一共享存储系统等方面。在此存储系统中的设备及容量均可被外部应用控制及使用。

软件定义存储如何工作

传统的旧式存储都为单体式存储。它会与硬件（往往都符合行业标准）和专有软件进行捆绑销售。但是，SDS 之所以实用是因为其独立于任何特定硬件。

SDS 并没有将存储空间本身与硬件分隔开。更确切地说，SDS 只不过是一个技术堆栈层，可以使用行业标准服务器（而非专有硬件）来提供大量服务。实际上，SDS 所抽象的对象是用于控制存储请求的组件，而非实际存储的内容。它是位于物理存储和数据请求之间的一个软件层，允许您操控数据的存储方式和存储位置。SDS 控制器软件可以提供存储访问服务、网络和连接。SDS 控制器软件最重要的一个特性是，它不会对底层硬件的容量或有用性做任何假设。