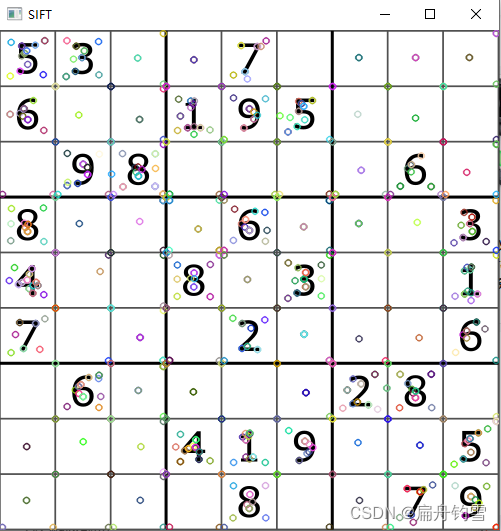
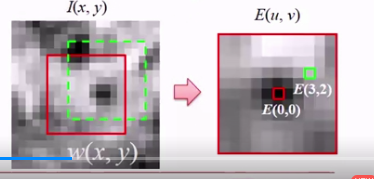
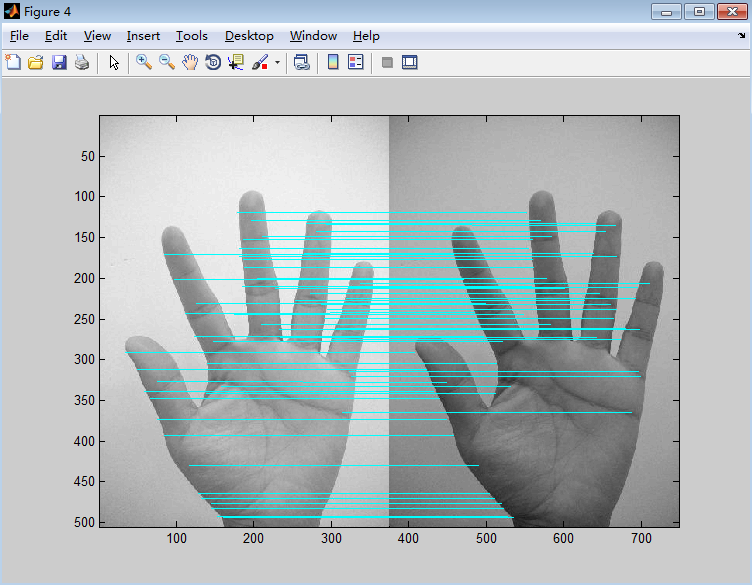
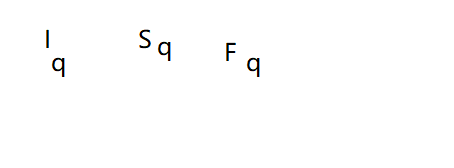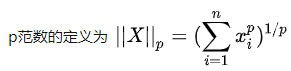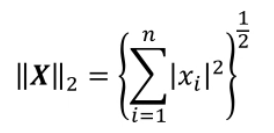sfm算法之三角化(三角测量)

article/2025/9/30 22:45:25

        sfm算法流程一般是特征点提取、特征点匹配、计算本质矩阵/基础矩阵，最后三角化。但是利用机械臂去观察周围，前后帧姿态变化参数是具有的，所以不需要通过基础矩阵获取。

        即利用机械臂的信息直接进行深度估计。已知：手眼标定、相机外参（利用机械臂可获取）、两次拍摄图片目标的像素位置。求目标深度。目前从几次测试来看，效果还是可信的，具体误差没有评估。

        利用的公式如下：

 

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time        :2022/7/27 14:59
# @Author      :weiz
# @ProjectName :robotVision3
# @File        :triangulation.py
# @Description :
import cv2from triangulation_data import *
import mathdef get_M(R, t):"""获取旋转平移的矩阵:param R::param t::return:"""M = [[R[0][0], R[0][1], R[0][2], t[0]],[R[1][0], R[1][1], R[1][2], t[1]],[R[2][0], R[2][1], R[2][2], t[2]]]return np.array(M)def get_M_homo(R, t):"""获取旋转平移的齐次矩阵:param R::param t::return:"""M = [[R[0][0], R[0][1], R[0][2], t[0]],[R[1][0], R[1][1], R[1][2], t[1]],[R[2][0], R[2][1], R[2][2], t[2]],[0,       0,       0,       1]]return np.array(M)def get_world2point2_R_t(R_camera2gripper, t_camera2gripper, point1_gripper, point2_gripper):"""获取关键点1坐标系到关键点2坐标系的 R,t:param R_camera2gripper:手眼标定的R:param t_camera2gripper:手眼标定的t:param point1_gripper:视点1时刻机械臂末端的位姿[x,y,z,rx,ry,rz]:param point2_gripper:视点2时刻机械臂末端的位姿[x,y,z,rx,ry,rz]:return:"""R_gripper2base_point1 = np.zeros((3, 3))t_gripper2base_point1 = np.array([point1_gripper[0], point1_gripper[1], point1_gripper[2]])cv2.Rodrigues(np.array([point1_gripper[3], point1_gripper[4], point1_gripper[5]]), R_gripper2base_point1)R_gripper2base_point2 = np.zeros((3, 3))t_gripper2base_point2 = np.array([point2_gripper[0], point2_gripper[1], point2_gripper[2]])cv2.Rodrigues(np.array([point2_gripper[3], point2_gripper[4], point2_gripper[5]]), R_gripper2base_point2)R_gripper2camera = np.linalg.inv(np.array(R_camera2gripper))t_gripper2camera = -np.dot(R_gripper2camera, t_camera2gripper)R_base2gripper_point2 = np.linalg.inv(np.array(R_gripper2base_point2))t_base2gripper_point2 = -np.dot(R_base2gripper_point2, t_gripper2base_point2)M = get_M_homo(R_camera2gripper, t_camera2gripper)M = np.matmul(get_M_homo(R_gripper2base_point1, t_gripper2base_point1), M)M = np.matmul(get_M_homo(R_base2gripper_point2, t_base2gripper_point2), M)M = np.matmul(get_M_homo(R_gripper2camera, t_gripper2camera), M)R_world2point2 = M[0:3, 0:3]t_world2point2 = np.array([M[0][3], M[1][3], M[2][3]])# print(M)# print(R_world2point2)# print(t_world2point2)return R_world2point2, t_world2point2, Mdef triangulation(point1, point2, ipm, R_world2point2, t_world2point2):"""三角测量：利用机械臂位姿信息直接进行三维坐标估计:param point1:该坐标系为世界坐标系:param point2::param ipm:相机内参:param R_world2point2::param t_world2point2::return:"""ipm = np.array(ipm)M1 = np.matmul(ipm, get_M(np.eye(3, 3), [0, 0, 0]))M2 = np.matmul(ipm, get_M(R_world2point2, t_world2point2))A = []A.append(point1[0] * M1[2] - M1[0])A.append(point1[1] * M1[2] - M1[1])A.append(point2[0] * M2[2] - M2[0])A.append(point2[1] * M2[2] - M2[1])# print(np.array(A))U, sigma, V = np.linalg.svd(A)p_1 = [V[3][0], V[3][1], V[3][2], V[3][3]]p_2 = [V[3][0] / V[3][3], V[3][1] / V[3][3], V[3][2] / V[3][3]]# print(p_1)# print(p_2)total_error = 0point1_pro, _ = cv2.projectPoints(np.array([p_2]), np.eye(3), np.array([[0.], [0.], [0.]]), ipm, None)point2_pro, _ = cv2.projectPoints(np.array([p_2]), R_world2point2, t_world2point2, ipm, None)print(point2_pro)total_error = total_error + cv2.norm(np.array([[point1]], dtype=np.double), point1_pro, cv2.NORM_L2) / 1.total_error = total_error + cv2.norm(np.array([[point1]], dtype=np.float64), point2_pro, cv2.NORM_L2) / 1.print(total_error)return p_2def triangulation_opencv(point1, point2, ipm, R_world2point2, t_world2point2):point1 = np.array([point1], dtype=np.float32)point2 = np.array([point2], dtype=np.float32)M1 = np.zeros((3, 4))M2 = np.zeros((3, 4))M1[0:3, 0:3] = np.eye(3)M2[0:3, 0:3] = np.float32(R_world2point2)M2[:, 3] = np.float32(t_world2point2)M1 = np.matmul(ipm, M1)M2 = np.matmul(ipm, M2)p_homo = cv2.triangulatePoints(M1, M2, point1.T, point2.T)p = []# 齐次坐标转三维坐标：前三个维度除以第四个维度for i in range(len(p_homo[0])):col = p_homo[:, i]col /= col[3]p.append([col[0], col[1], col[2]])return p[0]R_camera2gripper =[[-0.999266726198567, -0.016016251269208765, -0.0347777171142492],[-0.03487664683144269, 0.005939423009193905, 0.99937397542667],[-0.015799665129108013, 0.9998540908300567, -0.00649366092498505]]
t_camera2gripper = [0.057164748537088694, 0.10581519613132581, 0.1255394553568957]
ipm = np.array([[535.05, 0, 653.005], [0, 535.01, 386.191], [0, 0, 1]])
if __name__ == "__main__":R_world2point2, t_world2point2, M = get_world2point2_R_t(R_camera2gripper, t_camera2gripper, point1_gripper, point2_gripper)p = triangulation(point1, point2, ipm, R_world2point2, t_world2point2)print(p)p = triangulation_opencv(point1, point2, ipm, R_world2point2, t_world2point2)print(p)

数据：

#!/usr/bin/env python
# -*- coding: utf-8 -*-
# @Time        :2022/7/29 9:28
# @Author      :weiz
# @ProjectName :Sfm-python-master
# @File        :triangulation_data.py
# @Description :
# Copyright (C) 2021-2025 Jiangxi Institute Of Intelligent Industry Technology Innovation
import numpy as nppoint1 = [738, 389]  # 0.5410932
point1_gripper = [0.5122332451863898, 0.5128182769039566, 0.9630757531852082, -0.7115522167741687, -1.7916510038378088, 1.7013068394360287]
point2 = [797, 374]
point2_gripper = [0.3820852469525631, 0.5235437570806256, 0.9711089613285708, -0.7071726699555351, -1.9459688091738208, 1.7263544531858268]# point1 = [797, 374]  # 0.54940385
# point1_gripper = [0.3820852469525631, 0.5235437570806256, 0.9711089613285708, -0.7071726699555351, -1.9459688091738208, 1.7263544531858268]
# point2 = [715, 343]
# point2_gripper = [0.5056936674804589, 0.4650883838281726, 1.0634729391460807, -0.6999271853483486, -1.749012465435611, 1.6882826312357782]# point1 = [715, 343]  # 0.64878213
# point1_gripper = [0.5056936674804589, 0.4650883838281726, 1.0634729391460807, -0.6999271853483486, -1.749012465435611, 1.6882826312357782]
# point2 = [733, 368]
# point2_gripper = [0.5485518509025477, 0.5157901201998042, 0.9837568437877331, -0.6609672121210775, -1.7084733902118903, 1.7261963960916609]# point1 = [733, 368]  # 0.5727386
# point1_gripper = [0.5485518509025477, 0.5157901201998042, 0.9837568437877331, -0.6609672121210775, -1.7084733902118903, 1.7261963960916609]
# point2 = [738, 389]
# point2_gripper = [0.5122332451863898, 0.5128182769039566, 0.9630757531852082, -0.7115522167741687, -1.7916510038378088, 1.7013068394360287]def pixel_normalization(point1, point2):points_norm = []points_norm.append(point1)points_norm.append(point2)points_norm = np.array(points_norm)points_norm = (points_norm - np.mean(points_norm)) / np.std(points_norm)return points_norm[0], points_norm[1]if __name__ == "__main__":p1, p2 = pixel_normalization(point1, point2)print(p1)print(p2)


http://chatgpt.dhexx.cn/article/Ji19cElF.shtml

相关文章

简述人脸识别技术

简述人脸识别技术

简介 人脸识别技术是一种生物识别技术，可以用来确认用户身份。人脸识别技术相比于传统的身份识别技术有很大的优势，主要体现在方便性上。传统的身份认证方式诸如：密码、PIN码、射频卡片、口令、指纹等，需要用户记住复杂密码或者携…
阅读更多...
Python机器视觉--OpenCV进阶(核心)-边缘检测之SIFT关键点检测

Python机器视觉--OpenCV进阶(核心)-边缘检测之SIFT关键点检测

SIFT关键点检测 SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。 …
阅读更多...
图像特征与描述子（直方图， 聚类， 边缘检测， 兴趣点/关键点， Harris角点， 斑点（Blob), SIFI, 纹理特征）...

图像特征与描述子（直方图， 聚类， 边缘检测， 兴趣点/关键点， Harris角点， 斑点（Blob), SIFI, 纹理特征）...

1.直方图 用于计算图片特征，表达， 使得数据具有总结性， 颜色直方图对数据空间进行量化，好比10个bin 2. 聚类 类内对象的相关性高 类间对象的相关性差 常用算法：kmeans， EM算法， meanshift&#…
阅读更多...
SIFI尺度不变特征变换算法

SIFI尺度不变特征变换算法

SIFT 尺度不变特征变换算法 David Lowe关于Sfit算法，2004年发表在Int. Journal of Computer Vision的经典论文中，对尺度空间（scal space)是这样定义的 ： It has been shown by Koenderink (1984) and Lindeberg (1994) that un…
阅读更多...
Opencv图像识别从零到精通（34）---SIFI

Opencv图像识别从零到精通（34）---SIFI

一、理论知识 Scale Invariant Feature Transform，尺度不变特征变换匹配算法，对于算法的理论介绍，可以参考这篇文章http://blog.csdn.net/qq_20823641/article/details/51692415，里面很详细，可以更好的学习。这里就不多…
阅读更多...
32-SIFI特征点提取（EmguCV学习）

32-SIFI特征点提取（EmguCV学习）

文章目录 RecordCode效果 Record 1、特征点检测与匹配常用的算法：FAST（FastFeatureDetector）、STAR（StarFeatureDetector）、SIFT、SURF、ORB、MSER、GFTT（GoodFeaturesToTrackDetector）、HARRI…
阅读更多...
SIFI特征点提取

SIFI特征点提取

尺度不变特征变换匹配算法详解 Scale Invariant Feature Transform(SIFT) Just For Fun zdd zddmailgmail.com 对于初学者，从David G.Lowe的论文到实现，有许多鸿沟，本文帮你跨越。 1、SIFT综述 尺度不变特征转换(Scale-invariant feature tr…
阅读更多...
图像SIFI笔记

图像SIFI笔记

Image/userl representation > down screen tasks 端到端的 文本领域 字典 visual word本质是 local feature handcraft feature 希望这个具有足够的泛华性 generalize 为了有交集 泛化性 clustering 聚类 Quantization 量化 每张图像 有特征点 local feature sift(128d维…
阅读更多...
特征点匹配(SIFI)

特征点匹配(SIFI)

1.SIFI https://blog.csdn.net/weixin_38404120/article/details/73740612（参考了这个作者的内容） 结合书上加博客的内容进行理解； 求取SIFI特征的步骤： 首先要对图像归一化，然后将图像扩大为原来的两倍&#xff0…
阅读更多...
SIFI和ORB在尺度缩放、旋转、仿射上的特征点不变实验代码，并比较SIFI和ORB提取特征点的速度

SIFI和ORB在尺度缩放、旋转、仿射上的特征点不变实验代码，并比较SIFI和ORB提取特征点的速度

SIFI和ORB在尺度缩放、旋转、仿射上的特征点不变 一、SIFI算法1.验证旋转不变性2.验证尺度不变性3.验证仿射不变性 对原图进行仿射变换并输出 二、ORB算法1.验证旋转不变性2.验证尺度不变性3.验证仿射不变性 对原图进行仿射变换并输出 三、比较SIFT和ORB的尺度旋转，…
阅读更多...
向量范数简述

向量范数简述

向量范数：表征在向量空间中向量的大小 一般表示：,其中X是n维向量，一般如果省略下面的p且无特别说明的话，指的就是2范数，也叫欧几里得范数。对向量来说，就是指向量的模。 常用的向量范数： 0范…
阅读更多...
欧几里得范数/欧几里得距离(L2范数)

欧几里得范数/欧几里得距离(L2范数)

首先m维空间的概念: Rm的距离结构: 2维平面空间: m维空间: 范形空间距离 n维矢量空间中的元素X的Lp范数: 其中X是一连串的向量 最常用的是L2范数: 本质是一个距离概念 参考:《数学分析》
阅读更多...
概念理解_L2范数（欧几里得范数）

概念理解_L2范数（欧几里得范数）

L2范数 L2范数、欧几里得范数一些概念。 首先，明确一点，常用到的几个概念，含义相同。 欧几里得范数（Euclidean norm） 欧式长度 L2 范数 L2距离 Euclidean norm Euclidean length L2 norm L2 distance norm 对于一…
阅读更多...
0范数，1范数，欧几里得范数等范数总结

0范数，1范数，欧几里得范数等范数总结

以下分别列举常用的向量范数和矩阵范数的定义。 向量范数 1-范数： 即向量元素绝对值之和，matlab调用函数norm(x, 1) 。 2-范数： Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值…
阅读更多...
范数、正则化、归一化、标准化

范数、正则化、归一化、标准化

在总结正则化（Regularization）之前，我们先谈一谈正则化是什么，为什么要正则化。 个人认为正则化这个字眼有点太过抽象和宽泛，其实正则化的本质很简单，就是对某一问题加以先验的限制或约束以达到某种特定目的…
阅读更多...
常见向量范数和矩阵范数

常见向量范数和矩阵范数

1、向量范数 1-范数：，即向量元素绝对值之和，matlab调用函数norm(x, 1) 。 2-范数：，Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方&#xf…
阅读更多...
欧氏距离,l2范数,l2-loss,l2正则化

欧氏距离,l2范数,l2-loss,l2正则化

欧式距离,l2范数,l2-loss,l2正则化 1.欧氏距离2.L2范数范数计算公式L1范数L2范数在机器学习方面的区别为什么L2范数可以防止过拟合? 3.L2-Loss4.L2正则化正则化L2正则化 参考文献 1.欧氏距离 距离度量（Distance）用于衡量个体在空间上存在的距离&#x…
阅读更多...
pytorch求范数函数——torch.norm

pytorch求范数函数——torch.norm

torch.norm(input, pfro, dimNone, keepdimFalse, outNone, dtypeNone) 返回所给定tensor的矩阵范数或向量范数,所谓范数也就是把一个高纬度的东西,压缩成为一个大于等于零的数,用以估算这里东西的大小(幅度) 参数： input：输入tensorp (int, float, i…
阅读更多...
来自知乎的范数理解

来自知乎的范数理解

以下分别列举常用的向量范数和矩阵范数的定义。 向量范数 1-范数： ，即向量元素绝对值之和，matlab调用函数norm(x, 1) 。 2-范数： ，Euclid范数（欧几里得范数，常用计算向量长度）&…
阅读更多...
16.1 几何空间

16.1 几何空间

文章目录 1 欧几里得范数2 距离3 标准内积5 夹角与正交6 叉乘7 平行四边形法则8 欧几里得运动 几何空间是用线性代数解决几何问题的一类空间，这是线性代数学习绕不过去的槛。几何空间，学习起来我觉得吧，主要是三个点：内积、长度、…
阅读更多...
推荐文章

Copyright @ 2022~2023