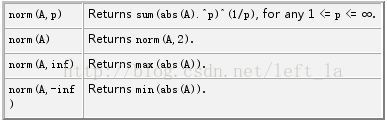
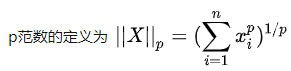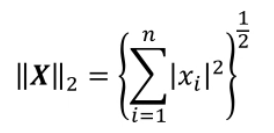SIFT关键点检测

SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。

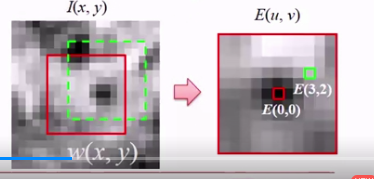
Harris角点具有旋转不变的特性.但是缩放后, 原来的角点有可能就不是角点了.

SIFT可以应用到物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对等方向。

• SIFT算法的特点:

  • 稳定性
  • 独特性
  • 多量性
  • 高速性
  • 可扩展性

• SIFT算法可以的解决问题：

  • 目标的旋转、缩放、平移（RST）
  • 图像放射/投影变换（视点viewpoint）
  • 光照影响（illumination）
  • 部分目标遮挡（occlusion）
  • 杂物场景（clutter）
  • 噪声

1. SIFT原理

1.1 图像尺度空间

• SIFT 第一步就是寻找尺度空间的极值

在一定的范围内，无论物体是大还是小，人眼都可以分辨出来，然而计算机要有相同的能力却很难，所以要让机器能够对物体在不同尺度下有一个统一的认知，就需要考虑图像在不同的尺度下都存在的特点。

尺度空间的获取通常使用高斯模糊来实现

不同σ的高斯函数决定了对图像的平滑程度，越大的σ值对应的图像越模糊。

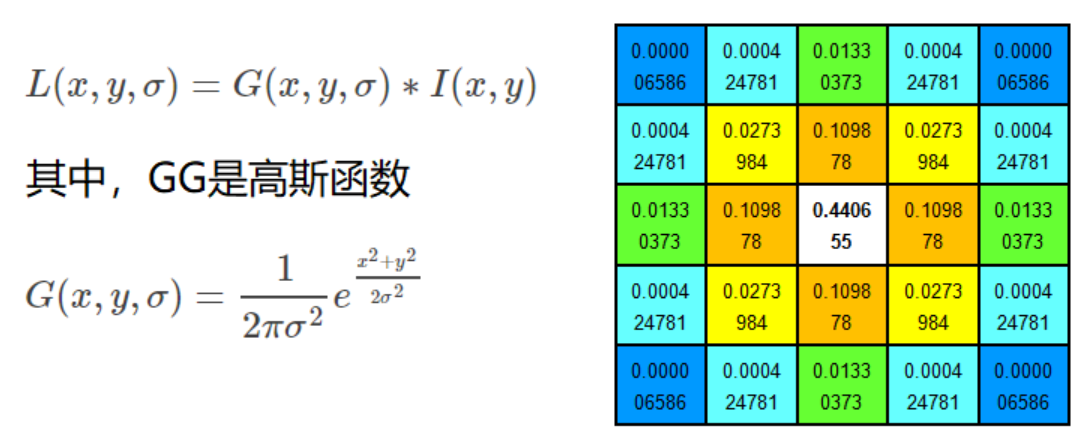
其中，*表示卷积计算。

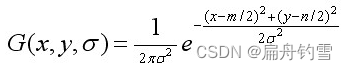
其中，m、n表示高斯模版的维度，(x,y)代表图像像素的位置。$\sigma$为尺度空间因子，$\sigma$值越小表示图像被平滑的越少，相应的尺度就越小。小尺度对应于图像的细节特征，大尺度对应于图像的概貌特征，效果如下图所示，尺度从左到右，从上到下，一次增大。

1.2多分辨率金字塔

• SIFT 第二步就是建立高斯金字塔

尺度空间在实现时，使用高斯金字塔表示，高斯金字塔的构建分为两部分：

1.对图像做不同尺度的高斯模糊

2.对图像做降采样（隔点采样）

图像的金字塔模型是指，将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金子塔的第一层，每次降采样所得到的新图像为金字塔的上一层(每层一张图像)，每个金字塔共n层。金字塔的层数根据图像的原始大小和塔顶图像的大小共同决定。

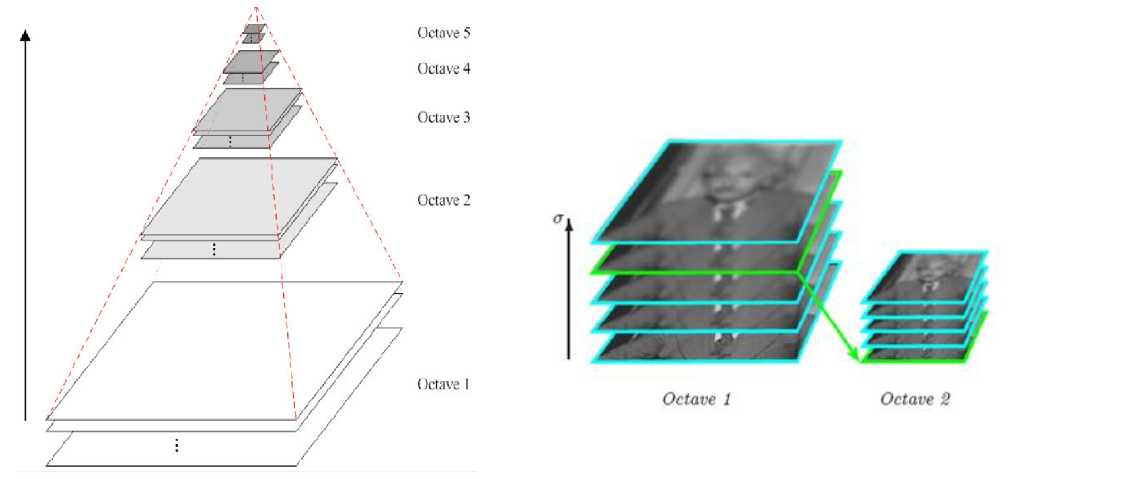
为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如上图所示，将图像金字塔每层的一张图像使用不同参数做高斯模糊，使得金字塔的每层含有多张高斯模糊图像，将金字塔每层多张图像合称为一组(Octave)，金字塔每层只有一组图像，组数和金字塔层数相等，每组含有多层Interval图像。

高斯图像金字塔共o组、s层， 则有：

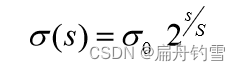
其中，σ表示尺度空间坐标，s表示sub-level层坐标，${\sigma }_0$表示初始尺度，S表示每组层数（一般为3~5）

1.3 高斯差分金字塔（DOG）

SIFT 第三步就是建立DOG高斯差分金字塔

• DoG空间极值检测

为了寻找尺度空间的极值点，每个像素点要和其图像域（同一尺度空间）和尺度域（相邻的尺度空间）的所有相邻点进行比较，当其大于（或者小于）所有相邻点时，该点就是极值点。如下图所示，中间的检测点要和其所在图像的3×3邻域8个像素点，以及其相邻的上下两层的3×3领域18个像素点，共26个像素点进行比较。

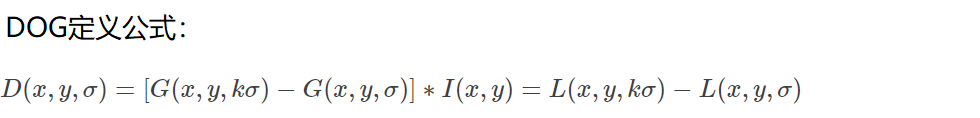
DOG在计算上只需相邻高斯平滑后图像相减，因此简化了计算！

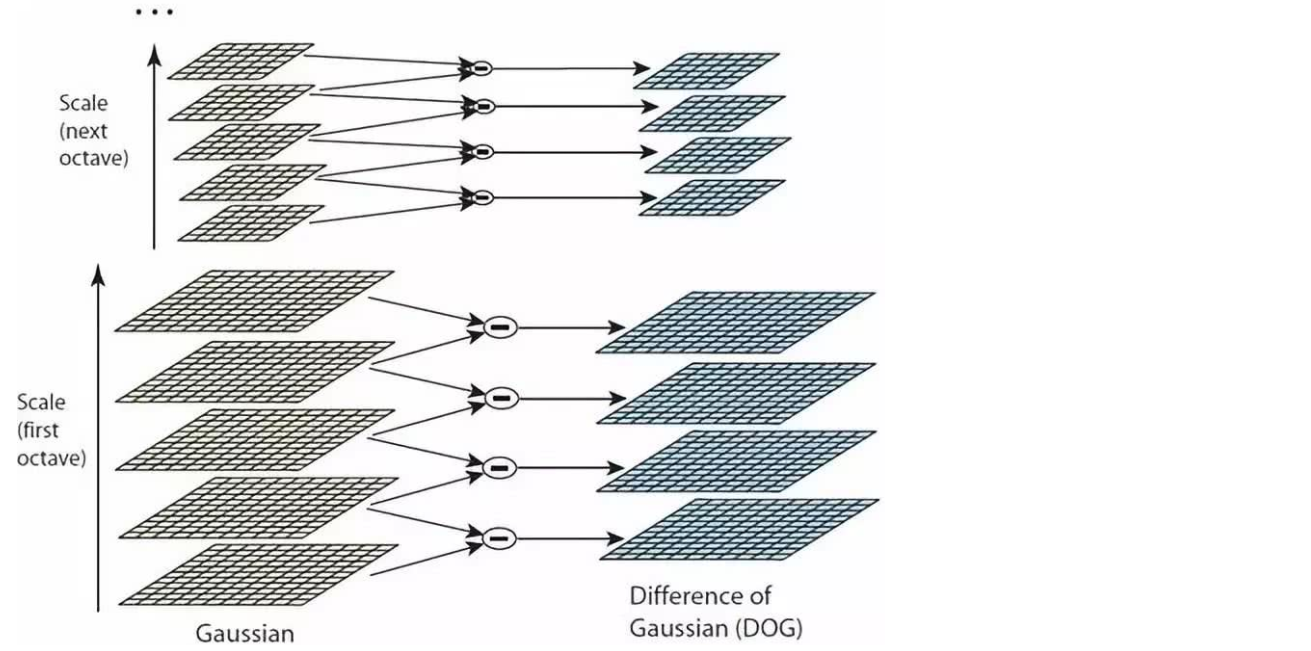
可以通过高斯差分图像看出图像上的像素值变化情况。（如果没有变化，也就没有特征。特征必须是变化尽可能多的点。）DOG图像描绘的是目标的轮廓

1.4 DOG局部极值检测

特征点是由DOG空间的局部极值点组成的。为了寻找DOG函数的极值点，每一个像素点要和它所有的相邻点比较，看其是否比它的图像域和尺度域 的相邻点大或者小。

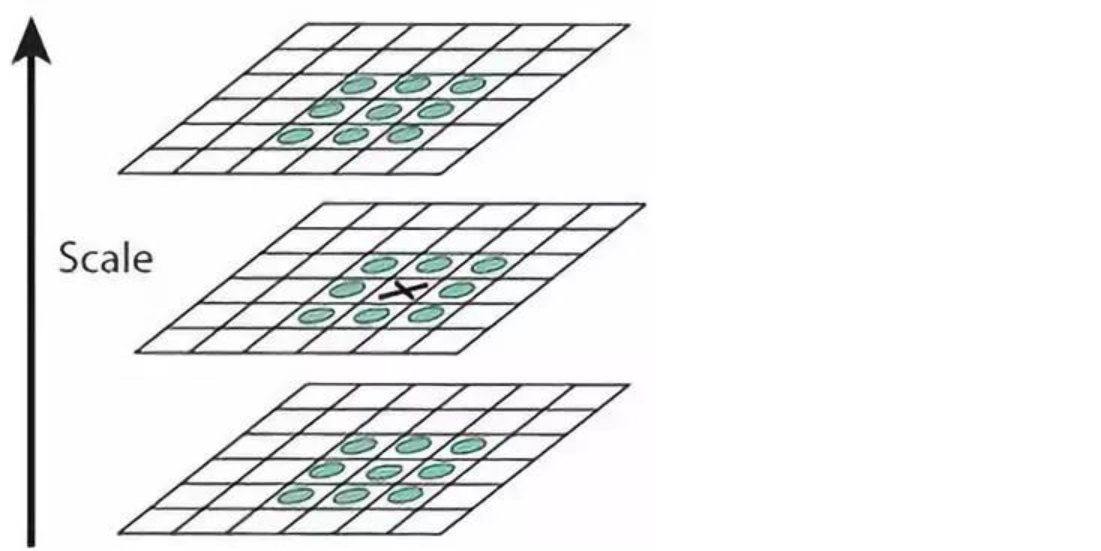
中间的检测点和它同尺度的8个相邻点和上下相邻尺度对应的9×2个 点共26个点比较，以确保在尺度空间和二维图像空间都检测到极值点。

1.5 关键点的精确定位

这些候选关键点是DOG空间的局部极值点，而且这些极值点均为离散的点，精确定位极值点的一种方法是，对尺度空间DoG函数进行曲线拟合，计算其极值点，从而实现关键点的精确定位。

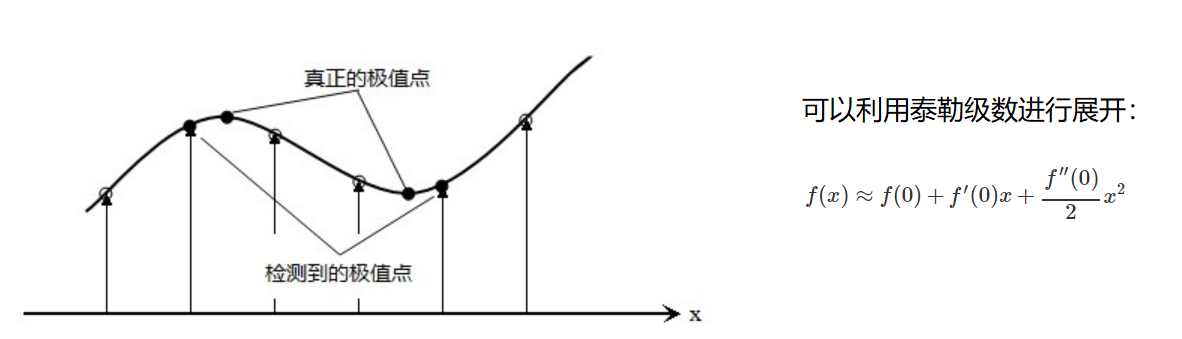求导并让方程等于零，可以得到极值点的偏移量为：

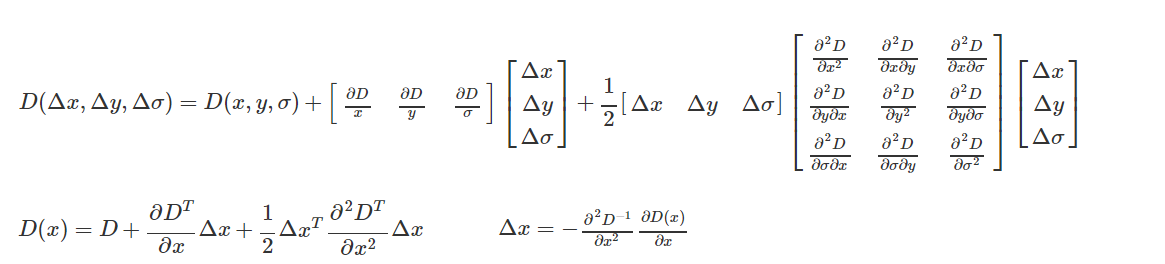
• 消除边界响应

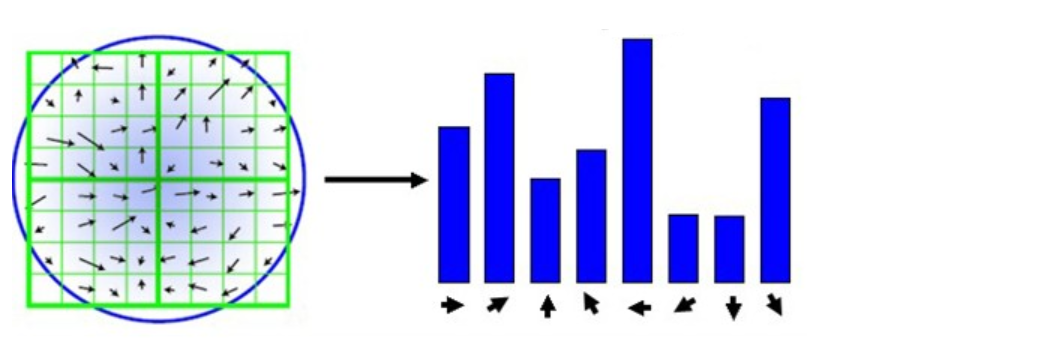
1.6特征点的主方向

每个特征点可以得到三个信息(x,y,σ,θ)，即位置、尺度和方向。具有多个方向的关键点可以被复制成多份，然后将方向值分别赋给复制后的特征点，一个特征点就产生了多个坐标、尺度相等，但是方向不同的特征点。

1.7生成特征描述

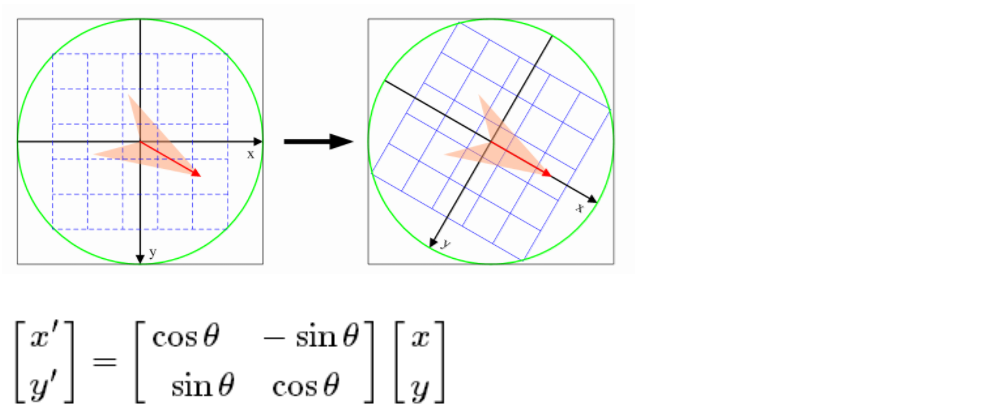
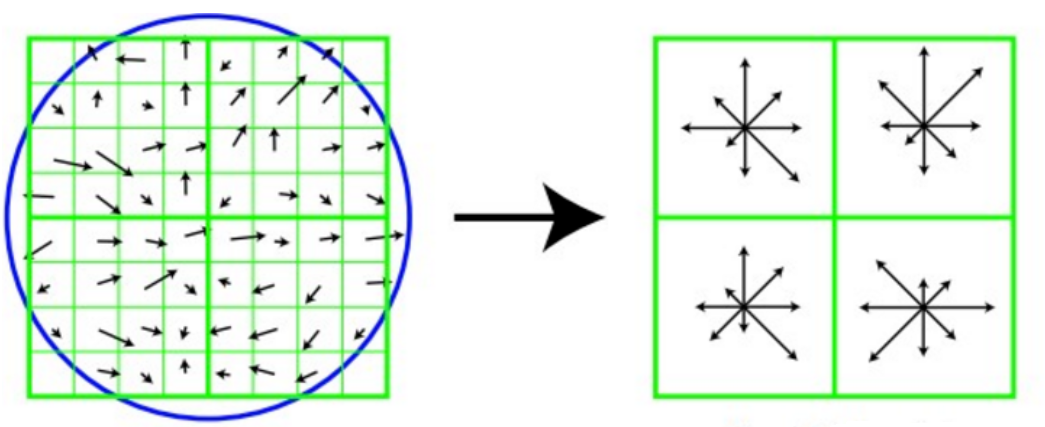
为了保证特征矢量的旋转不变性，要以特征点为中心，在附近邻域内将坐标轴旋转θ角度，即将坐标轴旋转为特征点的主方向。

旋转之后的主方向为中心取8x8的窗口，求每个像素的梯度幅值和方向，箭头方向代表梯度方向，长度代表梯度幅值，然后利用高斯窗口对其进行加权运算，最后在每个4x4的小块上绘制8个方向的梯度直方图，计算每个梯度方向的累加值，即可形成一个种子点，即每个特征的由4个种子点组成，每个种子点有8个方向的向量信息。

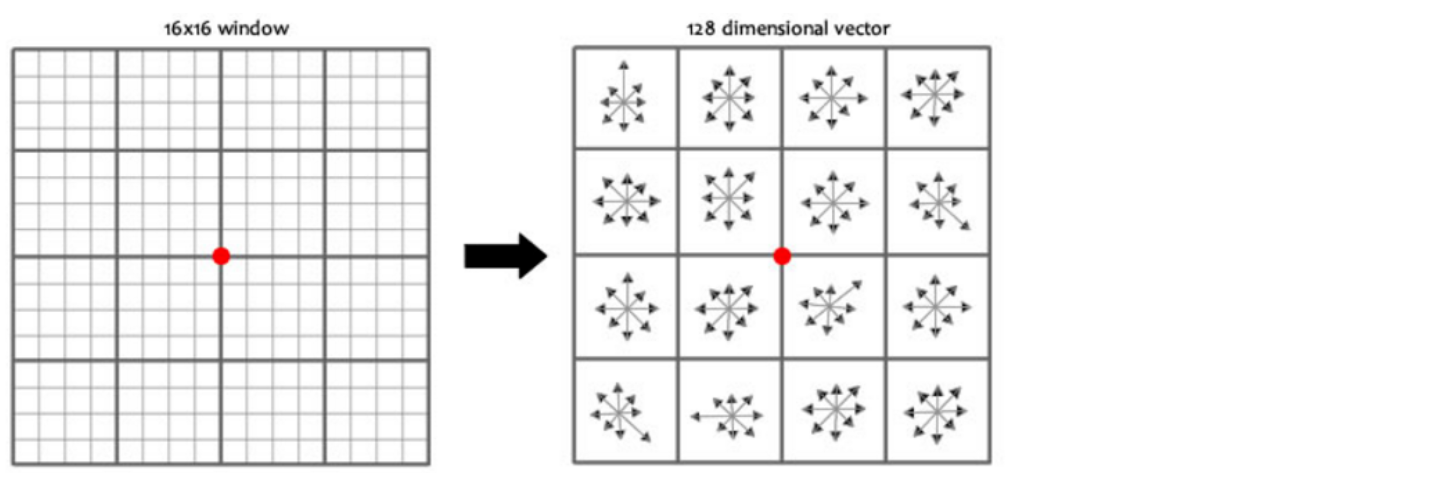
论文中建议对每个关键点使用4x4共16个种子点来描述，这样一个关键点就会产生128维的SIFT特征向量。

2.SIFI关键点检测基于OpenCV实现

• 创建SIFT对象 sift = cv2.xfeatures2d.SIFT_create()
• 进行检测, kp = sift. detect(img, …)
• 绘制关键点, drawKeypoints(gray, kp, img)

 import cv2
import numpy as npimg = cv2.imread('chess.png')gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)# 创建sift对象
# 注意: xfeatures2d是opencv的扩展包中的内容, 需要安装opencv-contrib-python
sift = cv2.xfeatures2d.SIFT_create()# 进行检测
kp = sift.detect(gray)
# print(kp)# 绘制关键点
cv2.drawKeypoints(gray, kp, img)cv2.imshow('img', img)
cv2.waitKey(0)
cv2.destroyAllWindows()

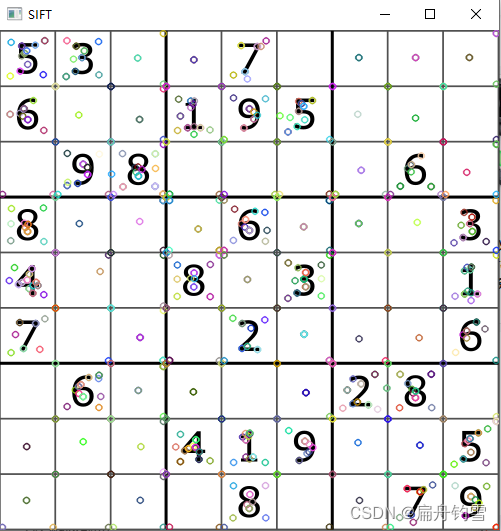
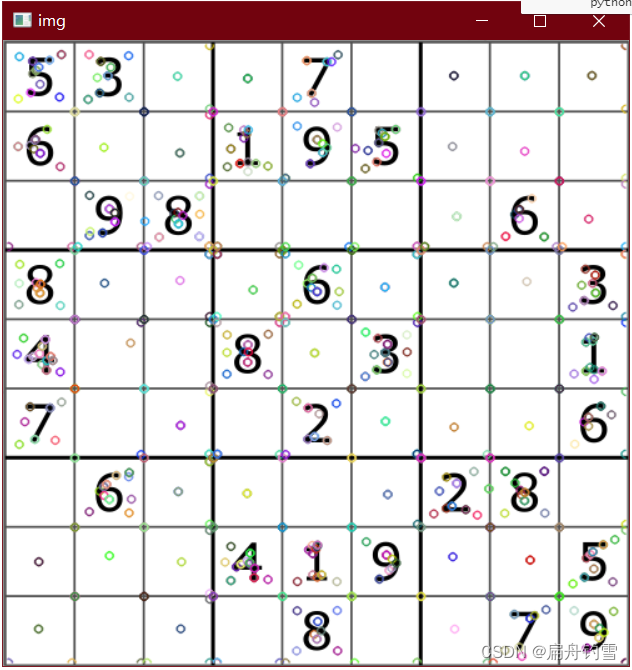
结果如图

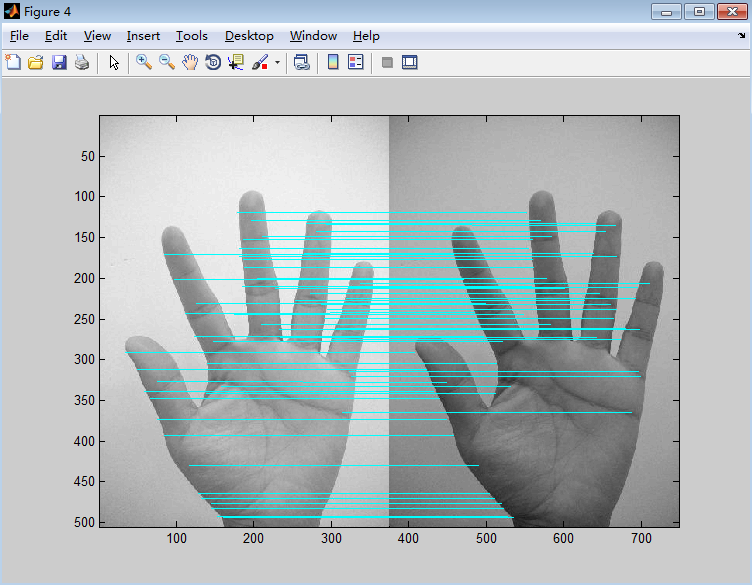
下图为harris 的结果

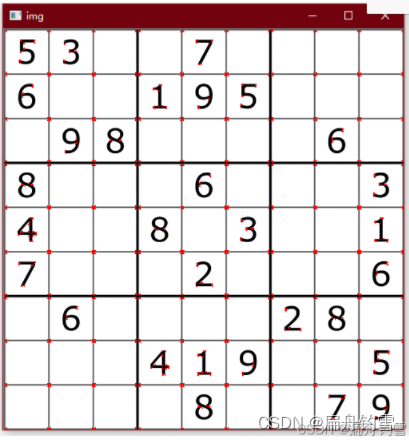
由上面两张图对比可知，SIFT算法匹配出的特征点更多，这是因为SIFT算法具有尺度和旋转不变性，即使两张图大小不一样、角度不一致也不会影响匹配结果，而Harris角点对尺度变化非常敏感，当遇到尺度变化较大时，很多正确特征点无法检测出来。

3.关键点和描述子

关键点: 位置, 大小和方向.

关键点描述子: 记录了关键点周围对其有共享的像素点的一组向量值, 其不受仿射变换, 光照变换等影响.描述子的作用就是进行特征匹配, 在后面进行特征匹配的时候会用上.

代码实现

 import cv2
import numpy as npimg = cv2.imread('chess.png')gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)# 创建sift对象
sift = cv2.xfeatures2d.SIFT_create()# 进行检测
kp = sift.detect(gray)# 检测关键点, 并计算描述子
kp, des = sift.compute(img, kp)
# 或者一步到位, 把关键点和描述子一起检测出来.
kp, des = sift.detectAndCompute(img, None)
# print(kp)
print(des)
print(des.shape)

执行结果

绘制关键点

cv2.drawKeypoints(gray, kp, img)

cv2.imshow(‘img’, img)
cv2.waitKey(0)
cv2.destroyAllWindows()

执行结果