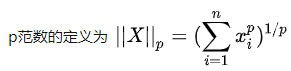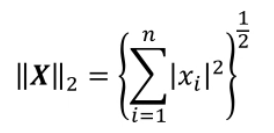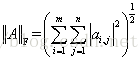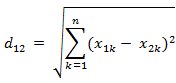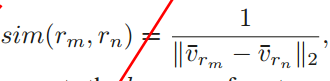SIFI和ORB在尺度缩放、旋转、仿射上的特征点不变实验代码，并比较SIFI和ORB提取特征点的速度

article/2025/9/30 23:02:34

SIFI和ORB在尺度缩放、旋转、仿射上的特征点不变

  • 一、SIFI算法
    • 1.验证旋转不变性
    • 2.验证尺度不变性
    • 3.验证仿射不变性 对原图进行仿射变换并输出
  • 二、ORB算法
    • 1.验证旋转不变性
    • 2.验证尺度不变性
    • 3.验证仿射不变性 对原图进行仿射变换并输出
  • 三、比较SIFT和ORB的尺度旋转，缩放，仿射上运行时间
      • 由此可见，ORB提取特征点的速度比SIFI好

一、SIFI算法

1.验证旋转不变性

import numpy as np
import time
import cv2
from matplotlib import pyplot as pltsift = cv2.xfeatures2d.SIFT_create()
# FLANN 参数设计
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params,search_params)img1 = cv2.imread('1.jpg')
img2 = cv2.imread('2.jpg')
#使用cv2.imread()接口读图像，读进来的是BGR格式以及[0～255]。所以要将img转换为RGB格式，不然后面显示会有色差
img1 = cv2.cvtColor(img1,cv2.COLOR_BGR2RGB)
gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY) #灰度处理图像
#使用cv2.imread()接口读图像，读进来的是BGR格式以及[0～255]。所以要将img转换为RGB格式，不然后面显示会有色差
img2 = cv2.cvtColor(img2,cv2.COLOR_BGR2RGB)
gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)start11 = time.time()
kp1, des1 = sift.detectAndCompute(img1,None)#des是描述符
kp2, des2 = sift.detectAndCompute(img2,None)
end11 = time.time()print (des1.shape) #描述符数组维度 
print(len(kp1))   #关键点个数
print (des2.shape) #描述符数组维度 
print(len(kp2))   #关键点个数print(img1.shape)
print(img2.shape)
hmerge = np.hstack((img1, img2)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('original')
plt.axis('off')
plt.show()hmerge = np.hstack((gray1, gray2)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge,cmap='gray')
plt.title('gray')
plt.axis('off')
plt.show()img3 = cv2.drawKeypoints(img1,kp1,img1,color=(255,0,255))
img4 = cv2.drawKeypoints(img2,kp2,img2,color=(255,0,255))hmerge = np.hstack((img3, img4)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('keypoint')
plt.axis('off')
plt.show()matches = flann.knnMatch(des1,des2,k=2)
matchesMask = [[0,0] for i in range(len(matches))]good = []
for m,n in matches:if m.distance < 0.7*n.distance:good.append([m])img5 = cv2.drawMatchesKnn(img1,kp1,img2,kp2,good,None,flags=2)plt.figure(num=1,figsize=(16,16))
plt.imshow(img5)
plt.title('SIFT_rotation')
plt.axis('off')
plt.show()

(1085, 128)
1085
(1089, 128)
1089
(400, 600, 3)
(400, 600, 3)

在这里插入图片描述

2.验证尺度不变性

img1 = cv2.imread("1.jpg")
img2 = cv2.imread("3.jpg")
img1 = cv2.cvtColor(img1,cv2.COLOR_BGR2RGB)
img2 = cv2.cvtColor(img2,cv2.COLOR_BGR2RGB)
print(img1.shape)
print(img2.shape)
plt.figure(num=1,figsize=(12,12))
plt.imshow(img1,cmap='gray')
plt.title('original_img1')
plt.axis('off')
plt.show()
plt.figure(num=1,figsize=(12,12))
plt.imshow(img2,cmap='gray')
plt.title('original_img2')
plt.axis('off')
plt.show()#灰度化处理，打印描述符数组维度和关键点个数
gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)
gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)start12 = time.time()
kp1, des1 = sift.detectAndCompute(img1,None)
kp2, des2 = sift.detectAndCompute(img2,None)
end12 = time.time()print (des1.shape) #描述符数组维度 
print(len(kp1))   #关键点个数
print (des1.shape) #描述符数组维度 
print(len(kp2))   #关键点个数plt.figure(num=1,figsize=(12,12))
plt.imshow(gray1,cmap='gray')
plt.title('gray1')
plt.axis('off')
plt.show()
plt.figure(num=1,figsize=(12,12))
plt.imshow(gray2,cmap='gray')
plt.title('gray2')
plt.axis('off')
plt.show()img3 = cv2.drawKeypoints(img1,kp1,img1,color=(255,0,255))
img4 = cv2.drawKeypoints(img2,kp2,img2,color=(255,0,255))plt.figure(num=1,figsize=(12,12))
plt.imshow(img3)
plt.title('keypoint_img3')
plt.axis('off')
plt.show()
plt.figure(num=1,figsize=(12,12))
plt.imshow(img4)
plt.title('keypoint_img4')
plt.axis('off')
plt.show()matches = flann.knnMatch(des1,des2,k=2)
matchesMask = [[0,0] for i in range(len(matches))]good = []
for m,n in matches:if m.distance < 0.7*n.distance:good.append([m])img5 = cv2.drawMatchesKnn(img1,kp1,img2,kp2,good,None,flags=2)plt.figure(num=1,figsize=(16,16))
plt.imshow(img5)
plt.title('SIFT_size')
plt.axis('off')
plt.show()

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.验证仿射不变性 对原图进行仿射变换并输出

img = cv2.imread('1.jpg')
img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
rows, cols, ch = img.shapepts1 = np.float32([[0, 0], [cols - 1, 0], [0, rows - 1]])
pts2 = np.float32([[cols * 0.2, rows * 0.1], [cols * 0.9, rows * 0.2], [cols * 0.1, rows * 0.9]])M = cv2.getAffineTransform(pts1, pts2)
dst = cv2.warpAffine(img, M, (cols, rows))
plt.figure(num=1,figsize=(16,16))
plt.imshow(dst)
plt.title('affine_img')
plt.axis('off')
plt.show()print(img.shape)
print(dst.shape)
hmerge = np.hstack((img, dst))  # 两张图片横向合并（便于对比显示）
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('original')
plt.axis('off')
plt.show()gray1 = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #灰度处理图像
gray2 = cv2.cvtColor(dst, cv2.COLOR_BGR2GRAY) #灰度处理图像start13 = time.time()
kp1, des1 = sift.detectAndCompute(img,None)#des是描述符
kp2, des2 = sift.detectAndCompute(dst,None)#des是描述符
end13 = time.time()print (des1.shape) #描述符数组维度 
print(len(kp1))   #关键点个数
print (des2.shape) #描述符数组维度 
print(len(kp2))   #关键点个数hmerge = np.hstack((gray1, gray2))  # 两张图片横向合并（便于对比显示）
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge,cmap='gray')
plt.title('gray')
plt.axis('off')
plt.show()img3 = cv2.drawKeypoints(img,kp1,img,color=(255,0,255))
img4 = cv2.drawKeypoints(dst,kp2,dst,color=(255,0,255))hmerge = np.hstack((img3, img4)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('keypoint')
plt.axis('off')
plt.show()matches = flann.knnMatch(des1,des2,k=2)
matchesMask = [[0,0] for i in range(len(matches))]good = []
for m,n in matches:if m.distance < 0.7*n.distance:good.append([m])img5 = cv2.drawMatchesKnn(img,kp1,dst,kp2,good,None,flags=2)plt.figure(num=1,figsize=(16,16))
plt.imshow(img5)
plt.title('SIFT_affine')
plt.axis('off')
plt.show()

在这里插入图片描述

二、ORB算法

1.验证旋转不变性

import numpy as np
import cv2
from matplotlib import pyplot as pltorb=cv2.ORB_create()
# FLANN 参数设计
FLANN_INDEX_KDTREE = 0
index_params = dict(algorithm = FLANN_INDEX_KDTREE, trees = 5)
search_params = dict(checks=50)
flann = cv2.FlannBasedMatcher(index_params,search_params)img1 = cv2.imread('1.jpg')
#使用cv2.imread()接口读图像，读进来的是BGR格式以及[0～255]。所以要将img转换为RGB格式，不然后面显示会有色差
img1 = cv2.cvtColor(img1,cv2.COLOR_BGR2RGB)
gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY) #灰度处理图像img2 = cv2.imread('2.jpg')
#使用cv2.imread()接口读图像，读进来的是BGR格式以及[0～255]。所以要将img转换为RGB格式，不然后面显示会有色差
img2 = cv2.cvtColor(img2,cv2.COLOR_BGR2RGB)
gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)start21 = time.time()
kp1, des1 = orb.detectAndCompute(img1,None)#des是描述符
kp2, des2 = orb.detectAndCompute(img2,None)
end21 = time.time()print (des1.shape) #描述符数组维度 
print(len(kp1))   #关键点个数
print (des2.shape) #描述符数组维度 
print(len(kp2))   #关键点个数print(img1.shape)
print(img2.shape)
hmerge = np.hstack((img1, img2)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('original')
plt.axis('off')
plt.show()hmerge = np.hstack((gray1, gray2)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge,cmap='gray')
plt.title('gray')
plt.axis('off')
plt.show()img3 = cv2.drawKeypoints(img1,kp1,img1,color=(255,0,255))
img4 = cv2.drawKeypoints(img2,kp2,img2,color=(255,0,255))hmerge = np.hstack((img3, img4)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('keypoint')
plt.axis('off')
plt.show()# 获得一个暴力匹配器的对象
bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)
# 利用匹配器 匹配两个描述符的相近成都
maches = bf.match(des1,des2)
# 按照相近程度 进行排序
maches = sorted(maches, key=lambda x: x.distance)
# 画出匹配项
img5 = cv2.drawMatches(img1,kp1,img2,kp2, maches[:], None, flags=2)plt.figure(num=1,figsize=(16,16))
plt.imshow(img5)
plt.title('ORB_rotation')
plt.axis('off')
plt.show()

运行结果：
在这里插入图片描述

2.验证尺度不变性

img1 = cv2.imread("1.jpg")
img2 = cv2.imread("3.jpg")
img1 = cv2.cvtColor(img1,cv2.COLOR_BGR2RGB)
img2 = cv2.cvtColor(img2,cv2.COLOR_BGR2RGB)
print(img1.shape)
print(img2.shape)
plt.figure(num=1,figsize=(12,12))
plt.imshow(img1,cmap='gray')
plt.title('original_img1')
plt.axis('off')
plt.show()
plt.figure(num=1,figsize=(12,12))
plt.imshow(img2,cmap='gray')
plt.title('original_img2')
plt.axis('off')
plt.show()gray1 = cv2.cvtColor(img1, cv2.COLOR_BGR2GRAY)gray2 = cv2.cvtColor(img2, cv2.COLOR_BGR2GRAY)start22 = time.time()
kp1, des1 = orb.detectAndCompute(img1,None)
kp2, des2 = orb.detectAndCompute(img2,None)
end22 = time.time()print (des1.shape) #描述符数组维度 
print(len(kp1))   #关键点个数
print (des1.shape) #描述符数组维度 
print(len(kp2))   #关键点个数plt.figure(num=1,figsize=(12,12))
plt.imshow(gray1,cmap='gray')
plt.title('gray1')
plt.axis('off')
plt.show()
plt.figure(num=1,figsize=(12,12))
plt.imshow(gray2,cmap='gray')
plt.title('gray2')
plt.axis('off')
plt.show()img3 = cv2.drawKeypoints(img1,kp1,img1,color=(255,0,255))
img4 = cv2.drawKeypoints(img2,kp2,img2,color=(255,0,255))plt.figure(num=1,figsize=(12,12))
plt.imshow(img3)
plt.title('keypoint_img3')
plt.axis('off')
plt.show()
plt.figure(num=1,figsize=(12,12))
plt.imshow(img4)
plt.title('keypoint_img4')
plt.axis('off')
plt.show()# 获得一个暴力匹配器的对象
bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)
# 利用匹配器 匹配两个描述符的相近成都
maches = bf.match(des1,des2)
# 按照相近程度 进行排序
maches = sorted(maches, key=lambda x: x.distance)
# 画出匹配项
img5 = cv2.drawMatches(img1,kp1,img2,kp2, maches[: 30], None, flags=2)plt.figure(num=1,figsize=(16,16))
plt.imshow(img5)
plt.title('ORB_size')
plt.axis('off')
plt.show()

运行结果：
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

3.验证仿射不变性 对原图进行仿射变换并输出

img = cv2.imread('1.jpg')
img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)
rows, cols, ch = img.shapepts1 = np.float32([[0, 0], [cols - 1, 0], [0, rows - 1]])
pts2 = np.float32([[cols * 0.2, rows * 0.1], [cols * 0.9, rows * 0.2], [cols * 0.1, rows * 0.9]])M = cv2.getAffineTransform(pts1, pts2)
dst = cv2.warpAffine(img, M, (cols, rows))
plt.figure(num=1,figsize=(16,16))
plt.imshow(dst)
plt.title('affine_img')
plt.axis('off')
plt.show()print(img.shape)
print(dst.shape)
hmerge = np.hstack((img, dst))  # 两张图片横向合并（便于对比显示）
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('original')
plt.axis('off')
plt.show()gray1 = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) #灰度处理图像
gray2 = cv2.cvtColor(dst, cv2.COLOR_BGR2GRAY) #灰度处理图像start23 = time.time()
kp1, des1 = orb.detectAndCompute(img,None)#des是描述符
kp2, des2 = orb.detectAndCompute(dst,None)#des是描述符
end23 = time.time()print (des1.shape) #描述符数组维度 
print(len(kp1))   #关键点个数
print (des2.shape) #描述符数组维度 
print(len(kp2))   #关键点个数hmerge = np.hstack((gray1, gray2))  # 两张图片横向合并（便于对比显示）
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge,cmap='gray')
plt.title('gray')
plt.axis('off')
plt.show()img3 = cv2.drawKeypoints(img,kp1,img,color=(255,0,255))
img4 = cv2.drawKeypoints(dst,kp2,dst,color=(255,0,255))hmerge = np.hstack((img3, img4)) #水平拼接
plt.figure(num=1,figsize=(16,16))
plt.imshow(hmerge)
plt.title('keypoint')
plt.axis('off')
plt.show()# 获得一个暴力匹配器的对象
bf = cv2.BFMatcher(cv2.NORM_HAMMING, crossCheck=True)
# 利用匹配器 匹配两个描述符的相近成都
maches = bf.match(des1,des2)
# 按照相近程度 进行排序
maches = sorted(maches, key=lambda x: x.distance)
# 画出匹配项
img5 = cv2.drawMatches(img,kp1,dst,kp2, maches[:], None, flags=2)plt.figure(num=1,figsize=(16,16))
plt.imshow(img5)
plt.title('ORB_affine')
plt.axis('off')
plt.show()

运行结果：
在这里插入图片描述

三、比较SIFT和ORB的尺度旋转，缩放，仿射上运行时间

print("SIFI的旋转的体征点提取速度",end11-start11)
print("SIFI的缩放的体征点提取速度",end12-start12)
print("SIFI的仿射的体征点提取速度",end13-start13)print("ORB的旋转的体征点提取速度",end21-start21)
print("ORB的缩放的体征点提取速度",end22-start22)
print("ORB的仿射的体征点提取速度",end23-start23)

SIFI的旋转的体征点提取速度 0.09574317932128906
SIFI的缩放的体征点提取速度 0.06183433532714844
SIFI的仿射的体征点提取速度 0.09873533248901367
ORB的旋转的体征点提取速度 0.012612581253051758
ORB的缩放的体征点提取速度 0.008951902389526367
ORB的仿射的体征点提取速度 0.011967182159423828

由此可见，ORB提取特征点的速度比SIFI好


http://chatgpt.dhexx.cn/article/QDba0UKM.shtml

相关文章

向量范数简述

向量范数简述

向量范数&#xff1a;表征在向量空间中向量的大小 一般表示&#xff1a;,其中X是n维向量&#xff0c;一般如果省略下面的p且无特别说明的话&#xff0c;指的就是2范数&#xff0c;也叫欧几里得范数。对向量来说&#xff0c;就是指向量的模。 常用的向量范数&#xff1a; 0范…
阅读更多...
欧几里得范数/欧几里得距离(L2范数)

欧几里得范数/欧几里得距离(L2范数)

首先m维空间的概念: Rm的距离结构: 2维平面空间: m维空间: 范形空间距离 n维矢量空间中的元素X的Lp范数: 其中X是一连串的向量 最常用的是L2范数: 本质是一个距离概念 参考:《数学分析》
阅读更多...
概念理解_L2范数（欧几里得范数）

概念理解_L2范数（欧几里得范数）

L2范数 L2范数、欧几里得范数一些概念。 首先&#xff0c;明确一点&#xff0c;常用到的几个概念&#xff0c;含义相同。 欧几里得范数&#xff08;Euclidean norm&#xff09; 欧式长度 L2 范数 L2距离 Euclidean norm Euclidean length L2 norm L2 distance norm 对于一…
阅读更多...
0范数，1范数，欧几里得范数等范数总结

0范数，1范数，欧几里得范数等范数总结

以下分别列举常用的向量范数和矩阵范数的定义。 向量范数 1-范数&#xff1a; 即向量元素绝对值之和&#xff0c;matlab调用函数norm(x, 1) 。 2-范数&#xff1a; Euclid范数&#xff08;欧几里得范数&#xff0c;常用计算向量长度&#xff09;&#xff0c;即向量元素绝对值…
阅读更多...
范数、正则化、归一化、标准化

范数、正则化、归一化、标准化

在总结正则化&#xff08;Regularization&#xff09;之前&#xff0c;我们先谈一谈正则化是什么&#xff0c;为什么要正则化。 个人认为正则化这个字眼有点太过抽象和宽泛&#xff0c;其实正则化的本质很简单&#xff0c;就是对某一问题加以先验的限制或约束以达到某种特定目的…
阅读更多...
常见向量范数和矩阵范数

常见向量范数和矩阵范数

1、向量范数 1-范数&#xff1a;&#xff0c;即向量元素绝对值之和&#xff0c;matlab调用函数norm(x, 1) 。 2-范数&#xff1a;&#xff0c;Euclid范数&#xff08;欧几里得范数&#xff0c;常用计算向量长度&#xff09;&#xff0c;即向量元素绝对值的平方和再开方&#xf…
阅读更多...
欧氏距离,l2范数,l2-loss,l2正则化

欧氏距离,l2范数,l2-loss,l2正则化

欧式距离,l2范数,l2-loss,l2正则化 1.欧氏距离2.L2范数范数计算公式L1范数L2范数在机器学习方面的区别为什么L2范数可以防止过拟合? 3.L2-Loss4.L2正则化正则化L2正则化 参考文献 1.欧氏距离 距离度量&#xff08;Distance&#xff09;用于衡量个体在空间上存在的距离&#x…
阅读更多...
pytorch求范数函数——torch.norm

pytorch求范数函数——torch.norm

torch.norm(input, pfro, dimNone, keepdimFalse, outNone, dtypeNone) 返回所给定tensor的矩阵范数或向量范数,所谓范数也就是把一个高纬度的东西,压缩成为一个大于等于零的数,用以估算这里东西的大小(幅度) 参数&#xff1a; input&#xff1a;输入tensorp (int, float, i…
阅读更多...
来自知乎的范数理解

来自知乎的范数理解

以下分别列举常用的向量范数和矩阵范数的定义。 向量范数 1-范数&#xff1a; &#xff0c;即向量元素绝对值之和&#xff0c;matlab调用函数norm(x, 1) 。 2-范数&#xff1a; &#xff0c;Euclid范数&#xff08;欧几里得范数&#xff0c;常用计算向量长度&#xff09;&…
阅读更多...
16.1 几何空间

16.1 几何空间

文章目录 1 欧几里得范数2 距离3 标准内积5 夹角与正交6 叉乘7 平行四边形法则8 欧几里得运动 几何空间是用线性代数解决几何问题的一类空间&#xff0c;这是线性代数学习绕不过去的槛。几何空间&#xff0c;学习起来我觉得吧&#xff0c;主要是三个点&#xff1a;内积、长度、…
阅读更多...
常见向量范数和矩阵范数及其MATLAB实现

常见向量范数和矩阵范数及其MATLAB实现

参考 常见向量范数和矩阵范数及其MATLAB实现 - 云社区 - 腾讯云 1、向量范数 1-范数&#xff1a;&#xff0c;即向量元素绝对值之和&#xff0c;matlab调用函数norm(x, 1) 。 2-范数&#xff1a;&#xff0c;Euclid范数&#xff08;欧几里得范数&#xff0c;常用计算向量长度…
阅读更多...
MATLAB 欧几里得算法

MATLAB 欧几里得算法

MATLAB 欧几里得算法以及扩展欧几里得算法 前言一、Euclid算法二、Code1.引入库2.读入数据 前言 提示&#xff1a;在线性代数或高等代数中以熟悉求两个多项式最大公因子 一、Euclid算法 输入两个多项式 g(x) , h(x) ∈ F(x),满足 deg g(x) ≥ deg h(x) , 且 g(x) ≠ 0, 二、…
阅读更多...
【 MATLAB 】norm ( Vector and matrix norms )（向量范数以及矩阵范数）

【 MATLAB 】norm ( Vector and matrix norms )（向量范数以及矩阵范数）

norm Vector and matrix norms Syntax n norm(v) n norm(v,p) n norm(X) n norm(X,p) n norm(X,fro) Description n norm&#xff08;v&#xff09;返回向量v的欧几里德范数。该范数也称为2范数&#xff0c;向量幅度或欧几里德长度。 n norm&#xff08;v&#…
阅读更多...
向量范数

向量范数

向量范数的定义如下&#xff1a; 若实值函数&#xff08;n维向量空间向一维向量空间的映射&#xff09;&#xff1a;满足下列条件&#xff1a; &#xff08;1&#xff09;&#xff0c;&#xff1b;当且仅当&#xff1b; &#xff08;2&#xff09;&#xff0c;&#xff0c;&…
阅读更多...
向量和矩阵的各种范数

向量和矩阵的各种范数

向量和矩阵的各种范数 一、向量的范数 首先定义一个向量为&#xff1a;a[-5&#xff0c;6&#xff0c;8, -10] 1.1 向量的1范数 向量的1范数即&#xff1a;向量的各个元素的绝对值之和&#xff0c;上述向量a的1范数结果就是&#xff1a;29&#xff0c;MATLAB代码实现为&…
阅读更多...
欧几里得范数

欧几里得范数

原文链接 点击打开链接 1 范数 向量的范数可以简单形象的理解为向量的长度&#xff0c;或者向量到零点的距离&#xff0c;或者相应的两个点之间的距离。 2 距离 欧式距离&#xff08;对应L2范数&#xff09;&#xff1a;最常见的两点之间或多点之间的距离表示法&#xff0c;…
阅读更多...
p-范数（2-范数 即 欧几里得范数）

p-范数（2-范数 即 欧几里得范数）

规范化矩阵 p-范数定义vecnorm和normvecnorm应用 废了废了&#xff0c;2016版本用不起vecnormnormnorm规范化矩阵 p-范数定义 常见 1-范数、2-范数&#xff08;欧几里得范数&#xff09; vecnorm和norm vecnorm 应用 计算欧式距离别再傻憨憨地去背两点之间的距离公式了&am…
阅读更多...
L2范数-欧几里得范数

L2范数-欧几里得范数

L1范数 L1范数是指向量中各个元素绝对值之和 L2范数 L2范数、欧几里得范数一些概念。 首先&#xff0c;明确一点&#xff0c;常用到的几个概念&#xff0c;含义相同。 欧几里得范数&#xff08;Euclidean norm&#xff09; 欧式长度 L2 范数 L2距离 Euclidean norm Eucl…
阅读更多...
欧几里得范数（L2范数）

欧几里得范数（L2范数）

L1范数和L2范数我们应该经常接触&#xff0c;但是欧几里得范数可能有些人听着会有些陌生&#xff0c;乍一看以为是多么难的东西&#xff0c;其实欧几里得范数就是L2范数&#xff0c;只是叫法不同而已。 L1范数 L1范数是指向量中各个元素绝对值之和。 L2范数&#xff08;欧几…
阅读更多...
SVM算法的介绍

SVM算法的介绍

一、SVM算法的介绍 1.什么是SVM算法&#xff1f; SVM&#xff08;Support Vector Machine&#xff09;是一种常见的监督学习算法&#xff0c;用于进行二分类或多分类任务。它的主要思想是找到一个最优的超平面&#xff0c;将不同类别的样本分隔开。 超平面最大间隔介绍&#…
阅读更多...
推荐文章

Copyright @ 2022~2023