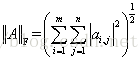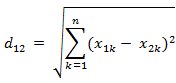来自知乎的范数理解

article/2025/10/1 0:40:26

以下分别列举常用的向量范数和矩阵范数的定义。

向量范数

1-范数：

$||x||_1 = \sum_{i=1}^N|x_i|$ ，即向量元素绝对值之和，matlab调用函数norm(x, 1) 。

2-范数：

$||\textbf{x}||_2 =\sqrt{\sum_{i=1}^Nx_i^2}$ ，Euclid范数（欧几里得范数，常用计算向量长度），即向量元素绝对值的平方和再开方，matlab调用函数norm(x, 2)。

$\infty$ -范数： $||\textbf{x}||_\infty = \max_{i}|x_i|$ ，即所有向量元素绝对值中的最大值，matlab调用函数norm(x, inf)。

$-\infty$ -范数： $||\textbf{x}||_{-\infty}=\min_i|x_i|$

，即所有向量元素绝对值中的最小值，matlab调用函数norm(x, -inf)。

p-范数： $||\textbf{x}||_p = (\sum_{i=1}^N|x_i|^p)^{\frac{1}{p}}$
，即向量元素绝对值的p次方和的1/p次幂，matlab调用函数norm(x, p)。

矩阵范数

1-范数： $||A||_1 = \max_j\sum_{i=1}^m|a_{i,j}|$
，列和范数，即所有矩阵列向量绝对值之和的最大值，matlab调用函数norm(A, 1)。

2-范数： $||A||_2 = \sqrt{\lambda_1}$ ， $\lambda<br/>$ 为 $A^TA$ 的最大特征值。

，谱范数，即A'A矩阵的最大特征值的开平方。matlab调用函数norm(x, 2)。

$\infty$ -范数： $||A||_\infty = \max_i\sum_{j=1}^N|a_{i,j}|$

，行和范数，即所有矩阵行向量绝对值之和的最大值，matlab调用函数norm(A, inf)。

F-范数： $||A||_F=\left(\sum_{i=1}^m\sum_{j=1}^n|a_{i,j}|^2\right)^{\frac{1}{2}}$

，Frobenius范数，即矩阵元素绝对值的平方和再开平方，matlab调用函数norm(A, ’fro‘)。

核范数： $||A||_* = \sum_{i=1}^{n}\lambda_i, \lambda_i$ 是A的奇异值。

作者：魏通
链接：https://www.zhihu.com/question/20473040/answer/102907063
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

作者：JI Weiwei
链接：https://www.zhihu.com/question/20473040/answer/25599737
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

你是问向量范数还是矩阵范数？
要更好的理解范数，就要从函数、几何与矩阵的角度去理解，我尽量讲的通俗一些。
我们都知道，函数与几何图形往往是有对应的关系，这个很好想象，特别是在三维以下的空间内，函数是几何图像的数学概括，而几何图像是函数的高度形象化，比如一个函数对应几何空间上若干点组成的图形。
但当函数与几何超出三维空间时，就难以获得较好的想象，于是就有了映射的概念，映射表达的就是一个集合通过某种关系转为另外一个集合。通常数学书是先说映射，然后再讨论函数，这是因为函数是映射的一个特例。
为了更好的在数学上表达这种映射关系，（这里特指线性关系）于是就引进了矩阵。这里的矩阵就是表征上述空间映射的线性关系。而通过向量来表示上述映射中所说的这个集合，而我们通常所说的基，就是这个集合的最一般关系。于是，我们可以这样理解，一个集合（向量），通过一种映射关系（矩阵），得到另外一个几何（另外一个向量）。
那么向量的范数，就是表示这个原有集合的大小。
而矩阵的范数，就是表示这个变化过程的大小的一个度量。

那么说到具体几几范数，其不过是定义不同，一个矩阵范数往往由一个向量范数引出，我们称之为算子范数，其物理意义都如我上述所述。

以上符合知乎回答问题的方式。

接下来用百度回答方式：

0范数，向量中非零元素的个数。

1范数，为绝对值之和。

2范数，就是通常意义上的模。

x 的 0 范数：x 到零点的汉明距离

x 的 1 范数：x 到零点的曼哈顿距离

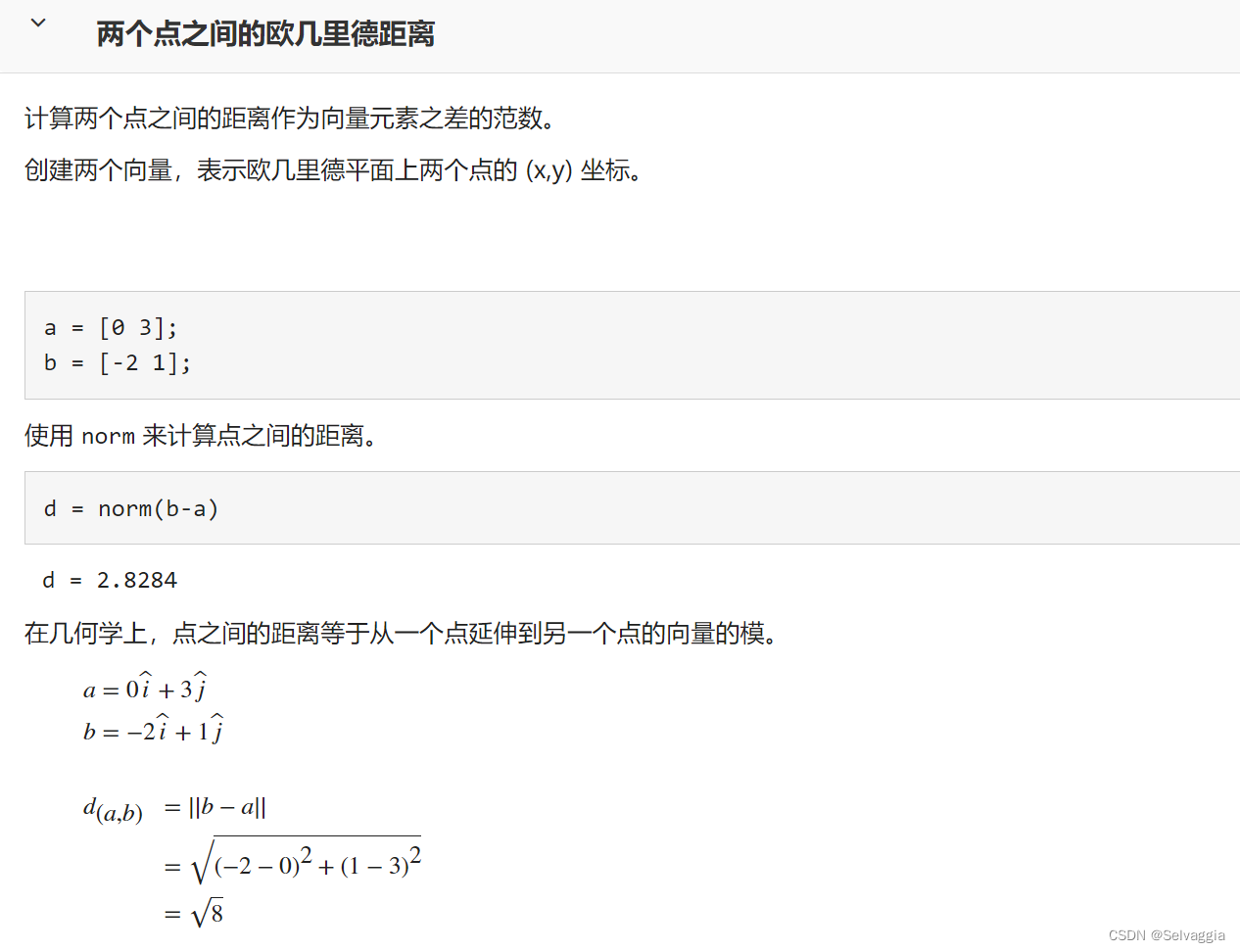
x 的 2 范数：x 到零点的欧氏距离

...

x 的 n 范数：x 到零点的 n 阶闵氏距离

x 的无穷范数：x 到零点的切比雪夫距离